Ôn tập Đại số 10 - Chương VI: Góc – cung lượng giác công thức lượng giác (Phần A)

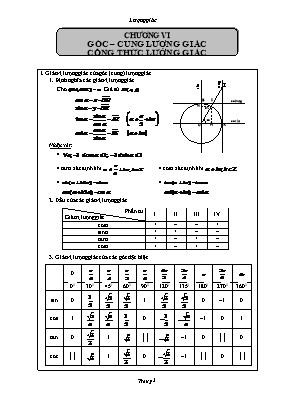
CHƯƠNG VI
GÓC – CUNG LƯỢNG GIÁC
CÔNG THỨC LƯỢNG GIÁC
I. Giá trị lượng giác của góc (cung) lượng giác
cosin
O
cotang
 sin 
tang
H
A
M
K
B
S
a
T
	1. Định nghĩa các giá trị lượng giác
	Cho . Giả sử .
	Nhận xét: 
	· 
	· tana xác định khi 	· cota xác định khi 
	· 	· 
	2. Dấu của các giá trị lượng giác
Phần tư
Giá trị lượng giác
I
II
III
IV
cosa
+
–
–
+
sina
+
+
–
–
tana
+
–
+
–
cota
+
–
+
–
	3. Giá trị lượng giác của các góc đặc biệt
0
00
300
450
600
900
1200
1350
1800
2700
3600
sin
0
1
0
–1
0
cos
1
0
–1
0
1
tan
0
1
–1
0
0
cot
1
0
–1
0
	4. Hệ thức cơ bản:
; 	; 
	5. Giá trị lượng giác của các góc có liên quan đặc biệt
Góc đối nhau
Góc bù nhau
Góc phụ nhau
Góc hơn kém 
Góc hơn kém 
II. Công thức lượng giác
	1. Công thức cộng
	Hệ quả: 
	2. Công thức nhân đôi
Công thức hạ bậc
Công thức nhân ba (*)
	3. Công thức biến đổi tổng thành tích
	4. Công thức biến đổi tích thành tổng
VẤN ĐỀ 1: Dấu của các giá trị lượng giác
	Để xác định dấu của các giá trị lượng giác của một cung (góc) ta xác định điểm nhọn của cung (tia cuối của góc) thuộc góc phần tư nào và áp dụng bảng xét dấu các GTLG.
Xác định dấu của các biểu thức sau:
	a) A = 	b) B = 
	c) C = 	d) D = 
Cho . Xét dấu của các biểu thức sau:
	a) A = 	b) B = 
	c) C = 	d) D = 
Cho . Xét dấu của các biểu thức sau:
	a) A = 	b) B = 
	c) C = 	d) D = 
Cho tam giác ABC. Xét dấu của các biểu thức sau:
	a) A = 	b) B = 
	c) C = 	d) D = 
	a) 
VẤN ĐỀ 2: Tính các giá trị lượng giác của một góc (cung)
	Ta sử dụng các hệ thức liên quan giữa các giá trị lượng giác của một góc, để từ giá trị lượng giác đã biết suy ra các giá trị lượng giác chưa biết.
I. Cho biết một GTLG, tính các GTLG còn lại
	1. Cho biết sina, tính cosa, tana, cota
	· Từ Þ .
	– Nếu a thuộc góc phần tư I hoặc IV thì .
	– Nếu a thuộc góc phần tư II hoặc III thì .
	· Tính ;	.
	2. Cho biết cosa, tính sina, tana, cota
	· Từ Þ .
	– Nếu a thuộc góc phần tư I hoặc II thì .
	– Nếu a thuộc góc phần tư III hoặc IV thì .
	· Tính ;	.
	3. Cho biết tana, tính sina, cosa, cota
	· Tính .
	· Từ Þ .
	– Nếu a thuộc góc phần tư I hoặc IV thì .
	– Nếu a thuộc góc phần tư II hoặc III thì .
	· Tính .
	4. Cho biết cota, tính sina, cosa, tana
	· Tính .
	· Từ Þ .
	– Nếu a thuộc góc phần tư I hoặc II thì .
	– Nếu a thuộc góc phần tư III hoặc IV thì .
II. Cho biết một giá trị lượng giác, tính giá trị của một biểu thức
	· Cách 1: Từ GTLG đã biết, tính các GTLG có trong biểu thức, rồi thay vào biểu thức.
	· Cách 2: Biến đổi biểu thức cần tính theo GTLG đã biết
III. Tính giá trị một biểu thức lượng giác khi biết tổng – hiệu các GTLG
	Ta thường sử dụng các hằng đẳng thức để biến đổi:
IV. Tính giá trị của biểu thức bằng cách giải phương trình
	· Đặt Þ . Thế vào giả thiết, tìm được t. 
	 Biểu diễn biểu thức cần tính theo t và thay giá trị của t vào để tính.
	· Thiết lập phương trình bậc hai: với . Từ đó tìm x, y.
Cho biết một GTLG, tính các GTLG còn lại, với:
	a) 	b) 
	c) 	d) 
	e) 	f) 
	g) 	h) 
Cho biết một GTLG, tính giá trị của biểu thức, với:
	a) 	ĐS: 
	b) 	ĐS: 
	c) 	ĐS: 
	d) 	ĐS: 
	e) 	ĐS: 
	g) 	ĐS: 
	h) 	ĐS: 
Cho . Tính giá trị các biểu thức sau:
	a) 	b) 	c) 
	ĐS: a) 	b) 	c) 
Cho . Tính giá trị các biểu thức sau:
	a) 	b) 	c) 
	ĐS: a) 11	b) 	c) 
	a) Cho . Tính .	ĐS: 
	b) Cho . Tính .	ĐS: B = 1
	c) Cho . Tính .	ĐS: 
	a) Cho . Tính .
	b) Cho . Tính .
	ĐS: a) 	b) 
	hoặc 
	a) 
VẤN ĐỀ 3: Tính giá trị lượng giác của biểu thức bằng các cung liên kết
	Sử dụng công thức các góc (cung) có liên quan đặc biệt (cung liên kết).
Tính các GTLG của các góc sau:
	a) 
	b) 
Rút gọn các biểu thức sau:
	a) 
	b) 
	c) 
	d) 
Rút gọn các biểu thức sau:
	a) 	ĐS: A = –1
	b) 	ĐS: 
	c) 	ĐS: 
	d) 	ĐS: 
	e) 	ĐS: 
	f) 	ĐS: 
	a) 
VẤN ĐỀ 4: Rút gọn biểu thức lượng giác – Chứng minh đẳng thức lượng giác
	Sử dụng các hệ thức cơ bản, công thức lượng giác để biến đổi biểu thức lượng giác. Trong khi biến đổi biểu thức, ta thường sử dụng các hằng đẳng thức.
	Chú ý: Nếu là biểu thức lượng giác đối với các góc A, B, C trong tam giác ABC thì:
	 và 
Chứng minh các đẳng thức sau:
	a) 
	b) 
	c) 
	d) 
	e) 
	f) 
	g) 
	h) 
	i) 
	k) 
Chứng minh các đẳng thức sau:
	a) 	b) 
	c) 	d) 
	e) 	f) 
	g) 	h) 
	i) 	k) 
Cho Chứng minh: .
Rút gọn các biểu thức sau:
	a) 	b) 
	c) 	d) 
	e) 	f) 
	g) 	h) 
	i) 	k) 
Chứng minh các biểu thức sau độc lập đối với x:
	a) 	ĐS: 1
	b) 	ĐS: 1
	c) 	ĐS: –2
	d) 	ĐS: 2
	e) 	ĐS: 
	f) 	ĐS: 2
	g) 	ĐS: 
Cho tam giác ABC. Chứng minh:
	a) 	b) 
	c) 	d) 
	e) 	f) 
	g) 	h) 
	a) 
VẤN ĐỀ 5: Công thức cộng
	Hệ quả: 
Tính các giá trị lượng giác của các góc sau:
	a) 	b) 
Tính giá trị của biểu thức lượng giác, khi biết:
	a) 	ĐS: 
	b) 	ĐS: 
	c) 	ĐS: 
	d) khi và a, b là các góc nhọn.
	ĐS: 
	e) khi và . Từ đó suy ra a, b .	ĐS: ; 
Tính giá trị của các biểu thức lượng giác sau:
	a) A = 	ĐS: 
	b) B = 	ĐS: 
	c) C = 	ĐS: –3
	d) D = 	ĐS: –3
	e) E = 	ĐS: 
	f) F = 	ĐS: 
	g) G = 	ĐS: 
	h) H = 	ĐS: 4
	HD: ; 
Chứng minh các hệ thức sau:
	a) 
	b) 
	c) 
	d) 
	e) 
	f) 
Chứng minh các hệ thức sau, với điều kiện cho trước:
	a) 
	b) 
	c) 
	d) 
	HD: a) Chú ý: b = (a+b)–a	b) Chú ý: b = (a+b)–a; 2a+b=(a+b)+a
	c) Khai triển giả thiết	d) Chú ý: a+2b=(a+b)+a; a=(a+b)–b
Cho tam giác ABC. Chứng minh:
	a) 
	b) 
	c) 
	d) 
	e) 
	f) 
	g) 
	h) 
	i) 
	HD: a, b, c, d) Sử dụng (A + B) + C = 1800	e, f) Sử dụng 
	g) VT = VP = tanA	h) Khai triển 
	i) Khai triển . 
	Chú ý: Từ Þ 
	Þ 
Cho tam giác A, B, C. Chứng minh:
	a) 
	b) 
	c) 
	d) 
	e) 
	HD: a, b, c) Sử dụng và BĐT Cô–si
	d) Sử dụng 
	và 
	e) Khai triển và sử dụng câu c)
	a)