Ôn tập Chương II Đại số 10

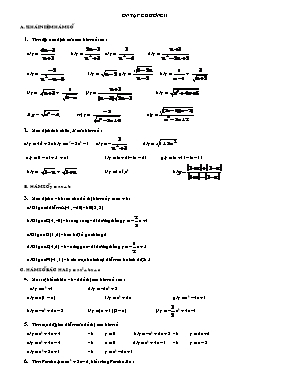
ƠN TẬP CHƯƠNG II
A. KHÁI NIỆM HÀM SỐ 
Tìm tập xác định của các hàm số sau :
a/ y = 	b/ y = 	c/ y = d/ y = 
e/ y = 	f/ y = g/ y = h/ y = + 
i/ y = + j/ y = 	k/ y = 	
l/ . m) y = 	 o)y =
Xác định tính chẵn, lẻ của hàm số :
a/ y = 4x3 + 3x	b/ y = x4 - 3x2 - 1 c/ y = -	 d/ y = 
 e/ y = |1 - x| + /1 + x|	f/ y = |x + 2| - |x - 2| g/ y = |x + 1| - |x - 1|	
h/ y = + 	i/ y = | x|5.x3	k/ 
B. HÀM SỐ y = ax + b
Xác định a và b sao cho đồ thị hàm số y = ax + b :
a/ Đi qua 2 điểm A(-1, -20) và B(3, 8)
b/ Đi qua C(4, -3) và song song với đường thẳng y = -x + 1
c/ Đi qua D(1, 2) và có hệ số góc bằng 2
d/ Đi qua E(4, 2) và vuông góc với đường thẳng y = -x + 5
e/ Đi qua M(-1, 1) và cắt trục hoành tại điểm có hoành độ là 5
C. HÀM SỐ BẬC HAI y = ax2 + bx + c
Xét sự biến thiên và vẽ đồ thị các hàm số sau :
 c/ y = x2 + 1	d/ y = -2x2 + 3
e/ y = x(1 - x)	f/ y = x2 + 2x 	g/ y = x2 - 4x + 1	
h/ y = -x2 + 2x - 3	i/ y = (x + 1)(3 - x)	j/ y = -x2 + 4x - 1
Tìm tọa độ giao điểm của đồ thị các hàm số
a/ y = x2 + 4x + 4 	và	y = 0 b/ y = -x2 + 2x + 3	và 	y = 2x + 2
c/ y = x2 + 4x - 4	và 	x = 0 d/ y = x2 + 4x - 1	và	y = x - 3
e/ y = x2 + 3x + 1	và 	y = x2 - 6x + 1
Tìm Parabol y = ax2 + 3x - 2, biết rằng Parabol đó :
a/ Qua điểm A(1; 5) b/ Cắt trục Ox tại điểm có hoành độ bằng 2
c/ Có trục đối xứng x = -3 d/ Có đỉnh I(-; -)
e/ Đạt cực tiểu tại x = 1
Tìm Parabol y = ax2 + bx + c biết rằng Parabol đó :
a/ Đi qua 3 điểm A(-1; 2) ; B(2; 0) ; C(3; 1)
b/ Có đỉnh S(2; -1) và cắt trục tung tại điểm có tung độ bằng -3.
c/ Đạt cực đại tại I(1; 3) và đi qua gốc tọa độ.
d/ Đạt cực tiểu bằng 4 tại x = -2 và đi qua B(0; 6)
e/ Cắt Ox tại 2 điểm có hoành độ là -1 và 2, cắt Oy tại điểm có tung độ bằng -2
Cho hàm số y = 2x2 + 2mx + m - 1
a/ Định m để đồ thị hàm số đi qua gốc tọa độ.	b/ Xét sự biến thiên và vẽ đồ thị (P) khi m = 1
c/ Tìm giao điểm của đồ thị (P) với đường thẳng y = -x - 1	d/ Vẽ đường thẳng này trên cùng hệ trục tọa độ của (P)
Cho (P) : y = x2 - 3x - 4 và (d) : y = -2x + m
Định m để (P) và (d) có 2 điểm chung phân biệt.
Cho (P) : y = - + 2x - 3 và (d) : x - 2y + m = 0
Định m để (P) và (d) tiếp xúc nhau. Xác định tọa độ tiếp điểm.
ƠN TẬP CHƯƠNG II
Tìm tập xác định của hàm số :
a/ y = - 	b/ y = c/ y = 
 d/ y = 	e/ y = 	f/ y = 
Xét tính chẵn, lẻ của hàm số :
a/ y = 	b/ y = c/ y = d/ y = x(x2 + 2|x|)
e/ y = 	f/ y =
Cho Parabol (P) : y = ax2 + bx + c
a/ Xác định a, b, c biết (P) qua A(0; 2) và có đỉnh S(1; 1)
b/ Khảo sát sự biến thiên và vẽ đồ thị (P) với a, b, c tìm được.
c/ Gọi (d) là đường thẳng có phương trình : y = 2x + m. Định m để (d) tiếp xúc với (P). Tìm tọa độ tiếp điểm.
Cho hàm số y = 
Định m để hàm số xác định trên toàn trục số.
Cho (P) : y = x2 - 3x - 4 và (d) : y = -2x + m. Định m để (P) và (d) :
Có 2 điểm chung phân biệt,	B. tiếp xúc 	b. không cắt nhau.