Ma trận và đề kiểm tra Toán 9 – Hình học Chương I

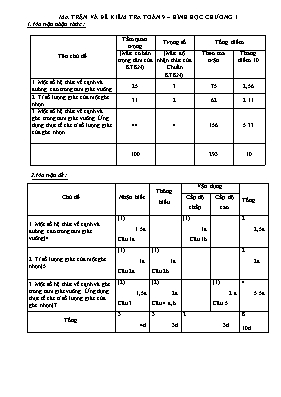
 MA TRẬN VÀ ĐỀ KIỂM TRA TOÁN 9 – HÌNH HỌC CHƯƠNG I
1. Ma trận nhận thức :
Tên chủ đề
Tầm quan trọng
Trọng số
Tổng điểm
(Mức cơ bản trọng tâm của KTKN)
(Mức độ nhận thức của Chuẩn KTKN)
Theo ma trận
Thang điểm 10
1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
25
3
75
2,56
2. Tỉ số lượng giác của một góc nhọn
31
2
62
2.11
3. Một số hệ thức về cạnh và góc trong tam giác vuông. Ứng dụng thục tế các tỉ số lượng giác của góc nhọn
44
4
156
5.33
100
293
10
 2.Ma trận đề :
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
1. Một số hệ thức về cạnh và đường cao trong tam giác vuông(4
(1)
 1.5đ 
Câu 1a
(1)
 1đ
Câu 1b 
2
 2,5đ
2. Tỉ số lượng giác của một góc nhọn(5
(1)
 1đ
Câu 2a 
(1)
 1đ Câu 2b 
2
 2đ
3. Một số hệ thức về cạnh và góc trong tam giác vuông. Ứng dụng thục tế các tỉ số lượng giác của góc nhọn(7
(2)
 1,5đ
Câu 3
(2) 
 2đ
Câu 4 a,b 
(1)
2 đ
Câu 5 
4
5.5đ
Tổng
3 
4đ
3 
3đ
2
 3đ
8
 10đ 
ĐỀ BÀI :
Câu 1: (2,5đ): Cho hình vẽ, với tam giác ABC vuông tại A, AH là đường cao 
Tính AB, AH, AC 
Từ H kẻ HE AB, HF AC, tính diện tích tam giác EHF
Câu 2: (2đ) Cho tam giác ABC vuông tại A có AB = 6cm, BC = 10cm.
Tính tất cả các tỉ số lượng giác góc B
A
B
C
H
400 
350 
Biết sin2B + cos2B = 1 .Hãy tính 
Câu 3:(1.5đ)Cho hình vẽ bên biết AB = 12cm .Hãy tính cạnh AH; AC 
Câu 4:(2đ) Hãy giải tam giác vuông ABC ?
a. ABC vuông tại A có = 480 ; BC = 10cm.
b. ABC vuông tại A có AC = 12cm, AB = 16cm.
Câu 5: ( 2đ) Một chiếc máy bay bay lên với vận tốc 520 km/h. Đường bay lên tạo với phương nằm ngang một góc 320. Hỏi sau 1,5 phút máy bay lên cao được bao nhiêu kilômét theo phương thẳng đứng? Vẽ hình minh họa
 Lưu ý :Kết quả lấy phần nguyên và 4 chữ số thập phân(nếu có); tính các góc lấy đến phút
--------------Hết-------------
HƯỚNG DẪN CHẤM VÀ ĐÁP ÁN HÌNH HỌC 9 CHƯƠNG I 
Câu 1: (2.5đ)
a.Tính các cạnh AH,AB và AC ?
Tam giác ABC vuông tại A, AH là đường cao nên
 BA2 = BH.BC = 2.8 = 16 => AB = 4 0.5đ 
 AH2 = BH.HC =2.6 = 12 => AH = 2 0.5đ 
 AC2 = HA2 + HC2 = (2 )2 + 62 => AC = 4 0.5đ 
b.Chứng minh EHFA là hình chữ nhật => tam giác EHF vuông tại H 0.25đ 
Tính HE = AH.BH:AB = 2.2:4 = 0.25đ 
 HF = AH.HC:AC = 2.6:4 = 3 0.25đ 
 Vậy S = = = 2,5980 (Đvdt) 0.25đ 
Câu 2: (2đ) Cho tam giác ABC vuông tại A có AB = 6cm, BC = 10cm.
a .Tính tất cả các tỉ số lượng giác góc B
Áp dụng Định lý Pitago tính AC = 8cm 	0.25đ
sinB = 8/10 = 4/5 ;cosB = 6/10 = 3/5 ,tanB = 8/6 = 4/3; cotB = 6/8 = 3/4 0.75đ
b. 
= (cos2200 + cos2700 ) + (cos2400 + cos2500 ) = (sin2700 + cos2700 ) + ( sin2500 + cos2500 )
= 1 + 1 = 2 1đ
Câu 3: (1.5đ) Cho hình vẽ bên biết AB = 12cm .Hãy tính cạnh AH; AC
Tam giác ABH vuông tại H nên AH = AB.sinB = 12.sin400 = 7,7134 cm 0.75đ
Tam giác ABH vuông tại H nên AC = AH/sinC = 7,7134/sin350 = 13,4479 cm 0.75đ
Câu 4: (2đ) Hãy giải tam giác vuông ABC ?
a. ABC vuông tại A có = 480 ; BC = 10cm.
Tính góc B = 420 0.25 đ
Tính cạnh AB = CB.sinC = 10.sin400 = 7,4314 cm 
 AC = 6,6913 cm ( tính đúng các cạnh cho 0.75đ ; đúng 1 cạnh 0.5đ )
b. ABC vuông tại A có AC = 12 cm, AB = 16 cm.
Tính cạnh BC = 20cm 0.5 đ 
 SinC = 16/20 => C = 5307’ 0.25 đ ; SinB = 12/20 => B = 36052’ 0.25 đ
Câu 5: (2đ)
- Gọi AB là đoạn đường máy bay bay lên trong 1,5 phút. 
B
C
A
320
- Cạnh BC là độ cao máy bay đạt được sau 1,5 phút đó 0.25đ
Vì 1,5 phút = giờ nên Vẽ hình 0.25đ
 AB = = 13 (km) 0.5đ
Do đó: BC 	= AB.sinA = 13.sin320
	= 6,8889 (km) 0.75đ
Vậy sau 1,5 phút máy bay lên cao được 6,8889 km 0.25đ
--------------Hết-------------