Kiến thức cơ bản Hình học 9

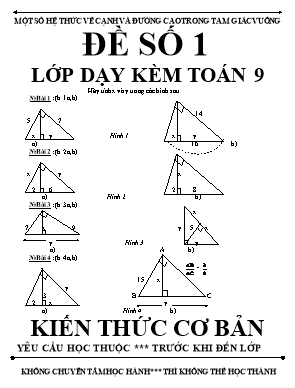
 MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
 ĐỀ SỐ 1
 LỚP DẠY KÈM TOÁN 9
 Hãy tính x và y trong các hình sau
№Bài 1 : (h.1a,b)
	 14
 5 7
 x y Hình 1	x y
 a) 16 b)
№Bài 2 : (h.2a,b)
 x y	 x
 2 6	2 8	
	a) Hình 2	b)	
№Bài 3 : (h.3a,b)
	 x
 7 x 9 	 y 5	 x
 y Hình 3	 y
	a) A	b) 	 	 
№Bài 4 : (h.4a,b)
	 = 
	 15	 x 
 y	 
 3	 	 B C
 2 x	y	
	a) Hình 4 b)
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
	 BÀI 1 * MỘT SỐ HỆ THỨC VỀ CẠNH VÀ
 ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
	1- HỆ THỨC GIỮA CẠNH GÓC VUÔNG VÀ HÌNH CHIẾU CỦA NÓ TRÊN CẠNH HUYỀN 
 Định lí 1
 Trong một tam giác vuông, bình phương một cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
 Như vậy,trong tam giác ABC vuông tại A ta nhận được	
 AB2 = BC.BH c2 = a.c’ 
 AC2 = BC.CH b2 = a.b’ 	 	 	 
 2- MỘT SỐ HỆ THỨC LIÊN QUAN TỚI ĐƯỜNG CAO
Định lí 2
 Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Như vậy, Trong ΔABC vuông tại A (hình định lí 1), ta nhận được:	
	 AH2 = BH.HC h2 = c’.b’
Định lí 3
 Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
Như vậy, Trong ΔABC vuông tại A (hình định lí 1), ta nhận được:
	 AB.AC = AH.BC b . c = a . h.
Định lí 4
 Trong một tam giác vuông, nghịch đảo bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Như vậy, Trong ΔABC vuông tại A (hình định lí 1), ta nhận được:
	 = + = + .
 TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
 ĐỀ SỐ 2
 LỚP DẠY KÈM TOÁN 9
 №Bài 1 : Vẽ một tam giác vuông có một góc nhọn bằng 400 rồi viết các tỉ số lượng giác của góc 400.
№Bài 2 : Cho tam giác ABC vuông tại A. Chứng minh rằng = .	
№Bài 3 : Cho tam giác ABC vuông tại A. = 300 C
BC = 8cm. Hãy tính cạnh AB(làm tròn đến chữ
số thập phân thứ ba), biết rằng cos 300 0,866.
№Bài 4 : Cho tam giác ABC vuông tại A. AB = 6cm	 α
= α (h.9)	 A 6cm B
Biết tg α = , hãy tính : Hình 9	
a) Cạnh AC; 	 b) Cạnh BC. 
№Bài 5 : Tìm giá trị x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình 10, biết rằng:
	tg 470 1,072; cos 380 0,788.
	 16
	 380
 x 63 	 x
 470
	a)	Hình 10	 b)
№Bài 6 : Cho tam giác ABC vuông tại A, trong đó AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra tỉ số lượng giác của góc C.
№Bài 7 : Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư), biết rằng :
AB = 13; BH = 5. 	b)BH = 3; CH = 4.
№Bài 8 : Hãy biến đổi các tỉ số lượng giác sau đây thành tỉ số lượng giác của các góc nhỏ hơn 450 : sin750, cos530, sin47020’, tg620, cotg82045’.
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
	 BÀI 2 * TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
 1* KHÁI NIỆM VỀ TỈ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
	a) Mở đầu
	Cho tam giác ABC vuông tại A. Xét góc nhọn B của nó.	A
Cạnh AB được gọi là cạnh kề của góc B.
Cạnh AC được gọi là cạnh đối của góc B.
Ta đã biết : Hai tam giác vuông đồng dạng với nhau khi
và chỉ khi chúng có cùng số đo của một góc nhọn, hoặc tỉ số	B C 
 các tỉ số giữa cạnh đối và cạnh kề của một góc nhọn trong một tam giác đó như nhau. Như vậy, tỉ số giữa cạnh đối và cạnh kề của một góc nhọn trong một tam giác vuông đặt trưng cho độ lớn của góc nhọn đó.
 b) Định nghĩa : Cho góc nhọn α . Vẽ một tam giác vuông có góc nhọn α .
Cách vẽ : Vẽ góc α, từ một điểm bất kì trên một cạnh của góc α kẻ đường vuông góc với cạnh kia , xác định cạnh đối và cạnh kề của góc α. Khi đó:
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α.Kí hiệu: sin α
Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α. Kí hiệu: cos α
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α.Kí hiệu: tg α (hay tan α)
Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α.
Kí hiệu: cotg α(hay cot α)
sin α = ; cos α = ;
tg α = ; cotg α = ;
	Nhận xét : Từ định nghĩa trên ta nhận thấy tỉ số lượng giác của một góc nhọn luôn luôn 
dương. Hơn nữa sin α < 1 , cos α < 1. 
 TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
 ĐỀ SỐ 3
 LỚP DẠY KÈM TOÁN 9
№Bài 1 : Cạnh góc vuông kề với góc 600 của một tam giác vuông bằng 3. Sử dụng bảng lượng giác của các góc đặt biệt, hãy tìm cạnh huyền và cạnh góc vuông còn lại (làm tròn đến chữ số thập phân thứ tư).
№Bài 2 :Đường cao BD của tam giác nhọn ABC bằng 6;đoạn thẳng AD bằng 5
a) Tính diện tích tam giác ABD ; 
b) Tính AC, dùng các thông tin dưới đây nếu cần : sinC = , cosC = , tgC = .
№Bài 3 : Cho cosα = 0,8 . Hãy tìm sinα, tgα, cotgα (làm tròn đến chữ số thập phân thứ tư).
№Bài 4 : Hãy tìm sinα, cosα (làm tròn đến chữ số thập phân thứ tư) nếu biết
a) tgα = ; b) cotgα = .	
№Bài 5 : Dựng góc nhọn α, biết rằng 	
a) sinα = 0,25; 	 b) cosα = 0,75 ; 8	
c) tgα = 1 ;	 	 d) cotgα = 2.
№Bài 6 : Cho hình 12. 	 
Hãy viết một phương trình để từ đó 700
có thể tìm được x(không phải giải phương trình này).	x 4
№Bài 7 : Cho hình 13.
Hãy tính sinL. (làm tròn đến chữ số 300 800	
thập phân thứ tư), biết rằng sin300 = 0,5	L	Hình 12
	 4,2
	 300 
	N 2,8 M	 
	Hình 13.
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
	 BÀI 2 * TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
2* TỈ SỐ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU. A
VÍ DỤ 4: (?4/tr 74 – SGK). Cho hình 19. 
Hãy cho biết tổng số đo của hai góc
	của góc α và góc β. Lập các tỉ số lượng giác của góc α. B α β C
và góc β. Trong các tỉ số này, hãy cho biết các cặp tỉ số bằng nhau. Hình 19.
	 Bài giải :
 Ta có : α + β = 900. Theo định nghĩa các tỉ số lượng giác của một góc nhọn với h.19
	Ta có : sin α = ; cos α = ; tg α = ; cotg α = ; 
sin β = ; cos β = ; tg β = ; cotg β = ;
Từ đó rút ra : sin α = cos β ( = );	cos α = sin β ( = )
Định lí :	 tg α = 	cotg β (= ); cotg α = tg β (= ).
 Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
 BẢNG TỈ SỐ LƯỢNG GIÁC CỦA CÁC GÓC ĐẶC BIỆT
	 α
 Tỉ số lượng giác
 300
 450
 600
 sin α
 cos α
 tg α
 1
 cotg α
 1
 MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
 ĐỀ SỐ 4
 LỚP DẠY KÈM TOÁN 9
№Bài 1: Các cạnh của một tam giác có độ dài 4cm, 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó.
№Bài 2 : Tam giác ABC vuông tại A có AB = 21cm,= 400. Hãy tính các độ dài
a) AC;	b) BC;	c) Phân giác BD.
№Bài 3 : Cho hình 16. Biết :	A
AB = AC = 8cm, CD = 6cm, = 340 340420
và = 420. Hãy tính :	 8 8
a) Độ dài cạnh BC;	D
b) ;	 6
c) Khoảng cách từ điểm B đến cạnh AD.	B
	 C Hình 16.	
№Bài 4: Cho tam giác ABC trong đó AB = 5cm, AC = 8cm, = 200. Tính diện tích tam giác ABC, có thể dùng các thông tin dưới đây nếu cần
sin2000,3420, cos2000,9397, tg2000,3640.
№Bài 5 : Từ đỉnh một ngọn đèn biển
cao 38m so với mặt nước biển, người 	300
ta nhìn thấy một hòn đảo dưới góc	38m
300 so với đường nằm ngang chân đèn Hình 17.
(h.17). Hỏi khoảng cách từ đảo đến
chân đèn (ở mực nước biển) bằng bao nhiêu ?	
№Bài 6: Trong tam giác ABC 	A
có AB = 11cm, = 380, = 300.	 11
N là chân đường vuông góc kẻ từ A
đến BC (h.18). Hãy tính AN, AC 300 380
 C N B
	Hình 18
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
 BÀI 4 * MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
 	 A
	 1* CÁC HỆ THỨC 	 
Cho tam giác ABC vuông tại A, cạnh huyền a và 
 cạnh góc vuông b, c (h.25) c b
 B a C 
 VÍ DỤ 1: (?1/tr 85 – SGK). Viết các tỉ số lượng giác của góc B và góc C. Từ đó hãy tính mỗi cạnh góc vuông theo:
Cạnh huyền và các tỉ số lượng giác của góc B và góc C.
Cạnh góc vuông còn lại và các tỉ số lượng giác của góc B và góc C.
 	Bài giải :
Ta có :
sin B = = b = a sin B; cos B = = c = a cos B.
sin C = = c = a sin C; cos C = = b = a cos C
 b) Ta có :
tg B = = b = c tg B ; cotg B = = c = b cotg B.
tg C = = c = b tg C ; cotg C = = b = c cotg C.
	Từ kết quả trên ta có định lí :
 	Định lí : Trong tam giác vuông, mỗi cạnh góc vuông bằng :
Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề ;
Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
 Như vậy, trong tam giác ABC vuông tại A, ta có các hệ thức :
	b = a .sin B = a .cos C ;	b = c .tg B = c . cotg C.
	c = a .sin C = a .cos B ;	c = b .tg C = b . cotg B.
 MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
 ĐỀ SỐ 5
 LỚP DẠY KÈM TOÁN 9
№Bài 1 : Tìm x và y trong các hình sau (h.20):
	C 	 D 4 C
	 C	 500
	 500	4
 8 	y	x 7	 x
	x	 700
 300	 600 400
 A P B A 	A P y Q B
	y	D B	AB//CD
	a)	b)	 c) Q	
№Bài 2 : Cho hình 21. Biết:
 = 180,
 = 1500,	 8
QT = 8cm,
TR = 5cm,
Hãy tính	 180 1500
PT; P	 T 5 R
Diện tích tam giác PQR. 	 Hình 21.
№Bài 3 : (h.22)	D
Cho BCD là tam giác đều
cạnh 5cm và góc DAB bằng
400. Hãy tính
a) AD;
b) AB.
	400
 	 A B Hình 22 C
№Bài 4 : Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm,
HC = 64cm, tính , .
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
 BÀI 4 * MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
 2. ÁP DỤNG GIẢI TAM GIÁC VUÔNG:
	Trong một tam giác vuông, nếu cho biết trước hai cạnh hoặc một cạnh và một góc nhọn thì ta sẽ tìm được tất cả các cạnh và góc còn lại của nó. Bài toán đặt ra như thế gọi là bài toán
 “ Giải tam giác vuông”.
	Ví dụ 3 : Cho tam giác vuông ABC với các cạnh góc vuông AB = 5 
 AC = 8 (h.27). Hãy giải tam giác vuông ABC. C
 	Bài giải :
	Theo định lí py-ta-go, ta có:
	BC = = 9,434 8
	Mặt khác 
	tg C = = = 0,625	 
	Tra bảng hay sử dụng máy tính bỏ túi, ta tìm được A 5 B
	 320, do đó 900 – 320 580.	 Hình 27.
VÍ DỤ 2: (?2/tr 87 – SGK). Trong ví dụ 3, hãy tính cạnh BC mà không áp dụng định lí py-ta-go.
 	Bài giải :
	Ta có: tg B = = 1,6 580.	P
	BC = = 9,434.	 360
	Ví dụ 4 : Cho tam giác OPQ vuông tại O có = 360, 7
PQ = 7 (h.28). Hãy giải tam giác vuông OPQ.
 	Bài giải :
	Ta có = 900 – = 900 – 360 = 540 	 O Q
	Theo các hệ thức giữa cạnh và góc trong tam giác vuông Hình 28
 ta có :
	OP = PQ.sin Q = 7.sin 540 5,663.
	OQ = PQ.sin P = 7.sin 360 4,114.
 SỰ XÁC ĐỊNH CỦA ĐƯỜNG TRÒN
 TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN
 ĐỀ SỐ 6
 LỚP DẠY KÈM TOÁN 9
№Bài 1 : Cho hình chữ nhật ABCD có AD = 12cm, CD = 16cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
№Bài 2 : Cho góc nhọn xOy và hai điểm D, E thuộc tia Oy. Dựng đường tròn tâm M đi qua D và E sao cho tâm M đi qua tia Ox.
№Bài 3: Cho hình vuông ABCD, O là giao điểm của hai đường chéo, 
OA = cm. Vẽ đường tròn tâm A bán kính 2cm. Trong năm điểm A, B, C, D, O,
điểm nào nằm trên đường tròn ? Điểm nào nằm trong đường tròn ? Điểm nào nằm ngoài đường tròn ?
№Bài 4 : Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC, nó cắt các cạnh AB, AC theo thứ tự ở D, E.
Chứng minh rằng CDAB, BEAC.
Gọi K là giao điểm của BE và CD. Chứng minh rằng AK vuông góc với BC.
№Bài 5 : Cho hình vuông ABCD.
Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó.
Tính bán kính của đường tròn đó, biết cạnh của hình vuông bằng 2dm.
№Bài 6 : Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường tròn ở D. 
Vì sao AD là đường kính đường tròn (O) ?
Tính số đo góc ACD.
Cho BC = 24cm, AC = 20cm. Tính đường cao AH và bán kính đường tròn (O).
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
 BÀI 1 *SỰ XÁC ĐỊNH CỦA ĐƯỜNG TRÒN TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN.
 O . R
1* NHẮC LẠI VỀ ĐƯỜNG TRÒN
 Định nghĩa: Đường tròn tâm O, bán kính R (với R > 0)
 là hình gồm các điểm cách O một khoảng bằng R.
 Đường tròn như vậy được kí hiệu : (O; R) trong trường hợp 
không cần chú ý đến bán kính có thể sử dụng kí hiệu (O) . 
	* Vị trí tương đối của điểm và đường tròn :	
Cho đường tròn (O; R) và điểm M, ta có :
Nếu OM < R M nằm trong đường tròn.
Nếu OM = R M nằm trên đường tròn.
Nếu OM > R M nằm ngoài đường tròn.
Nhận xét : “ Nếu = 900 thì M thuộc đường tròn đường kính AB”
2* CÁCH XÁC ĐỊNH ĐƯỜNG TRÒN
Nhận xét : 
1.Một điểm O cho trước và một số thực R > 0 cho trước xác định một đường tròn (O; R).
2. Một đoạn thẳng AB cho trước xác định một đường tròn đường kính AB.
3. Ba điểm không thẳng hàng A, B, C xác định một và chỉ một đường tròn đi qua ba điểm đó ( gọi là đường tròn ngoại tiếp ΔABC ). 
3* TÂM ĐỐI XỨNG 
 Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
4* TRỤC ĐỐI XỨNG 
 Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
 ĐƯỜNG KÍNH VÀ DÂY CỦA ĐƯỜNG TRÒN
 ĐỀ SỐ 7
 LỚP DẠY KÈM TOÁN 9
№Bài 1 : Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng :
Bốn điểm B, C, H, K cùng thuộc một đường tròn;
HK < BC.
№Bài 2 : Tứ giác ABCD có = = 900.
Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn.
So sánh độ dài AC và BD. Nếu AC = BD thì tứ giác ABCD là hình gì ?
№Bài 3 : Cho nửa đường tròn tâm O, đường kính AB và dây EF không cắt đường kính. Gọi I và K lần lượt là chân các đường vuông góc kẻ từ A và B đến EF. 
Chứng minh rằng IE = KF.
№Bài 4 : Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
№Bài 5 : Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tâm D bán kính R, cung này cắt đường tròn (O) ở B và C.
Tứ giác OBDC là hình gì ? Vì sao ?
Tính số đo các góc CBD, CBO, OBA.
Chứng minh rằng tam giác ABC là tam giác đều.
№Bài 6 : Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. Hãy cho biết ACBD là hình gì ? Vì sao ?
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
 BÀI 2 * ĐƯỜNG KÍNH VÀ DÂY CỦA ĐƯỜNG TRÒN
1* SO SÁNH ĐỘ DÀI CỦA ĐƯỜNG KÍNH VÀ DÂY
 Trong các dây của đường tròn, dây lớn nhất là đường kính 
Định lí 1: 
2- QUAN HỆ VUÔNG GÓC GIỮA ĐƯỜNG KÍNH VÀ DÂY:
Định lí 2 :
 Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
 Định lí 3 :	
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
	 AB là đường kính
	 AB cắt CD tại I AB CD
	I O ; CI = ID 
	VÍ DỤ 2: (?1/tr 104 – SGK). Cho hình 67. Hãy tính độ dài dây AB, biết
 O 
 M
	OA = 13cm, AM = MB, OM = 5cm.
 Bài giải :
 OM đi qua trung điểm M của dây AB (AB không đi qua O)
 	 nên OM AB 
	Theo định lí py-ta-go, ta có :	 
	AM2 = OA2 – OM2	 A B
	 = 132 – 52 = 144
	 AM = = 12 (cm) 
 AB = 2.AM = 2.12 = 24 (cm).
 LIÊN HỆ GIỮA DÂY VÀ KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY
 ĐỀ SỐ 8
 LỚP DẠY KÈM TOÁN 9
№Bài 1 : Cho hình vẽ, trong đó hai dây CD, EF bằng nhau và vuông góc với nhau tại I, 
IC = 2cm, ID = 14cm.
Tính khoảng cách từ O đến mỗi dây.
	 E
	 O	 
	 I	 
	C D
 F
№Bài 2 : Cho đường tròn (O), dây AB và dây CD AB < CD. Giao điểm K của các đường 
thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O; OK) cắt KA và KC tại M và N
Chứng minh rằng KM < KN.
№Bài 3 : Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Chứng minh rằng dây AB vuông góc với OI tại I ngắn hơn mọi dây khác đi qua I.
№Bài 4 : Tam giác ABC nội tiếp đường tròn (O) có Â > > . Gọi OH, OI, OK theo thứ tự là khoảng cách từ O đến BC, AC, AB. So sánh các độ dài OH, OI, OK.
№Bài 5: Cho đường tròn (O), hai dây AB và CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết
 AB > CD, chứng minh rằng MH > MK.
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
 BÀI 3 * LIÊN HỆ GIỮA DÂY VÀ KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY
1* BÀI TOÁN : Cho AB và CD là hai dây (khác đường kính )của đường tròn
 (O ;R). Gọi OH, OK theo thứ tự là các khoảng cách từ O đến AB, CD. 
Chứng minh rằng OH2 + HB2 = OK2 + KD2
 	 Bài giải :
 K
 O R
 H 
	 C Áp dụng định lí py-ta-go vào các tam giác vuông 
 OHB và OKD
	 	ta có : OH2 + HB2 = OB2 = R2 (1)
	 	 OK2 + KD2 = OD2 = R2 (2)
 D Từ (1) và (2) suy ra 
	 	OH2 + HB2 = OK2 + KD2
 A B * Trường hợp có một dây là đường kính 
 chẳng hạn là AB thì H trùng với O
ta có OH = 0 và HB2 = R2 = OK2 + KD2
 * Trường hợp cả hai dây AB và CD đều là đường kính thì H và K đều trùng với O , ta có OH = OK = 0 và HB2 = R2 = KD2
	 2- LIÊN HỆ GIỮA DÂY VÀ KHOẢNG CÁCH TỪ TÂM ĐẾN DÂY 
Định lí 1 
 Trong một đường tròn :
Hai dây bằng nhau thì cách đều tâm.
Hai dây cách đều tâm thì bằng nhau.
Định lí 2 
 Trong hai dây của một đường tròn :
Dây nào lớn hơn thì dây đó gần tâm hơn.
Dây nào gần tâm hơn thì dây đó lớn hơn.
 VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
 ĐỀ SỐ 9
 LỚP DẠY KÈM TOÁN 9
№Bài 1 : Trên mặt phẳng tọa độ cho điểm I có tọa độ (– 3 ; 2). Nếu vẽ đường tròn tâm I bán kính bằng 2 thì đường tròn đó có vị trí như thế nào đối với các trục tọa độ ?
№Bài 2 : Cho đường thẳng a. Tâm I của tất cả các đường tròn có bán kính 5cm và tiếp xúc với đường thẳng a nằm trên đường nào ?
№Bài 3 : Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A; 13cm)
Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy.
Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
№Bài 4 : Cho đường tròn (O) bán kính 2cm. Một đường thẳng đi qua điểm A nằm bên ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB = BC. Kẻ đường kính 
COD. Tính độ dài AD.
№Bài 5 :Cho đường tròn (O; 2cm), điểm A di chuyển trên đường tròn. Trên tiếp tuyến tại A, lấy điểm M sao cho AM = OA. Điểm M chuyển động trên đường nào ?
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
 BÀI 4 * VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
1* BA VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
	 a) Đường thẳng và đường tròn cắt nhau :
 R
 H O
 Khi đường thẳng a và đường tròn (O) có hai điểm chung A và B
 B	a (O) = a và (O) cắt nhau.
	Ta nói đường thẳng a và đường tròn (O) cắt nhau. Đường thẳng a còn được gọi là cát tuyến của đường tròn (O) .
	Khi đó OH < R và HA = HB = 
 A 
 a b) Đường thẳng và đường tròn tiếp xúc nhau:
 O
	Khi đường thẳng a và đường tròn (O) chỉ có một điểm chung C, ta nói đường thẳng a và đường tròn (O) tiếp xúc nhau
 Ta còn nói đường thẳng a là tiếp tuyến của đường tròn (O) 
	điểm C gọi là tiếp điểm.
	 a (O) = a tiếp xúc với (O).
	Khi đó H C, OC a và OH = R. 
 Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
 Định lí
 a C H
c) Đường thẳng và đường tròn không giao nhau	
 O
 Khi đường thẳng a và đường tròn (O) không có điểm chung
 ta nói đường thẳng a và đường tròn (O) không giao nhau.
	 a (O) = a và (O) không giao nhau.
	khi đó OH > R
a H
 DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
 ĐỀ SỐ 10
 LỚP DẠY KÈM TOÁN 9
№Bài 1 : Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Dùng thước và compa, hãy dựng các điểm B và C thuộc đường tròn (O) sao cho AB và AC là các tiếp tuyến của đường tròn (O).
№Bài 2 : Cho điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Dựng đường tròn (O) đi qua A và B, nhận đường thẳng d làm tiếp tuyến.
№Bài 3 : Cho tam giác ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường tròn (O) có đường kính AH. Chứng minh rằng :
a) Điểm E nằm trên đường tròn (O);
b) DE là tiếp tuyến của đường tròn (O).
№Bài 4 : Cho góc nhọn xOy, điểm A thuộc tia Ox.
Dựng đường tròn tâm I tiếp xúc với Ox tại A và có tâm I nằm trên tia Oy.
№Bài 5 : Cho đường tròn (O) và đường thẳng d không giao nhau. Dựng tiếp tuyến của đường tròn (O) sao cho tiếp tuyến đó song song với d.
№Bài 6 : Xét tính đúng – sai của mỗi khẳng định sau :
a) Nếu đường thẳng d tiếp xúc với đường tròn (O) tại A thì d vuông góc với OA.
b) Nếu đường thẳng d vuông góc với bán kính OA của đường tròn (O) thì d là tiếp tuyến của đường tròn.
 KIẾN THỨC CƠ BẢN
 YÊU CẦU HỌC THUỘC *** TRƯỚC KHI ĐẾN LỚP 
 BÀI 5 * DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
1*DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
Ta đã có các kết quả sau:
Nếu một đường thẳng và một đường tròn chỉ có một điểm chung thì đường thẳng đó là
 tiếp tuyến của đường tròn.
Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường
 tròn