Kiểm tra một tiết - Năm học 2012 – 2013 môn: Toán Đại số – lớp: 10 cơ bản

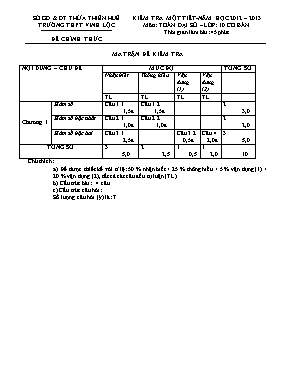
SỞ GD & ĐT THỪA THIÊN HUẾ
TRƯỜNG THPT VINH LỘC
ĐỀ CHÍNH THỨC
KIỂM TRA MỘT TIẾT-NĂM HỌC 2012 – 2013
Môn: TOÁN ĐẠI SỐ – LỚP: 10 CƠ BẢN
Thời gian làm bài: 45 phút
MA TRẬN ĐỀ KIỂM TRA
NỘI DUNG – CHỦ ĐỀ
MỨC ĐỘ
TỔNG SỐ
Nhận biết
Thông hiểu
Vận dụng (1)
Vận dụng (2)
TL
TL
TL
TL
Chương I
Hàm số
Câu 1.1 
 1,5đ
Câu 1.2 
 1,5đ
2
 3,0
Hàm số bậc nhất
Câu 2.1
 1,0đ
Câu 2.2
 1,0đ
2
 2,0
Hàm số bậc hai
Câu 3.1
 2,5đ
Câu 3.2
 0,5đ
Câu 4.
 2,0đ
3 
 5,0
TỔNG SỐ
3	 
 5,0
2
 2,5
1
 0,5
1
 2,0
 10
Chú thích: 
a) Đề được thiết kế với tỉ lệ: 50 % nhận biết + 25 % thông hiểu + 5 % vận dụng (1) + 20 % vận dụng (2), tất cả các câu đều tự luận (TL).
b) Cấu trúc bài: 4 câu
c) Cấu trúc câu hỏi:
Số lượng câu hỏi (ý) là: 7.
SỞ GD & ĐT THỪA THIÊN HUẾ KIỂM TRA MỘT TIẾT-NĂM HỌC 2012 - 2013
 TRƯỜNG THPT VINH LỘC	 Môn: TOÁN ĐẠI SỐ – LỚP: 10 CƠ BẢN
 Thời gian làm bài: 45 phút
 ĐỀ CHÍNH THỨC ĐỀ SỐ 1
Câu 1: (3,0 điểm) Tìm tập xác định của các hàm số sau:
1/. 2/. 
Câu 2: ( 2,0 điểm) 
	1/. Xét tính chẵn, lẻ của hàm số sau: 
	2/. Vẽ đồ thị hàm số: 
Câu 3: (3,0 điểm) 
1/. Lập bảng biến thiên và vẽ đồ thị (P) của hàm số: 
2/. Tìm tọa độ giao điểm của (P) và đường thẳng 
Câu 4: (2,0 điểm) Xác định Parabol (P): biết (P) nhận đường thẳng làm trục đối xứng, đi qua và cắt trục tung tại điểm có tung độ bằng 
HẾT
SỞ GD & ĐT THỪA THIÊN HUẾ KIỂM TRA MỘT TIẾT-NĂM HỌC 2012 - 2013
 TRƯỜNG THPT VINH LỘC	 Môn: TOÁN ĐẠI SỐ – LỚP: 10 CƠ BẢN
 Thời gian làm bài: 45 phút (Chương II)
 ĐỀ CHÍNH THỨC	ĐỀ SỐ 2
Câu 1: (3,0 điểm) Tìm tập xác định của các hàm số sau:
1/. 2/. 
Câu 2: ( 2,0 điểm) 
	1/. Xét tính chẵn, lẻ của hàm số sau: 
	2/. Vẽ đồ thị hàm số: 
Câu 3: (3,0 điểm) 
1/. Lập bảng biến thiên và vẽ đồ thị (P) của hàm số: 
2/. Tìm tọa độ giao điểm của (P) và đường thẳng 
Câu 4: (2,0 điểm) Xác định Parabol biết Parabol có đỉnh nằm trên trục hoành và đi qua hai điểm và 
HẾT
SỞ GD & ĐT THỪA THIÊN HUẾ KIỂM TRA MỘT TIẾT-NĂM HỌC 2012 - 2013
 TRƯỜNG THPT VINH LỘC	 Môn: TOÁN ĐẠI SỐ – LỚP: 10 CƠ BẢN
 Thời gian làm bài: 45 phút (Chương II)
 ĐỀ CHÍNH THỨC
ĐÁP ÁN VÀ THANG ĐIỂM
(Đề 1)
(Đáp án này gồm trang)
CÂU
Ý
Nội dung
Điểm
1
Tìm tập xác định của các hàm số sau:
1/. 2/. 
1.1
Tập xác định: 
1,5đ
1.2
Hàm số xác định 
0,5đ
0,5đ
Vậy tập xác định của hàm số là: 
0,5đ
2
1/. Xét tính chẵn, lẻ của hàm số sau: 
TXĐ: 
0,25đ
2.1
 và 
0,5đ
Vậy hàm số đã cho là hàm số lẻ
0,25đ
2.2
2/. Vẽ đồ thị hàm số: 
1,0đ
3
3.1
1/. Lập bảng biến thiên và vẽ đồ thị (P) của hàm số: 
BBT:
	2
-1
1,0đ
Đỉnh I(2; -1)
0,25đ
Trục đối xứng là đường thẳng: x = 2
0,25đ
Giao điểm của đồ thị và trục tung: (0; 3)
0,25đ
Giao điểm của đồ thị và trục hoành: (1; 0) và (3; 0)
0,25đ
Đồ thị: 
0,5đ
3.2
2/. Tìm tọa độ giao điểm của (P) và đường thẳng 
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:
0,25đ
Vậy có hai giao điểm có tọa độ là: (-1; 8) và (6; 15).
0,25đ
4
Xác định Parabol (P): biết (P) nhận đường thẳng làm trục đối xứng, qua và cắt trục tung tại điểm có tung độ bằng 
(P) nhận đường thẳng làm trục đối xứng nên: 
0,5đ
(P) qua nên: 
0,25đ
(P) cắt trục tung tại điểm có tung độ bằng -2 nên 
0,5đ
Từ (1), (2), (3) ta có: 
0,5đ
Vậy (P): 
0,25đ
---Hết---
SỞ GD & ĐT THỪA THIÊN HUẾ KIỂM TRA MỘT TIẾT-NĂM HỌC 2012 - 2013
 TRƯỜNG THPT VINH LỘC	 Môn: TOÁN ĐẠI SỐ – LỚP: 10 CƠ BẢN
 Thời gian làm bài: 45 phút (Chương II)
 ĐỀ CHÍNH THỨC
ĐÁP ÁN VÀ THANG ĐIỂM
(Đề 2)
(Đáp án này gồm trang)
CÂU
Ý
Nội dung
Điểm
1
Tìm tập xác định của các hàm số sau:
1/. 2/. 
1.1
Tập xác định: 
1,5đ
1.2
Hàm số xác định 
0,5đ
0,5đ
Vậy tập xác định của hàm số là: 
0,5đ
2
1/. Xét tính chẵn, lẻ của hàm số sau: 
TXĐ: 
0,25đ
2.1
 và 
0,5đ
Vậy hàm số đã cho là hàm số chẵn
0,25đ
2.2
2/. Vẽ đồ thị hàm số: 
1,0đ
3
3.1
1/. Lập bảng biến thiên và vẽ đồ thị (P) của hàm số: 
BBT:
	1
2
1,0đ
Đỉnh I(1; - 4)
0,25đ
Trục đối xứng là đường thẳng: x = 1
0,25đ
Giao điểm của đồ thị và trục tung: (0; - 3)
0,25đ
Giao điểm của đồ thị và trục hoành: (- 1; 0) và (3; 0)
0,25đ
Đồ thị: 
3.2
2/. Tìm tọa độ giao điểm của (P) và đường thẳng 
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:
0,25đ
Vậy có hai giao điểm có tọa độ là: (2; 9) và (3; 12).
0,25đ
4
Xác định Parabol biết Parabol có đỉnh nằm trên trục hoành và qua và 
Parabol có đỉnh nằm trên trục hoành nên ta có: 
0,5đ
Parabol đi qua A và B nên ta có: 
	 (2)
 và 
0,25đ
0,5đ
Từ (1), (2), (3), ta có: 
0,5đ
Vậy 
0,25đ
---Hết---