Kiểm tra môn: Giải tích 12 (tiết 18) thời gian: 45’

Ngày soạn:2/10/2012
A.mục tiêu:
Tiết 18:Kiểm tra 45 phút
Kiểm tra kiến thức :Các kiến thức đã học về tính đơn điệu của hàm số, cực đại cực tiểu, giá trị lớn nhất, nhỏ nhất của hàm số, tiệm cận.Tìm được khoảng đơn điệu , các đường tiệm cận ,GTLN, GTNN.Tự giác tích cực trong học tập.Biết phân biệt rõ các khái niệm cơ bản và vận dụng trong từng trường hợp cụ thể.Tư duy các vấn đề của toán học một cách logic và hệ thống.
B.chuẩn bị của gv và hs
GV:Chuẩn bị bài kiểm tra.
HS:Cần ôn lại một số kiến thức đã học ở bài trước.
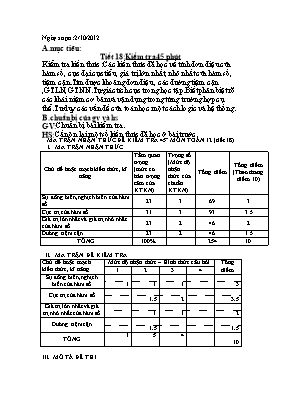
MA TRẬN NHẬN THỨC ĐỀ KIỂM TRA 45’ MÔN TOÁN 12 (tiết 18)
MA TRẬN NHẬN THỨC
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm quan trọng (mức cơ bản trọng tâm của KTKN)
Trọng số (Mức độ nhận thức của chuẩn KTKN)
Tổng điểm
Tổng điểm (Theo thang điểm 10)
Sự đồng biến, nghịch biến của hàm số
23
3
69
3
Cực trị của hàm số
31
3
93
3.5
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
23
2
46
2
Đường tiệm cận
23
2
46
1.5
TỔNG
100%
254
10
MA TRẬN ĐỀ KIỂM TRA
Chủ đề hoặc mạch kiến thức, kĩ năng
Mức độ nhận thức – Hình thức câu hỏi
Tổng điểm
1
2
3
4
Sự đồng biến, nghịch biến của hàm số
1
1
1
3
Cực trị của hàm số
1.5
2
3.5
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
1
2
Đường tiệm cận
1.5
1.5
TỔNG
1
5
4
10
III. MÔ TẢ ĐỀ THI
Câu
Nội dung
Mức độ
Điểm
1
Sự đồng biến, nghịch biến của hàm số
3
a) Xét sự đồng biến, nghịch biến của hàm số
Thông hiểu
b) CMR hàm số đồng biến (nghịch biến) trên một khoảng
Vận dụng
c) Dựa vào tính đơn điệu của hàm số để chứng minh bất đẳng thức. 
Vận dụng
2
Cực trị của hàm số
3.5
Tìm điểm cực trị của hàm số
Thông hiểu
Tính yCĐ, yCT
Thông hiểu
Xác định tham số để hàm số đạt cực trị tại điểm x0
Vận dụng
3
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
Tìm GTLN, GTNN của hàm số trên 1 khoảng 1 đoạn, một tập cho trước, trên TXĐ
Thông hiểu
Ứng dụng để giải phương trình, bất phương trình
Vận dụng
4
Đường tiệm cận
1.5
 Tìm tiệm cận đứng và tiệm cận ngang của đồ thị
Vận dụng
KIỂM TRA 
Môn: Giải tích 12 (tiết 18)
 Thời gian: 45’ 
ĐỀ 1
Câu 1 (3.5 điểm): Xét tính đồng biến, nghịch biến và tìm cực trị (nếu có) của các hàm số sau:
	a) 	b) .
Câu 2 (3.0 điểm) Tìm giá trị lớn nhất, nhỏ nhất của các hàm số sau:
	a) trên 	b) trên 
Câu 3 (1.5 điểm) Tìm tiệm cận đứng và tiệm cận ngang của hàm số sau: 
.
Câu 4 (2.0 điểm) Chứng minh rằng với mọi giá trị của m hàm số luôn có cực đại và cực tiểu.
----------- Hết ----------
Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên:........................................................................; Lớp:...........................
KIỂM TRA 
Môn: Giải tích 12 (tiết 18)
 Thời gian: 45’ 
ĐỀ 2
Câu 1 (3.5 điểm): Xét tính đồng biến, nghịch biến và tìm cực trị (nếu có) của các hàm số sau:
	a) 	b) 
Câu 2 (3.0 điểm) Tìm giá trị lớn nhất, nhỏ nhất của các hàm số sau:
	a) trên 	b) trên 
Câu 3 (1.5 điểm) Tìm tiệm cận đứng và tiệm cận ngang của hàm số sau: 
.
Câu 4 (2.0 điểm) Chứng minh rằng với mọi giá trị của m hàm số luôn có cực đại và cực tiểu.
----------- Hết ----------
Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên:........................................................................; Lớp:...........................
KIỂM TRA 
Môn: Giải tích 12 (tiết 18)
 Thời gian: 45’ 
ĐỀ 3
Câu 1 (3.5 điểm): Xét tính đồng biến, nghịch biến và tìm cực trị (nếu có) của các hàm số sau:
	a) 	b) 
Câu 2 (3.0 điểm) Tìm giá trị lớn nhất, nhỏ nhất của các hàm số sau:
	a) trên 	b) trên 
Câu 3 (1.5 điểm) Tìm tiệm cận đứng và tiệm cận ngang của hàm số sau: 
.
Câu 4 (2.0 điểm) Chứng minh rằng với mọi giá trị của m hàm số luôn có cực đại và cực tiểu.
----------- Hết ----------
Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên:........................................................................; Lớp:...........................
HƯỚNG DẪN CHẤM 
Môn: Giải tích 12 
(tiết 18)
ĐỀ 1
Bài
ý
Nội dung
Điểm
1
(3,5đ)
a
(2đ)
TXĐ: D = R
Hàm số ĐB trên khoảng 
Hàm số nghịch biến trên các khoảng và 
0,25
0,25
0,5
0,5
0,25
0,25
b
(1,5đ)
TXĐ: D = R\{2}
Hàm số ĐB trên các khoảng và 
0,25
1
0,25
2
(3đ)
a
(1,5đ)
TXĐ: D = R
0,25
0,25
0,5
0,25
0,25
b 
(1,5đ)
TXĐ: 
BBT
x
- ∞ -2 0 2 +∞
y’
 - 0 + + 0 -
y
 - 4
 - ∞ -∞
 không có
0,25
0,5
0,5
0,25
3
(1,5đ)
 Tiệm cận ngang là đt y = -3
 Tiệm cận đứng là đường thẳng x = 2
0,75
0,75
4
(2đ)
TXĐ: D = R\{m}
Ta thấy x = m không là nghiệm pt (1) và ∆ = 1 > 0
y’ luôn có 2 nghiệm phân biệt 
hàm số luôn có CT – CĐ 
0,5
0,5
0,5
0,5
--------------------------------Hết------------------------------
HƯỚNG DẪN CHẤM 
Môn: Giải tích 12 
(tiết 18)
ĐỀ 2
Bài
ý
Nội dung
Điểm
1
(3,5đ)
a
(2đ)
TXĐ: D = R 
Hàm số NB trên khoảng 
Hàm số ĐB trên các khoảng và 
0,25
0,25
0,5
0,5
0,5
b
(1,5đ)
TXĐ: D = R\{2}
Hàm số ĐB trên các khoảng và 
0,25
1
0,25
2
(3đ)
a
(1,5đ)
TXĐ: D = R
0,25
0,25
0,5
0,25
0,25
b 
(1,5đ)
TXĐ: 
BBT
x
- ∞ -2 0 2 +∞
y’
 - 0 + + 0 -
y
 - 4
 - ∞ -∞
 không có
0,25
0,5
0,5
0,25
3
(1,5đ)
 Tiệm cận ngang là đt y = 5
 Tiệm cận đứng là đt x = 2
0,75
0,75
4
(2đ)
TXĐ: D = R\{m};
Ta thấy x = m không là nghiệm pt (1) và ∆ = 1 > 0
y’ luôn có 2 nghiệm phân biệt 
hàm số luôn có CT – CĐ 
0,5
0,5
0,5
0,5
--------------------------------Hết------------------------------
HƯỚNG DẪN CHẤM 
Môn: Giải tích 12 
(tiết 18)
ĐỀ 3
Bài
ý
Nội dung
Điểm
1
(3,5đ)
a
(2đ)
TXĐ: D = R 
Hàm số NB trên khoảng 
Hàm số ĐB trên các khoảng và 
0,25
0,25
0,5
0,5
0,5
b
(1,5đ)
TXĐ: D = R\
Hàm số NB trên các khoảng và 
0,25
1
0,25
2
(3đ)
a
(1,5đ)
TXĐ: D = R
0,25
0,25
0,5
0,25
0,25
b 
(1,5đ)
TXĐ: 
BBT
x
- ∞ -3 0 3 +∞
y’
 - 0 + + 0 -
y
+∞ +∞ 
 6 
 không có
0,25
0,5
0,5
0,25
3
(1,5đ)
 Tiệm cận ngang là đt y = 4
 Tiệm cận đứng là đt x = -3
0,75
0,75
4
(2đ)
TXĐ: D = R\{m};
Ta thấy x = m không là nghiệm pt (1) và ∆ = 1 > 0
y’ luôn có 2 nghiệm phân biệt 
hàm số luôn có CT – CĐ 
0,5
0,5
0,5
0,5
--------------------------------Hết------------------------------