Kiểm tra học kì II môn: Toán số - Lớp 11

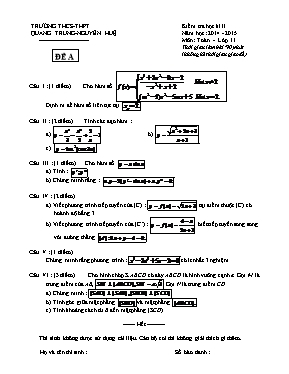
 TRƯỜNG THCS-THPT 	Kiểm tra học kì II
 QUANG TRUNG-NGUYỄN HUỆ 	Năm học: 2014 - 2015
 ------------------------- 	Môn: Toán - Lớp 11
ĐỀ A
 	Thời gian làm bài: 90 phút 
(không kể thời gian giao đề)
Câu I : (1 điểm) Cho hàm số 
	Định m để hàm số liên tục tại 
Câu II : (2 điểm) Tính các đạo hàm :
	a) 	b) 
	c) 	 
Câu III : (1 điểm) Cho hàm số 
	a) Tính : . 	
	b) Chứng minh rằng : 
Câu IV : (2 điểm) 
	a) Viết phương trình tiếp tuyến của (C) : tại điểm thuộc (C) có 
	 hoành độ bằng 3.
	b) Viết phương trình tiếp tuyến của (C’) : biết tiếp tuyến song song 
	 với đường thẳng 
Câu V : (1 điểm) 
Chứng minh rằng phương trình : có ít nhất 3 nghiệm
Câu VI : (3 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M là 
	trung điểm của AB, . Gọi N là trung điểm CD.
	a) Chứng minh : .
	b) Tính góc giữa mặt phẳng và mặt phẳng 
	c) Tính khoảng cách từ B đến mặt phẳng (SCD).
------ Hết ---------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
 Họ và tên thí sinh : .Số báo danh : 
TRƯỜNG THCS-THPT 	Kiểm tra học kì II
 QUANG TRUNG-NGUYỄN HUỆ 	Năm học: 2014 - 2015
 ------------------------- 	Môn: Toán - Lớp 11
ĐỀ B
 	Thời gian làm bài: 90 phút 
(không kể thời gian giao đề)
Câu I : (1 điểm) Cho hàm số 
	Định m để hàm số liên tục tại 
Câu II : (2 điểm) Tính các đạo hàm :
	a) 	b) 
	c) 
Câu III : (1 điểm) Cho hàm số 
	a) Tính : . 	
	b) Chứng minh rằng : 
Câu IV : (2 điểm) 
	a) Viết phương trình tiếp tuyến của (C) : tại điểm thuộc (C) có 
	 hoành độ bằng 2.
	b) Viết phương trình tiếp tuyến của (C’) : biết tiếp tuyến song song 
	 với đường thẳng 
Câu V : (1 điểm) 
Chứng minh rằng phương trình : có ít nhất 3 nghiệm
Câu VI : (3 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi I là 
	trung điểm của AB, . Gọi J là trung điểm CD.
	a) Chứng minh : .
	b) Tính góc giữa mặt phẳng và mặt phẳng 
	c) Tính khoảng cách từ A đến mặt phẳng (SCD).
------ Hết ---------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
 Họ và tên thí sinh : .Số báo danh : 
HƯỚNG DẪN CHẤM TOÁN HỌC KỲ II – LỚP 11 – NĂM HỌC 2014-2015
ĐỀ A
ĐIỂM
ĐỀ B
CÂU I :
1 đ
CÂU I : 
Để hàm số liên tục tại x0=2 thì 
0,25
0,5
0,25
Để hàm số liên tục tại x0=2 thì 
CÂU II : Tính đạo hàm
2 đ
CÂU II : Tính đạo hàm
a) 
0,5 đ
0,5
a) 
b) 
0,75đ
0,25
0,25
0,25
b) 
c) 
0,75đ
0,25
0,5
c) 
CÂU III : Cho hàm số 
1 đ
CÂU III : Cho hàm số 
a) Tính : . 
0,5đ
0,25
0,25
a) Tính : . 	
y'=cosx-xsinx	 
b) CMR : 
VT= x.y-2y'-sinx+ x.y''
=x.xsinx-2sinx+xcosx-sinx+x.(2cosx-xsinx)
=x2sinx-2xcosx+2xcosx-x2sinx
=0=VP (đpcm)
0,5đ
0,25
0,25
b) CMR : 
T= x.y-2y'-cosx+ x.y''
=x.xcosx-2cosx-xsinx-cosx
+x.(-2sinx-xcosx)
=x2cosx+2xsinx-2xsinx-x2cosx
=0=0=VP (đpcm)
CÂU IV :
2 đ
CÂU IV :
a) Viết phương trình tiếp tuyến của (C) : tại điểm thuộc (C) có 
	 hoành độ bằng 3.
Phương trình tiếp tuyến tại M(3;3) là :
1 đ
0,25
0,25
0,25
0,25
a) Viết phương trình tiếp tuyến của (C) : tại điểm thuộc (C) có 
	 hoành độ bằng 2.
Phương trình tiếp tuyến tại M(2;3) là :
b) Viết phương trình tiếp tuyến của (C’) : biết tiếp tuyến song song 
	 với đường thẳng 
* * 
* Tiếp điểm , tt // (d) :
 Phương trình tiếp tuyến tại M(0;4) là :(loại)
 Phương trình tiếp tuyến tại M(-1;-5) là :
1 đ
0,25
0,25
0,25
0,25
b) Viết phương trình tiếp tuyến của (C’) : biết tiếp tuyến song song 
	 với đường thẳng 
* * 
* Tiếp điểm , tt // (d) :
 Phương trình tiếp tuyến tại M(0;3) là :(loại)
 Phương trình tiếp tuyến tại M(-1;-4) là :
CÂU V :
1 đ
CÂU V :
Chứng minh rằng phương trình : có ít nhất 3 nghiệm
* Xét hàm số fx=x5-3x4+ 5x-2 
 liên tục trên R.
* phương trình có ít nhất 1 nghiệm 
* ..
* Kết luận .
0,25
0,25
0,25
Chứng minh rằng phương trình : có ít nhất 3 nghiệm
* Xét hàm số fx=x5-3x-1 
 liên tục trên R.
* phương trình có ít nhất 1 nghiệm 
* ..
* Kết luận .
CÂU VI :
3 đ
CÂU VI :
Hình vẽ
0,25
Hình vẽ
a) Chứng minh : 
* Ta có:
Þ AD ^ (SAB)
Mà AD Ì (SAD)
Þ (SAD) ^ (SAB) 
* Ta có:
Þ CD ^ (SMN)
 Mà CD Ì (SCD)
Þ (SCD) ^ (SMN)
1 đ
0,25
0,25
0,25
0,25
a) Chứng minh : 
Ta có:
Þ BC ^ (SAB)
 Mà BC Ì (SBC)
Þ (SBC) ^ (SAB) 
* Ta có:
Þ CD ^ (SIJ)
 Mà CD Ì (SCD)
Þ (SCD) ^ (SIJ)
b) Tính góc giữa mặt phẳng và mặt phẳng 
Kẻ MH^BD tại H
Chứng minh được
 Tính được:
0,75 đ
0,25
0,25
0,25
b) Tính góc giữa mặt phẳng và mặt phẳng 
Kẻ MH^AC tại H
 Chứng minh được
 Tính được:
c) Tính khoảng cách tứ B đến mặt phẳng (SCD).
Kẻ MK^SN tại K
Chứng minh được d(M,(SCD) = MK
Tính được 
Ta có BM//CDÞBM//(SCD)
d(M, (SCD)) = d(M, (SCD))= 
0,75 đ
0,25
0,25
0,25
c) Tính khoảng cách tứ A đến mặt phẳng (SCD).
Kẻ IK^SJ tại K
Chứng minh được d(I,(SCD) = IK
Tính được 
Ta có AI//ICDÞA//(SCD)
d(I, (SCD)) = d(A, (SCD))=