Kiểm tra giải tích 12 - Ứng dụng tích phân và số phức - Mã đề: 100

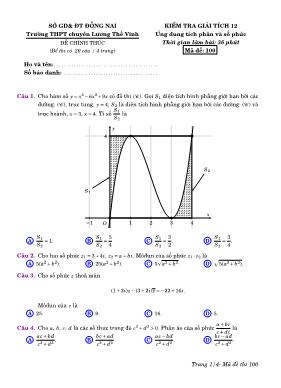
SỞ GD& ĐT ĐỒNG NAI
Trường THPT chuyên Lương Thế Vinh
ĐỀ CHÍNH THỨC
(Đề thi có 20 câu / 4 trang)
KIỂM TRA GIẢI TÍCH 12
Ứng dụng tích phân và số phức
Thời gian làm bài: 36 phút
Mã đề: 100
Họ và tên:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. Cho hàm số y= x3−6x2+9x có đồ thị (C ). Gọi S1 diện tích hình phẳng giới hạn bởi các
đường: (C ), trục tung, y= 4; S2 là diện tích hình phẳng giới hạn bởi các đường: (C ) và
trục hoành, x= 3, x= 4. Tỉ số S1
S2
là
−1 1 2 3 4
4
O
S2
S1
x
y
A
S1
S2
= 1. B S1
S2
= 5
4
C
S1
S2
= 3
2
. D
S1
S2
= 3
4
.
Câu 2. Cho hai số phức z1 = 3+4i, z2 = a+bi. Môđun của số phức z1 · z2 là
A 5(a2+b2). B 25(a2+b2). C 5
p
a2+b2. D
√
5(a2+b2).
Câu 3. Cho số phức z thoả mãn
(1+2i)z− (3+2i)z=−22+16i.
Môđun của z là
A 25. B 9. C 16. D 5.
Câu 4. Cho a, b, c, d là các số thực trong đó c2+d2 > 0. Phần ảo của số phức a+bi
c+di là
A
ac+bd
c2+d2 . B
bc+ad
c2+d2 . C
ac−bd
c2+d2 . D
bc−ad
c2+d2 .
Trang 1/4- Mã đề thi 100
Câu 5. Cho số phức z thoả mãn
(z− i)(1+ i)=−2+8i.
Phần ảo của z là
A −4i. B 3. C −4. D 4.
Câu 6. Tập hợp các điểm biểu diễn số phức z thoả |z−3+ i| = 2 là
A đường tròn tâm I(3;−1) bán kính bằng 2. B đường tròn tâm I(3;−1) bán kính bằng 4 .
C đường tròn tâm I(−3;1) bán kính bằng 2. D đường tròn tâm I(−3;1) bán kính bằng 4.
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=
p
1− x2 và trục hoành là
A
pi
4
. B
pi
2
. C pi. D 2pi.
Câu 8. Gọi (H ) là hình phẳng giới hạn bởi các đường thẳng y= x+1, x= 4, hai trục toạ độ và
a, b là hai số thực thoả 0< a< b< 4.
4
5
O
y=
x+
1
x
=
a
x
=
b
a b
x
y
Giá trị của a+ b để hai đường thẳng x = a và x = b chia hình (H ) thành ba phần có
diện tích bằng nhau là
A 3+p17. B 1. C −1+p17. D 1+p17.
Câu 9. Cho hàm số y= f (x) có đồ thị (C ) như hình vẽ dưới đây. Gọi S là diện tích hình phẳng
giới hạn bởi (C ), hai trục toạ độ và đường thẳng x= 2. Khẳng định nào sau đây đúng?
−1 1 3O
2
2
−2
x
y
A S =
∫ 1
0
f (x)dx−
∫ 2
1
f (x)dx.
B S =
∫ 1
0
f (x)dx+
∫ 2
1
f (x)dx.
C S =
∫ 2
0
f (x)dx.
D S =
∣∣∣∣∫ 2
0
f (x)dx
∣∣∣∣.
Trang 2/4- Mã đề thi 100
Câu 10. Gọi z1, z2 là hai nghiệm phức của phương trình z2−6z+25= 0. Giá trị của
∣∣z31∣∣+ ∣∣z32∣∣ là
A 125. B 250. C 50. D 6750.
Câu 11. Cho số phức z thoả mãn z · (1+2i)= 1−3i. Điểm biểu diễn cho z là
A B(−1;−1) . B A(−1;1). C C(1;1) . D D(1;−1).
Câu 12. Môđun của số phức z= i2016+ i2017 là
A
p
2. B 1. C 2. D 0.
Câu 13. Diện tích S của hình phẳng giới hạn bởi đường parabol y = x2−3x+2 và hai đường
thẳng y= x−1, x= 0 là
A S = 3
8
. B S = 0. C S = 4
3
. D S = 8
3
.
Câu 14. Tập hợp các điểm trên mặt phẳng toạ độ biểu diễn các số phức z sao cho số phức
w= z(1+2i)+ (3+4i) là số thuần ảo là
A đường thẳng 2x+ y+4= 0. B điểm
(
−11
5
;
2
5
)
.
C đường thẳng x+2y+3= 0. D đường thẳng x−2y+3= 0.
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = p−8x−7 và đường thẳng
y=−2x−1 được biểu diễn dưới dạng a
b
, trong đó a, b là các số tự nhiên và phân số
a
b
tối giản. Giá trị của a+b là
A 5. B 6. C 7. D 8.
Câu 16. Trong mặt phẳng phức Oxy, gọi M là điểm biểu diễn cho số phức z và M′ là điểm biểu
diễn cho số phức liên hợp của z. Khẳng định nào sau đây đúng?
A M và M′ đối xứng nhau qua trục tung.
B M và M′ đối xứng nhau qua gốc toạ độ.
C M và M′ đối xứng nhau qua trục hoành.
D M và M′ đối xứng nhau qua đường phân giác thứ nhất.
Câu 17. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các
đường y= cotx, y= 0, x= pi
4
, x= pi
2
là
A pi
(
1− pi
4
)
. B
pi2
4
. C pi
(
1+ pi
4
)
. D
3pi2
4
.
Câu 18. Cho hàm số y = f (x) liên tục trên đoạn [a;b] có đồ thị là (C ). Gọi (H ) là hình phẳng
giới hạn bởi (C ), trục hoành và hai đường thẳng x= a, x= b. Diện tích của (H ) là
A S =
∣∣∣∣∫ b
a
f (x)dx
∣∣∣∣. B S = ∫ b
a
f (x)dx. C S =
∫ b
a
| f (x)|dx. D S =−
∫ b
a
f (x)dx.
Câu 19. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các
đường y= x ·
√
ex3, y= 0, x= 0, x= 1 được viết dưới dạng pi(a+be) trong đó a, b là các số
hữu tỉ. Giá trị của tích a ·b là
A
1
9
. B −1
9
. C
1
3
. D
1
27
.
Trang 3/4- Mã đề thi 100
Câu 20. Cho a là số thực dương. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của hàm số
y= x3, trục hoành và hai đường thẳng x=−a và x= a. Khẳng định nào sau đây sai?
O
−a
a
y=
x3
x
y
A S =
∫ a
0
x3dx−
∫ 0
−a
x3dx. B S =
∣∣∣∣∫ a−a x3dx
∣∣∣∣.
C S =
∫ a
−a
∣∣x3∣∣dx. D S = 2∫ a
0
x3dx.
—- HẾT—-
Trang 4/4- Mã đề thi 100
Mã đề thi 100 ĐÁP ÁN
Câu 1. A
Câu 2. C
Câu 3. D
Câu 4. D
Câu 5. C
Câu 6. A
Câu 7. B
Câu 8. D
Câu 9. A
Câu 10. B
Câu 11. B
Câu 12. A
Câu 13. D
Câu 14. D
Câu 15. C
Câu 16. C
Câu 17. A
Câu 18. C
Câu 19. B
Câu 20. B
Trang 1/4- Mã đề thi 100
SỞ GD& ĐT ĐỒNG NAI
Trường THPT chuyên Lương Thế Vinh
ĐỀ CHÍNH THỨC
(Đề thi có 20 câu / 4 trang)
KIỂM TRA GIẢI TÍCH 12
Ứng dụng tích phân và số phức
Thời gian làm bài: 36 phút
Mã đề: 101
Họ và tên:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. Cho số phức z thoả mãn z · (1+2i)= 1−3i. Điểm biểu diễn cho z là
A D(1;−1). B B(−1;−1) . C A(−1;1). D C(1;1) .
Câu 2. Cho số phức z thoả mãn
(z− i)(1+ i)=−2+8i.
Phần ảo của z là
A 4. B −4i. C 3. D −4.
Câu 3. Môđun của số phức z= i2016+ i2017 là
A 0. B
p
2. C 1. D 2.
Câu 4. Cho hàm số y= x3−6x2+9x có đồ thị (C ). Gọi S1 diện tích hình phẳng giới hạn bởi các
đường: (C ), trục tung, y= 4; S2 là diện tích hình phẳng giới hạn bởi các đường: (C ) và
trục hoành, x= 3, x= 4. Tỉ số S1
S2
là
−1 1 2 3 4
4
O
S2
S1
x
y
A
S1
S2
= 3
4
. B
S1
S2
= 1. C S1
S2
= 5
4
D
S1
S2
= 3
2
.
Câu 5. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=
p
1− x2 và trục hoành là
A 2pi. B
pi
4
. C
pi
2
. D pi.
Trang 1/4- Mã đề thi 101
Câu 6. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = p−8x−7 và đường thẳng
y=−2x−1 được biểu diễn dưới dạng a
b
, trong đó a, b là các số tự nhiên và phân số
a
b
tối giản. Giá trị của a+b là
A 8. B 5. C 6. D 7.
Câu 7. Cho hàm số y = f (x) liên tục trên đoạn [a;b] có đồ thị là (C ). Gọi (H ) là hình phẳng
giới hạn bởi (C ), trục hoành và hai đường thẳng x= a, x= b. Diện tích của (H ) là
A S =−
∫ b
a
f (x)dx. B S =
∣∣∣∣∫ b
a
f (x)dx
∣∣∣∣. C S = ∫ b
a
f (x)dx. D S =
∫ b
a
| f (x)|dx.
Câu 8. Cho số phức z thoả mãn
(1+2i)z− (3+2i)z=−22+16i.
Môđun của z là
A 5. B 25. C 9. D 16.
Câu 9. Trong mặt phẳng phức Oxy, gọi M là điểm biểu diễn cho số phức z và M′ là điểm biểu
diễn cho số phức liên hợp của z. Khẳng định nào sau đây đúng?
A M và M′ đối xứng nhau qua đường phân giác thứ nhất.
B M và M′ đối xứng nhau qua trục tung.
C M và M′ đối xứng nhau qua gốc toạ độ.
D M và M′ đối xứng nhau qua trục hoành.
Câu 10. Tập hợp các điểm trên mặt phẳng toạ độ biểu diễn các số phức z sao cho số phức
w= z(1+2i)+ (3+4i) là số thuần ảo là
A đường thẳng x−2y+3= 0. B đường thẳng 2x+ y+4= 0.
C điểm
(
−11
5
;
2
5
)
. D đường thẳng x+2y+3= 0.
Trang 2/4- Mã đề thi 101
Câu 11. Cho a là số thực dương. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của hàm số
y= x3, trục hoành và hai đường thẳng x=−a và x= a. Khẳng định nào sau đây sai?
O
−a
a
y=
x3
x
y
A S = 2
∫ a
0
x3dx. B S =
∫ a
0
x3dx−
∫ 0
−a
x3dx.
C S =
∣∣∣∣∫ a−a x3dx
∣∣∣∣. D S = ∫ a−a ∣∣x3∣∣dx.
Câu 12. Gọi z1, z2 là hai nghiệm phức của phương trình z2−6z+25= 0. Giá trị của
∣∣z31∣∣+ ∣∣z32∣∣ là
A 6750. B 125. C 250. D 50.
Câu 13. Cho hàm số y= f (x) có đồ thị (C ) như hình vẽ dưới đây. Gọi S là diện tích hình phẳng
giới hạn bởi (C ), hai trục toạ độ và đường thẳng x= 2. Khẳng định nào sau đây đúng?
−1 1 3O
2
2
−2
x
y
A S =
∣∣∣∣∫ 2
0
f (x)dx
∣∣∣∣.
B S =
∫ 1
0
f (x)dx−
∫ 2
1
f (x)dx.
C S =
∫ 1
0
f (x)dx+
∫ 2
1
f (x)dx.
D S =
∫ 2
0
f (x)dx.
Trang 3/4- Mã đề thi 101
Câu 14. Gọi (H ) là hình phẳng giới hạn bởi các đường thẳng y= x+1, x= 4, hai trục toạ độ và
a, b là hai số thực thoả 0< a< b< 4.
4
5
O
y=
x+
1
x
=
a
x
=
b
a b
x
y
Giá trị của a+ b để hai đường thẳng x = a và x = b chia hình (H ) thành ba phần có
diện tích bằng nhau là
A 1+p17. B 3+p17. C 1. D −1+p17.
Câu 15. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các
đường y= cotx, y= 0, x= pi
4
, x= pi
2
là
A
3pi2
4
. B pi
(
1− pi
4
)
. C
pi2
4
. D pi
(
1+ pi
4
)
.
Câu 16. Cho hai số phức z1 = 3+4i, z2 = a+bi. Môđun của số phức z1 · z2 là
A
√
5(a2+b2). B 5(a2+b2). C 25(a2+b2). D 5
p
a2+b2.
Câu 17. Tập hợp các điểm biểu diễn số phức z thoả |z−3+ i| = 2 là
A đường tròn tâm I(−3;1) bán kính bằng 4. B đường tròn tâm I(3;−1) bán kính bằng 2.
C đường tròn tâm I(3;−1) bán kính bằng 4 . D đường tròn tâm I(−3;1) bán kính bằng 2.
Câu 18. Cho a, b, c, d là các số thực trong đó c2+d2 > 0. Phần ảo của số phức a+bi
c+di là
A
bc−ad
c2+d2 . B
ac+bd
c2+d2 . C
bc+ad
c2+d2 . D
ac−bd
c2+d2 .
Câu 19. Diện tích S của hình phẳng giới hạn bởi đường parabol y = x2−3x+2 và hai đường
thẳng y= x−1, x= 0 là
A S = 8
3
. B S = 3
8
. C S = 0. D S = 4
3
.
Câu 20. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các
đường y= x ·
√
ex3, y= 0, x= 0, x= 1 được viết dưới dạng pi(a+be) trong đó a, b là các số
hữu tỉ. Giá trị của tích a ·b là
A
1
27
. B
1
9
. C −1
9
. D
1
3
.
Trang 4/4- Mã đề thi 101
—- HẾT—-
Trang 5/4- Mã đề thi 101
Mã đề thi 101 ĐÁP ÁN
Câu 1. C
Câu 2. D
Câu 3. B
Câu 4. B
Câu 5. C
Câu 6. D
Câu 7. D
Câu 8. A
Câu 9. D
Câu 10. A
Câu 11. C
Câu 12. C
Câu 13. B
Câu 14. A
Câu 15. B
Câu 16. D
Câu 17. B
Câu 18. A
Câu 19. A
Câu 20. C
Trang 1/4- Mã đề thi 101
SỞ GD& ĐT ĐỒNG NAI
Trường THPT chuyên Lương Thế Vinh
ĐỀ CHÍNH THỨC
(Đề thi có 20 câu / 4 trang)
KIỂM TRA GIẢI TÍCH 12
Ứng dụng tích phân và số phức
Thời gian làm bài: 36 phút
Mã đề: 102
Họ và tên:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. Cho số phức z thoả mãn
(1+2i)z− (3+2i)z=−22+16i.
Môđun của z là
A 25. B 5. C 9. D 16.
Câu 2. Cho hàm số y = f (x) liên tục trên đoạn [a;b] có đồ thị là (C ). Gọi (H ) là hình phẳng
giới hạn bởi (C ), trục hoành và hai đường thẳng x= a, x= b. Diện tích của (H ) là
A S =
∣∣∣∣∫ b
a
f (x)dx
∣∣∣∣. B S =−∫ b
a
f (x)dx. C S =
∫ b
a
f (x)dx. D S =
∫ b
a
| f (x)|dx.
Câu 3. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các
đường y= x ·
√
ex3, y= 0, x= 0, x= 1 được viết dưới dạng pi(a+be) trong đó a, b là các số
hữu tỉ. Giá trị của tích a ·b là
A
1
9
. B
1
27
. C −1
9
. D
1
3
.
Câu 4. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = p−8x−7 và đường thẳng
y=−2x−1 được biểu diễn dưới dạng a
b
, trong đó a, b là các số tự nhiên và phân số
a
b
tối giản. Giá trị của a+b là
A 5. B 8. C 6. D 7.
Trang 1/4- Mã đề thi 102
Câu 5. Cho hàm số y= x3−6x2+9x có đồ thị (C ). Gọi S1 diện tích hình phẳng giới hạn bởi các
đường: (C ), trục tung, y= 4; S2 là diện tích hình phẳng giới hạn bởi các đường: (C ) và
trục hoành, x= 3, x= 4. Tỉ số S1
S2
là
−1 1 2 3 4
4
O
S2
S1
x
y
A
S1
S2
= 1. B S1
S2
= 3
4
. C
S1
S2
= 5
4
D
S1
S2
= 3
2
.
Câu 6. Cho hai số phức z1 = 3+4i, z2 = a+bi. Môđun của số phức z1 · z2 là
A 5(a2+b2). B
√
5(a2+b2). C 25(a2+b2). D 5
p
a2+b2.
Câu 7. Tập hợp các điểm trên mặt phẳng toạ độ biểu diễn các số phức z sao cho số phức
w= z(1+2i)+ (3+4i) là số thuần ảo là
A đường thẳng 2x+ y+4= 0. B đường thẳng x−2y+3= 0.
C điểm
(
−11
5
;
2
5
)
. D đường thẳng x+2y+3= 0.
Câu 8. Cho số phức z thoả mãn z · (1+2i)= 1−3i. Điểm biểu diễn cho z là
A B(−1;−1) . B D(1;−1). C A(−1;1). D C(1;1) .
Câu 9. Cho số phức z thoả mãn
(z− i)(1+ i)=−2+8i.
Phần ảo của z là
A −4i. B 4. C 3. D −4.
Câu 10. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các
đường y= cotx, y= 0, x= pi
4
, x= pi
2
là
A pi
(
1− pi
4
)
. B
3pi2
4
. C
pi2
4
. D pi
(
1+ pi
4
)
.
Câu 11. Cho a, b, c, d là các số thực trong đó c2+d2 > 0. Phần ảo của số phức a+bi
c+di là
A
ac+bd
c2+d2 . B
bc−ad
c2+d2 . C
bc+ad
c2+d2 . D
ac−bd
c2+d2 .
Trang 2/4- Mã đề thi 102
Câu 12. Cho a là số thực dương. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của hàm số
y= x3, trục hoành và hai đường thẳng x=−a và x= a. Khẳng định nào sau đây sai?
O
−a
a
y=
x3
x
y
A S =
∫ a
0
x3dx−
∫ 0
−a
x3dx. B S = 2
∫ a
0
x3dx.
C S =
∣∣∣∣∫ a−a x3dx
∣∣∣∣. D S = ∫ a−a ∣∣x3∣∣dx.
Câu 13. Gọi z1, z2 là hai nghiệm phức của phương trình z2−6z+25= 0. Giá trị của
∣∣z31∣∣+ ∣∣z32∣∣ là
A 125. B 6750. C 250. D 50.
Câu 14. Gọi (H ) là hình phẳng giới hạn bởi các đường thẳng y= x+1, x= 4, hai trục toạ độ và
a, b là hai số thực thoả 0< a< b< 4.
4
5
O
y=
x+
1
x
=
a
x
=
b
a b
x
y
Giá trị của a+ b để hai đường thẳng x = a và x = b chia hình (H ) thành ba phần có
diện tích bằng nhau là
A 3+p17. B 1+p17. C 1. D −1+p17.
Trang 3/4- Mã đề thi 102
Câu 15. Tập hợp các điểm biểu diễn số phức z thoả |z−3+ i| = 2 là
A đường tròn tâm I(3;−1) bán kính bằng 2. B đường tròn tâm I(−3;1) bán kính bằng 4.
C đường tròn tâm I(3;−1) bán kính bằng 4 . D đường tròn tâm I(−3;1) bán kính bằng 2.
Câu 16. Môđun của số phức z= i2016+ i2017 là
A
p
2. B 0. C 1. D 2.
Câu 17. Trong mặt phẳng phức Oxy, gọi M là điểm biểu diễn cho số phức z và M′ là điểm biểu
diễn cho số phức liên hợp của z. Khẳng định nào sau đây đúng?
A M và M′ đối xứng nhau qua trục tung.
B M và M′ đối xứng nhau qua đường phân giác thứ nhất.
C M và M′ đối xứng nhau qua gốc toạ độ.
D M và M′ đối xứng nhau qua trục hoành.
Câu 18. Diện tích S của hình phẳng giới hạn bởi đường parabol y = x2−3x+2 và hai đường
thẳng y= x−1, x= 0 là
A S = 3
8
. B S = 8
3
. C S = 0. D S = 4
3
.
Câu 19. Cho hàm số y= f (x) có đồ thị (C ) như hình vẽ dưới đây. Gọi S là diện tích hình phẳng
giới hạn bởi (C ), hai trục toạ độ và đường thẳng x= 2. Khẳng định nào sau đây đúng?
−1 1 3O
2
2
−2
x
y
A S =
∫ 1
0
f (x)dx−
∫ 2
1
f (x)dx.
B S =
∣∣∣∣∫ 2
0
f (x)dx
∣∣∣∣.
C S =
∫ 1
0
f (x)dx+
∫ 2
1
f (x)dx.
D S =
∫ 2
0
f (x)dx.
Câu 20. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=
p
1− x2 và trục hoành là
A
pi
4
. B 2pi. C
pi
2
. D pi.
—- HẾT—-
Trang 4/4- Mã đề thi 102
Mã đề thi 102 ĐÁP ÁN
Câu 1. B
Câu 2. D
Câu 3. C
Câu 4. D
Câu 5. A
Câu 6. D
Câu 7. B
Câu 8. C
Câu 9. D
Câu 10. A
Câu 11. B
Câu 12. C
Câu 13. C
Câu 14. B
Câu 15. A
Câu 16. A
Câu 17. D
Câu 18. B
Câu 19. A
Câu 20. C
Trang 1/4- Mã đề thi 102
SỞ GD& ĐT ĐỒNG NAI
Trường THPT chuyên Lương Thế Vinh
ĐỀ CHÍNH THỨC
(Đề thi có 20 câu / 4 trang)
KIỂM TRA GIẢI TÍCH 12
Ứng dụng tích phân và số phức
Thời gian làm bài: 36 phút
Mã đề: 103
Họ và tên:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. Môđun của số phức z= i2016+ i2017 là
A
p
2. B 2. C 1. D 0.
Câu 2. Tập hợp các điểm trên mặt phẳng toạ độ biểu diễn các số phức z sao cho số phức
w= z(1+2i)+ (3+4i) là số thuần ảo là
A đường thẳng 2x+ y+4= 0. B đường thẳng x+2y+3= 0.
C điểm
(
−11
5
;
2
5
)
. D đường thẳng x−2y+3= 0.
Câu 3. Cho số phức z thoả mãn
(1+2i)z− (3+2i)z=−22+16i.
Môđun của z là
A 25. B 16. C 9. D 5.
Câu 4. Trong mặt phẳng phức Oxy, gọi M là điểm biểu diễn cho số phức z và M′ là điểm biểu
diễn cho số phức liên hợp của z. Khẳng định nào sau đây đúng?
A M và M′ đối xứng nhau qua trục tung.
B M và M′ đối xứng nhau qua trục hoành.
C M và M′ đối xứng nhau qua gốc toạ độ.
D M và M′ đối xứng nhau qua đường phân giác thứ nhất.
Câu 5. Cho a, b, c, d là các số thực trong đó c2+d2 > 0. Phần ảo của số phức a+bi
c+di là
A
ac+bd
c2+d2 . B
ac−bd
c2+d2 . C
bc+ad
c2+d2 . D
bc−ad
c2+d2 .
Câu 6. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các
đường y= x ·
√
ex3, y= 0, x= 0, x= 1 được viết dưới dạng pi(a+be) trong đó a, b là các số
hữu tỉ. Giá trị của tích a ·b là
A
1
9
. B
1
3
. C −1
9
. D
1
27
.
Trang 1/4- Mã đề thi 103
Câu 7. Gọi (H ) là hình phẳng giới hạn bởi các đường thẳng y= x+1, x= 4, hai trục toạ độ và
a, b là hai số thực thoả 0< a< b< 4.
4
5
O
y=
x+
1
x
=
a
x
=
b
a b
x
y
Giá trị của a+ b để hai đường thẳng x = a và x = b chia hình (H ) thành ba phần có
diện tích bằng nhau là
A 3+p17. B −1+p17. C 1. D 1+p17.
Câu 8. Cho a là số thực dương. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của hàm số
y= x3, trục hoành và hai đường thẳng x=−a và x= a. Khẳng định nào sau đây sai?
O
−a
a
y=
x3
x
y
A S =
∫ a
0
x3dx−
∫ 0
−a
x3dx. B S =
∫ a
−a
∣∣x3∣∣dx.
C S =
∣∣∣∣∫ a−a x3dx
∣∣∣∣. D S = 2∫ a
0
x3dx.
Trang 2/4- Mã đề thi 103
Câu 9. Cho hàm số y= x3−6x2+9x có đồ thị (C ). Gọi S1 diện tích hình phẳng giới hạn bởi các
đường: (C ), trục tung, y= 4; S2 là diện tích hình phẳng giới hạn bởi các đường: (C ) và
trục hoành, x= 3, x= 4. Tỉ số S1
S2
là
−1 1 2 3 4
4
O
S2
S1
x
y
A
S1
S2
= 1. B S1
S2
= 3
2
. C
S1
S2
= 5
4
D
S1
S2
= 3
4
.
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=
p
1− x2 và trục hoành là
A
pi
4
. B pi. C
pi
2
. D 2pi.
Câu 11. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = p−8x−7 và đường thẳng
y=−2x−1 được biểu diễn dưới dạng a
b
, trong đó a, b là các số tự nhiên và phân số
a
b
tối giản. Giá trị của a+b là
A 5. B 7. C 6. D 8.
Câu 12. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các
đường y= cotx, y= 0, x= pi
4
, x= pi
2
là
A pi
(
1− pi
4
)
. B pi
(
1+ pi
4
)
. C
pi2
4
. D
3pi2
4
.
Câu 13. Diện tích S của hình phẳng giới hạn bởi đường parabol y = x2−3x+2 và hai đường
thẳng y= x−1, x= 0 là
A S = 3
8
. B S = 4
3
. C S = 0. D S = 8
3
.
Câu 14. Cho hai số phức z1 = 3+4i, z2 = a+bi. Môđun của số phức z1 · z2 là
A 5(a2+b2). B 5
p
a2+b2. C 25(a2+b2). D
√
5(a2+b2).
Câu 15. Cho hàm số y = f (x) liên tục trên đoạn [a;b] có đồ thị là (C ). Gọi (H ) là hình phẳng
giới hạn bởi (C ), trục hoành và hai đường thẳng x= a, x= b. Diện tích của (H ) là
A S =
∣∣∣∣∫ b
a
f (x)dx
∣∣∣∣. B S = ∫ b
a
| f (x)|dx. C S =
∫ b
a
f (x)dx. D S =−
∫ b
a
f (x)dx.
Trang 3/4- Mã đề thi 103
Câu 16. Cho số phức z thoả mãn
(z− i)(1+ i)=−2+8i.
Phần ảo của z là
A −4i. B −4. C 3. D 4.
Câu 17. Cho hàm số y= f (x) có đồ thị (C ) như hình vẽ dưới đây. Gọi S là diện tích hình phẳng
giới hạn bởi (C ), hai trục toạ độ và đường thẳng x= 2. Khẳng định nào sau đây đúng?
−1 1 3O
2
2
−2
x
y
A S =
∫ 1
0
f (x)dx−
∫ 2
1
f (x)dx.
B S =
∫ 2
0
f (x)dx.
C S =
∫ 1
0
f (x)dx+
∫ 2
1
f (x)dx.
D S =
∣∣∣∣∫ 2
0
f (x)dx
∣∣∣∣.
Câu 18. Gọi z1, z2 là hai nghiệm phức của phương trình z2−6z+25= 0. Giá trị của
∣∣z31∣∣+ ∣∣z32∣∣ là
A 125. B 50. C 250. D 6750.
Câu 19. Tập hợp các điểm biểu diễn số phức z thoả |z−3+ i| = 2 là
A đường tròn tâm I(3;−1) bán kính bằng 2. B đường tròn tâm I(−3;1) bán kính bằng 2.
C đường tròn tâm I(3;−1) bán kính bằng 4 . D đường tròn tâm I(−3;1) bán kính bằng 4.
Câu 20. Cho số phức z thoả mãn z · (1+2i)= 1−3i. Điểm biểu diễn cho z là
A B(−1;−1) . B C(1;1) . C A(−1;1). D D(1;−1).
—- HẾT—-
Trang 4/4- Mã đề thi 103
Mã đề thi 103 ĐÁP ÁN
Câu 1. A
Câu 2. D
Câu 3. D
Câu 4. B
Câu 5. D
Câu 6. C
Câu 7. D
Câu 8. C
Câu 9. A
Câu 10. C
Câu 11. B
Câu 12. A
Câu 13. D
Câu 14. B
Câu 15. B
Câu 16. B
Câu 17. A
Câu 18. C
Câu 19. A
Câu 20. C
Trang 1/4- Mã đề thi 103