Kiểm tra định kỳ học kỳ I năm học 2014 - 2015 môn: Hình học – Chương I - Lớp 8 - Trường THCS Phan Chu Trinh

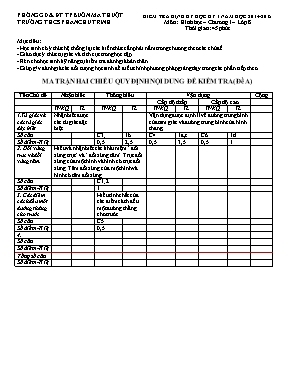
PHÒNG GD & ĐT TP BUÔN MA THUỘT
TRƯỜNG THCS PHAN CHU TRINH
KIỂM TRA ĐỊNH KỲ HỌC KỲ I NĂM HỌC 2014- 2015
Môn: Hình học – Chương I – Lớp 8
Thời gian: 45 phút
Mục tiêu: 
- Học sinh có ý thức hệ thống lại các kiến thức cần phải nắm trong chương theo các chủ đề
- Giáo dục ý thức tự giác và tích cực trong học tập
- Rèn cho học sinh kỹ năng tự kiểm tra đánh giá bản thân
- Giúp g/v đánh giá các đối tượng học sinh để điều chỉnh phương pháp giảng dạy trong các phần tiếp theo
MA TRẬN HAI CHIỀU QUY ĐỊNH NỘI DUNG ĐỀ KIỂM TRA( Đề A)
Tên Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1.Tứ giác và các tứ giác đặc biệt
Nhận biết được các tứ giác đặc biệt
Vận dụng được định lí về đường trung bình của tam giác và đường trung bình của hình thang, 
Số câu
C3;
1b
C4
1a,c
C6
1d
Số điểm-Tỉ lệ
0,5
2,5
0,5
3,5
0,5
1
2. Đối xứng trục và đối xứng tâm. 
Hiểu và nhận biết các khái niệm “đối xứng trục” và “đối xứng tâm” Trục đối xứng của một hình và hình có trục đối xứng. Tâm đối xứng của một hình và hình có tâm đối xứng
Số câu
C1;2
Số điểm-Tỉ lệ
1
3. Các điểm cách đều một đường thẳng cho trước
Hiểu tính chất của các điểm cách đều một đường thẳng cho trước
Số câu
C5
Số điểm-Tỉ lệ
0,5
4.
Số câu
Số điểm-Tỉ lệ
Tổng số câu
Số điểm-Tỉ lệ
PHÒNG GD & ĐT TP BUÔN MA THUỘT
TRƯỜNG THCS PHAN CHU TRINH
KIỂM TRA ĐỊNH KỲ HỌC KỲ I- NĂM HỌC 2014- 2015
Môn: Hình học– Chương I – Lớp 8
Thời gian: 45 phút
ĐỀ A
A/- Trắc nghiệm khách quan: 
 Chọn theo yêu cầu của mỗi câu và ghi chữ cái đầu câu vào giấy bài làm
 Câu 1: Gọi H là trực tâm của tam giác ABC cân tại A, điểm đối xứng của H qua BC là K thì ta suy ra:
A. Tam giác BHK là tam giác đều	B. BHCK là hình vuông
C. BHCK là hình thoi	D. BHCK là hìn chữ nhật
 Câu 2: Trong các hình sau đây, hình nào không có tâm đối xứng
A. Đoạn thẳng AB	B. Tam giác đều ABC
C. Hình bình hành	D. Đường thẳng xy
Câu 3: Cho hình thang ABCD có AB // CD. Biết rằng và . Số đo góc B bằng
A. 	B. 	C.	D. 
Câu 4: Cho tam giác đều ABC có . Gọi D, E lần lượt là trung điểm các cạnh AB và AC. Chu vi tứ giác BDEC bằng 
A. 15cm	B. 9cm	C. 12cm	D. 20cm
 Câu 5: Chọn câu trả lời đúng:
A. Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là một đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h
B. Tập hợp các điểm cách một đường thẳng một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h
C. Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h thay đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h
D. Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h
 Câu 6: Hình thoi ABCD có chu vi bằng 30cm và đường cao BH bằng 3cm thì ta suy ra số đo đúng của các góc A và B là 
A. 	B. 	C. 	D. 
B/- Tự luận Cho hình vuông ABCD, điểm M thuộc đường chéo AC. Vẽ E, F theo thứ tự là các hình chiếu của M trên AD, CD. 
a) MEDF là hình gì? Vì sao?
b) Chứng minh AF = BE
c) Chứng minh BE vuông góc với AF
d) Chứng minh CE = BF
e) Chứng minh ba đường thẳng BM, AF, CE cùng đi qua một điểm
ĐÁP ÁN & HƯỚNG DẪN CHẤM Mã đề A
I*Đáp án:
A / Trắc nghiệm: 6x 0,5 = 3 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
C
B
D
A
D
C
B/ Tự luận (7 điểm)
Bài
Câu
Hướng dẫn giải
Điểm
0,5
a
a) MEDF là hình gì? Vì sao?
ME ^ AD nên ; MF ^ CD nên 
0,5
ABCD là hình vuông nên 
0,5
Vậy MEDF là hình chữ nhật
0,5
b
b) Chứng minh AF = BE
ABCD là hình vuông nên ta có: AB = AD, và AC là tia phân giác góc BAD
0,5
Vậy nên ΔEAD vuông cân đỉnh E nên EM = EA
0,5
Mà MEDF là hình chữ nhật nên EM = DF. Vậy EA = DF
0,5
Từ đó ΔAEB = ΔDFA (c-g-c) suy ra AF = BE
0,5
c
c) Chứng minh BE vuông góc với AF
Ta có (góc tương ứng) mà 
0.75
Nên do đó ΔAPB vuông tại P nên AF vuông góc với BE tại P
0.75
d
d) Chứng minh CE = BF
Hoàn toàn tương tự trên ta có ΔDEC = ΔCFB (c-g-c) nên CE = BF
0,5
e
e) Chứng minh ba đường thẳng BM, AF, CE cùng đi qua một điểm
Hoàn toàn tương tự trên ta có ΔDEC = ΔCFB (c-g-c) và suy ra CE vuông góc với BF tại Q
0,25
Ta có MFCK có và CM là tia phân giác góc KCF nên MFCK là hình vuông
0,25
Suy ra MK = MF=CK = CF và KB = CB – CK= CD – CF = DF = ME
Vậy ΔKBM = ΔMEF (c-g-c) nên tương tự câu c ta có BM vuông góc với EF tại H
0,25
Vậy BM, AF, CE là ba đường cao của ΔBEF nên cùng đi qua một điểm
0,25
PHÒNG GD & ĐT TP BUÔN MA THUỘT
TRƯỜNG THCS PHAN CHU TRINH
KIỂM TRA ĐỊNH KỲ HỌC KỲ I- NĂM HỌC 2014- 2015
Môn: Hình học – Chương I – Lớp 8
Thời gian: 45 phút
ĐỀ B
A/- Trắc nghiệm khách quan 
Chọn theo yêu cầu của mỗi câu và ghi chữ cái đầu câu vào giấy bài làm
Câu 1: Cho hình thang ABCD có AB // CD. Biết rằng và . Số đo góc C bằng
A.	B.	C.	D.
Câu 2: Chọn câu trả lời đúng:
A. Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h thay đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h
B. Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là một đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h
C. Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h
D. Tập hợp các điểm cách một đường thẳng một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h
Câu 3: Trong các hình sau đây, hình nào không có trục đối xứng
A. Hình thoi	B. Tam giác đều ABC
C. Đoạn thẳng AB	D. Đường thẳng xy
Câu 4: Hình thoi ABCD có chu vi bằng 30cm và đường cao BH bằng 3cm thì ta suy ra số đo đúng của các góc A và B là 
A. 	B. 	C. 	D. 
Câu 5: Gọi H là trọng tâm của tam giác ABC cân tại A, điểm đối xứng của H trung điểm BC là K thì ta suy ra:
A. Tam giác BHC là tam giác đều	B. BHCK là hình vuông
C. BHCK là hình chữ nhật	D. 
Câu 6: Cho tam giác đều ABC có . Gọi D, E lần lượt là trung điểm các cạnh AB và AC. Chu vi tứ giác BDEC bằng 
A. 15cm	B. 20cm	C. 9cm	D. 12cm 
B/- Tự luận : Cho hình vuông ABCD, điểm M thuộc đường chéo AC. Vẽ I, K theo thứ tự là các hình chiếu của M trên BA, BC. 
a) MIBK là hình gì? Vì sao?
b) Chứng minh CI = DK
c) Chứng minh CI vuông góc với DK]
d) Chứng minh DI = AK
e) Chứng minh ba đường thẳng DM, CI, AK cùng đi qua một điểm
ĐÁP ÁN & HƯỚNG DẪN CHẤM Mã đề B
I*Đáp án:
A / Trắc nghiệm: 6x 0,5 = 3 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
C
C
D
A
D
B
B/ Tự luận (7 điểm)
Bài
Câu
Hướng dẫn giải
Điểm
0,5
a
a) MIBK là hình gì? Vì sao?
MI ^ AB nên ; MK ^ BC nên 
0,5
ABCD là hình vuông nên 
0,5
Vậy MIBK là hình chữ nhật
0,5
b
b) Chứng minh CI = DK
ABCD là hình vuông nên ta có: CB = CD, và AC là tia phân giác góc BCD
0,5
Vậy nên ΔKCM vuông cân đỉnh K nên KM = KC
0,5
Mà MIBK là hình chữ nhật nên KM = BI. Vậy BI = KC
0,5
Từ đó ΔBIC = ΔCKD (c-g-c) suy ra CI = DK
0,5
c
c) Chứng minh CI vuông góc với DK
Ta có (góc tương ứng) mà 
0.75
Nên do đó ΔHCD vuông tại H nên CI vuông góc với DK tại H
0.75
d
d) Chứng minh DI = AK
Hoàn toàn tương tự trên ta có ΔBKA = ΔAID (c-g-c) nên DI = AK
0,5
e
e) Chứng minh ba đường thẳng DM, CI, AK cùng đi qua một điểm
Hoàn toàn tương tự trên ta có ΔBKA = ΔAID (c-g-c) và suy ra DI vuông góc với AK tại S
0,25
Ta có MEAI có và AM là tia phân giác góc EAI nên MEAI là hình vuông
0,25
Suy ra MI = MF=AI = AE và MK = IB = AB – BI= AD – AE = DE
Vậy ΔMIK = ΔEMD (c-g-c) nên tương tự câu c ta có DM vuông góc với KI tại N
0,25
Vậy DM, CI, AK là ba đường cao của ΔDIK nên cùng đi qua một điểm
0,25
II*Hướng dẫn chấm: 
- Giáo viên có thể chia nhỏ điểm thành phần trong từng câu để chấm
- Điểm toàn bài là tổng điểm thành phần làm tròn theo quy chế
- Học sinh có thể lập luận cách khác nhưng đủ ý và chặt chẽ vẫn cho điểm thành phần tương ứng
- Khi cùng một lỗi về cách viết kí hiệu nếu lập lại chỉ trừ một lần điểm là 0,25 trong toàn bài
- Khi học sinh sai về cách trình bày logic nhưng có hướng chứng minh đúng giáo viên nên xem xét cho điểm kiến thức
PHÒNG GD & ĐT T/P BUÔN- MA- THUỘT
TRƯỜNG THCS PHAN CHU TRINH
KIỂM TRA ĐỊNH KỲ NĂM HỌC 2014- 2015
Môn: Hình học – Lớp 8
Thời gian: 45 phút
MA TRẬN HAI CHIỀU QUY ĐỊNH NỘI DUNG ĐỀ KIỂM TRA
Tên Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1.
Số câu
Số điểm-Tỉ lệ
2.
Số câu
Số điểm-Tỉ lệ
3.
Số câu
Số điểm-Tỉ lệ
4.
Số câu
Số điểm-Tỉ lệ
Tổng số câu
Số điểm-Tỉ lệ
PHÒNG GD & ĐT T/P BUÔN- MA- THUỘT
TRƯỜNG THCS PHAN CHU TRINH
KIỂM TRA ĐỊNH KỲ NĂM HỌC 2014- 2015
Môn: Hình học – Lớp 8
Thời gian: 45 phút
ĐỀ A
A/- Trắc nghiệm khách quan 
 Câu1 : 
	A. 
	B. 
	C. 
	D. 
 Câu 2. 
	A. 
	B. 
	C. 
	D. 
 Câu 3: 
	A.
	B. 
	C. 
	D. 
 Câu 4: 
	A. 
	B. 
	C. 
	D. 
 Câu 5: 
	A. 
	B. 
	C. 
	D. 
 Câu 6: 
	A. 
	B. 
	C. 
	D. 
B/- Tự luận :
Bài 1: 
Bài 2: 
Bài 3: 
ĐÁP ÁN & HƯỚNG DẪN CHẤM Mã đề A
I*Đáp án:
A / Trắc nghiệm: 6x 0,5 = 3 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
B/ Tự luận (7 điểm)
Bài
Câu
Hướng dẫn giải
Điểm
PHÒNG GD & ĐT T/P BUÔN- MA- THUỘT
TRƯỜNG THCS PHAN CHU TRINH
KIỂM TRA ĐỊNH KỲ NĂM HỌC 2014- 2015
Môn: Hình học – Lớp 8
Thời gian: 45 phút
ĐỀ B
A/- Trắc nghiệm khách quan 
 Câu1: 
A. 
B. 
C. 
D. 
Câu2: 
A. 
B. 
C. 
D. 
Câu3: 
A. 
B. 
C. 
D. 
Câu4: 
A. 
B. 
C. 
D. 
Câu5: 
A. 
B. 
C. 
D. 
Câu6: 
A. 
B. 
C. 
D. 
B/- Tự luận :
Bài 1: 
Bài 2: 
Bài 3: 
ĐÁP ÁN & HƯỚNG DẪN CHẤM Mã đề B
I*Đáp án:
A / Trắc nghiệm: 6x 0,5 = 3 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
B/ Tự luận (7 điểm)
Bài
Câu
Hướng dẫn giải
Điểm
II*Hướng dẫn chấm: 
- Giáo viên có thể chia nhỏ điểm thành phần trong từng câu để chấm
- Điểm toàn bài là tổng điểm thành phần làm tròn theo quy chế
- Học sinh có thể lập luận cách khác nhưng đủ ý và chặt chẽ vẫn cho điểm thành phần tương ứng