Kiểm tra chương III Hình học 9 – HK II

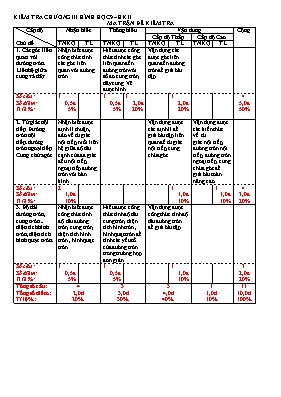
KIỂM TRA CHƯƠNG III HÌNH HỌC 9 –HK II
MA TRẬN ĐỀ KIỂM TRA
Cấp độ
Chủ đề
Nhận biêt
Thông hiểu
Vận dung
Cộng
Cấp độ Thấp
Cấp độ Cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1. Các góc liên quan với đường tròn. Liên hệ giữa cung và dây
Nhận biết được công thức tính các góc liên quan với đường tròn.
Hiểu được công thức tính các góc liên quan đến đường tròn với số đo cung tròn, dây cung. Vẽ được hình
Vận dụng các được góc liên quan đến đường tròn để giải bài tập
Số câu :
Số điểm:
Tỉ lệ %:
1
0,5đ
5%
1
0,5đ
5%
1
2,0đ
20%
1
2,0đ
20%
4
5,0đ
50%
2. Tứ giác nội tiếp. Đường tròn nội tiếp.đường tròn ngoại tiếp. Cung chứa góc
Nhận biết được định lí thuận , đảo về tứ giác nội tiếp, mối liên hệ giữa độ dài cạnh của đa giác đều nội tiếp, ngoại tiếp đường tròn với bán kính. 
Vận dụng được các định lí để giải bài tập liên quan đế tứ giác nội tiếp, cung chứa góc.
Vận dụng được các kiến thức về tứ
giác nội tiếp, đường tròn nội tiếp, đường tròn ngoại tiếp, cung chứa góc để giải bài toán nâng cao.
Số câu :
Số điểm:
Tỉ lệ %:
2
1,0đ
10%
1
1,0đ
10%
1
1,0đ
10%
4
3,0đ
20%
3. Độ dài đường tròn, cung tròn ; diện tích hình tròn, diện tích hình quạt tròn. 
Nhận biết được công thức tính độ dài đường tròn, cung tròn, diện tích hình tròn , hình quạt tròn 
Hiểu được công thức tính độ dài cung tròn, diện tích hình tròn , hình quạt tròn để tính các yếu tố của đường tròn trong trường hợp đơn giản.
Vận dụng được công thức tính độ dài đường tròn để giải bài tập
Số câu :
Số điểm:
Tỉ lệ %:
1
0,5đ
5%
1
0,5đ
5%
1
1,0đ
10%
3
2,0đ
20%
Tổng số câu:
Tổng số điểm:
Tỉ lệ %:
4
2,0đ
20%
3
3,0đ
30%
3
4,0đ
40%
1
1,0đ
10%
11
10,0đ
100%
TRƯỜNG THCS NHƠN PHÚC	NĂM HỌC: 2013-2014
Họ và tên.........................................................Lớp.....................Ngày kiểm tra.......................
	BÀI KIỂM TRA CHƯƠNG III – HÌNH HỌC 9 ( BÀI SỐ 5)
I..TRẮC NGHIỆM. (5 điểm)
Chọn câu trả lời đúng nhất để điền vào bảng sau:
Câu
1
2
3
4
5
6
7
8
9
10
Trả lời
Câu 1: Cho là dây cung của đ/tròn (O;R). Số đo là:
 A. B. C. D. 
Câu 2: Cho tam giác ABC nội tiếp (O), khoảng cách từ O đến cạnh AB, AC, BC là OI, OK, OL. Cho biết OI < OL < OK. Cách sắp xếp nào sau đây đúng:
 A. << B.<< C. << D.<<
Câu 3: trong hình vẽ bên bằng bao nhiêu nếu biết sđ ;sđ?
 A. B. C. D. 
Câu 4: Bán kính hình tròn là bao nhiêu nếu có diện tích là (cm2)
 A. 4 cm B. 6 cm C. 3 cm D. 5 cm
Câu 5: Cho (O;R) và cung AB, sđ.Độ dài cung (tính theo R) là:
 A. ;B. C. D. 
Câu 6: Diện tích hình vành khăn giới hạn hình tròn (O;8cm) và (O;4cm) là:
 A. B. C. D.
Câu 7: Trên đ/tròn (O) lấy theo thứ tự 4 điểm A, B, C, D sao cho sđ, sđ, sđ.
Gọi I là giao điểm của AC và BD. Sđ là:
 A. B. C. D. 
Câu 8: Cho là dây cung của (O;R). M là một điểm trên cung lớn, số đo là:
 A. 300 B. 450 C. 600 D. 1200
Câu 9: Đường tròn nội tiếp lục giác đều cạnh 6 cm có bán kính là:
 A. 6 cm B. 3 cm C. cm D. cm
Câu 10: Diện tích hình tròn là (cm2). Vậy chu vi của hình tròn là:
 A. cm B. cm C. cm D. cm
II.TỰ LUẬN. (5 điểm)
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. Đường thẳng BM cắt đường tròn (O) tại D. Đường thẳng AD cắt đường tròn (O) tại S.
1.Chứng minh ABCD là tứ giác nội tiếp .
2.Gọi E là giao điểm của BC với đường tròn (O). Chứng minh 
3.Chứng minh rằng các đường thẳng BA, EM, CD đồng quy.
4.Chứng minh điểm M là tâm đường tròn nội tiếp tam giác ADE.
	BÀI LÀM
TRƯỜNG THCS NHƠN PHÚC	NĂM HỌC: 2013-2014
Họ và tên.........................................................Lớp.....................Ngày kiểm tra.......................
	BÀI KIỂM TRA CHƯƠNG III – HÌNH HỌC 9 ( BÀI SỐ 5)
I..TRẮC NGHIỆM. (5 điểm)
Chọn câu trả lời đúng nhất để điền vào bảng sau:
Câu
1
2
3
4
5
6
7
8
9
10
Trả lời
Câu 1: Cho là dây cung của đ/tròn (O;R). Số đo là:
 A. B. C. D. 
Câu 2: Từ 8 giờ đến 10 giờ, kim giờ quay được một góc ở tâm là:
 A. 300 B. 600 	 C. 900 	 D. 450 
Câu 3: Cho là góc nội tiếp của đường tròn (O) chắn . Vậy số đo của là:
 A.1300 B. 2600 	 C. 1000 	 D. 650 
Câu 4: Tứ giác ABCD nội tiếp đường tròn (O) khi:
 A. + + + = 3600 	B. + = + = 1800
 C. + = + = 1800	 D. Cả ba kết luận trên đều đúng
Câu 5: Cho hình vuông nội tiếp (O; R). Diện tích của hình vuông bằng:
 A. R2	B. R2	C. 2R2	D. 3R2
Câu 6 : Diện tích hình vành khăn giới hạn bởi hai đường tròn (O;10cm) và (O;6cm) là:
 A. 67(cm2)	B. 64(cm2)	C. 72(cm2)	D. Tất cả đều đúng
Câu 7: Trên đ/tròn (O) lấy theo thứ tự 4 điểm A, B, C, D sao cho sđ, sđ, sđ.Gọi I là giao điểm của AC và BD. Sđ là:
 A. B. C. D. 
Câu 8: Bộ 4 số đo nào sau đây chỉ số đo bốn góc của một tứ giác nội tiếp ?
 A. 500 ; 600 ; 1300 ; 1400 	B. 650 ; 850 ; 950 ; 1150 
 C. 820 ; 900 ; 980 ; 1000 	 D. Các câu trên đều sai
Câu 9: Cho là dây cung của (O;R). M là một điểm trên cung lớn, số đo là:
 A. 300 B. 450 C. 600 D. 1200
Câu 10: Đường tròn nội tiếp lục giác đều cạnh 6 cm có bán kính là:
 A. 6 cm B. 3 cm C. cm D. cm 
II.TỰ LUẬN. (5 điểm)
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. Đường thẳng BM cắt đường tròn (O) tại D. Đường thẳng AD cắt đường tròn (O) tại S.
1.Chứng minh ABCD là tứ giác nội tiếp .
2.Gọi E là giao điểm của BC với đường tròn (O). Chứng minh .
3.Chứng minh rằng các đường thẳng BA, EM, CD đồng quy.
4.Chứng minh điểm M là tâm đường tròn nội tiếp tam giác ADE.
	Bài làm
	HƯỚNG DẪN CHẤM
I..TRẮC NGHIỆM. (5 điểm)Mỗi ý đúng 0,5điểm
Câu
1
2
3
4
5
6
7
8
9
10
Trả lời
Câu
1
2
3
4
5
6
7
8
9
10
Trả lời
II.TỰ LUẬN. (5 điểm)
 Hình vẽ có hai trường hợp: vẽ hình đúng 0,5 điểm
Tia CS nằm giữa hai tia CD và CE
Tia CD nằm giữa hai tia CS và CE
1.Chứng minh ABCD là tứ giác nội tiếp .
Ta có ÐCAB = 900 ( vì tam giác ABC vuông tại A);
 Ð MDC = 900 ( góc nội tiếp chắn nửa đường tròn )
 => ÐCDB = 900 như vậy D và A cùng nhìn BC dưới một góc bằng 900 nên A và D cùng nằm trên đường tròn đường kính BC 
=> ABCD là tứ giác nội tiếp được một đường tròn đường kính BC
2.Chứng minh DM là tia phân giác của góc ADE.
ABCD là tứ giác nội tiếp đường kính BC
 => ÐD1= ÐC3 ( nội tiếp cùng chắn cung AB). 
 ÐD1= ÐC3 => Cung SM = Cung EM 
=> ÐC2 = ÐC3 (hai góc nội tiếp đường tròn (O) chắn hai cung bằng nhau) 
=> CA là tia phân giác của ÐSCB.
 	Theo trên Ta có Cung SM = Cung EM => ÐD1= ÐD2
 	=> DM là tia phân giác của góc ADE (1)
3.Chứng minh rằng các đường thẳng BA, EM, CD đồng quy.
Xét DCMB Ta có BA^CM; CD ^ BM; ME ^ BC 
 Vậy BA, EM, CD là ba đường cao của CMB nên BA, EM, CD đồng quy.
4. Chứng minh điểm M là tâm đường tròn nội tiếp tam giác ADE.
Ta có ÐMEC = 900 (nội tiếp chắn nửa đường tròn (O)) 
 	 => ÐMEB = 900. 
Tứ giác AMEB có ÐMAB = 900 ; ÐMEB = 900 
=> ÐMAB + ÐMEB = 1800 mà đây là hai góc đối nên tứ giác AMEB nội tiếp một đường tròn => ÐA2 = ÐB2 .
Tứ giác ABCD là tứ giác nội tiếp => ÐA1= ÐB2
 ( nội tiếp cùng chắn cung CD) 
=> ÐA1= ÐA2 => AM là tia phân giác của góc DAE (2)
Từ (1) và (2) Ta có M là tâm đường tròn nội tiếp tam giác ADE