Kiểm tra chương I môn Giải tích 12

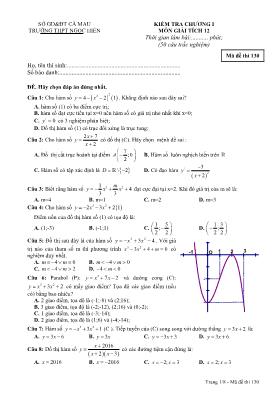
 Trang 1/8 - Mã đề thi 130 
SỞ GD&ĐT CÀ MAU 
TRƯỜNG THPT NGỌC HIỂN 
KIỂM TRA CHƯƠNG I 
MÔN GIẢI TÍCH 12 
Thời gian làm bài:........... phút; 
(50 câu trắc nghiệm) 
 Mã đề thi 130 
Họ, tên thí sinh:.......................................................................... 
Số báo danh:............................................................................... 
ĐỀ. Hãy chọn đáp án đúng nhất. 
Câu 1: Cho hàm số    224 2 1y x   . Khẳng định nào sau đây sai? 
A. hàm số (1) có ba điểm cực trị; 
B. hàm số đạt cực tiểu tại x=0 nên hàm số có giá trị nhỏ nhất khi x=0; 
C. / 0y  có 3 nghiệm phân biệt; 
D. Đồ thị hàm số (1) có trục đối xứng là trục tung; 
Câu 2: Cho hàm số 2 7
2
xy
x



 có đồ thị (C). Hãy chọn mệnh đề sai : 
A. Đồ thị cắt trục hoành tại điểm 7 ;0
2
A  
 
 B. Hàm số luôn nghịch biến trên  
C. Hàm số có tập xác định là  \ 2D   D. Có đạo hàm 
 
/
2
3
2
y
x



Câu 3: Biết rằng hàm số 3 21 4
3 3
my x x    đạt cực đại tại x=2. Khi đó giá trị của m sẽ là: 
A. m=4 B. m=1 C. m=2 D. m=3 
Câu 4: Cho hàm số  3 22 3 2 1y x x    
Điểm uốn của đồ thị hàm số (1) có tọa độ là: 
A. (1;-3) B. (-1;1) C. 1 5;
2 2
  
 
 D. 1 3;
2 2
  
 
Câu 5: Đồ thị sau đây là của hàm số 43 23  xxy . Với giá 
trị nào của tham số m thì phương trình 3 23 4 0x x m    có 
nghiệm duy nhất. 
A. 4 0m m    B. 4 0m m    
C. 4 2m m    D. 4 0m   
Câu 6: Parabol (P): 2 7 2y x x   và đường cong (C): 
3 23 2y x x   có mấy giao điểm? Tọa độ các giao điểm (nếu 
có) bằng bao nhiêu? 
A. 2 giao điểm, tọa độ là (-1;-8) và (2;16); 
B. 3 giao điểm, tọa độ là (-2;-12), (2;16) và (0;-2); 
C. 1 giao điểm, tọa độ là (-3;-14); 
D. 2 giao điểm, tọa độ là (1;6) và (-4;-14); 
Câu 7: Hàm số 3 23 1y x x    (C ). Tiếp tuyến của (C) song song với đường thẳng 3 2y x  là: 
A. 3 6y x  B. 3y x C. 3 3y x   D. 3 6y x  
Câu 8: Đồ thị hàm số 
  
2016
2 3
xy
x x


 
 có các đường tiệm cận đứng là: 
A. 2016x  B. 2016x   C. 2; 3x x   D. 2; 3x x  
-2
-4
1O 3-1 2
 Trang 2/8 - Mã đề thi 130 
Câu 9: Cho hàm số  4 3 24 8 8 1 1y x x x x     
Khẳng định nào sau đây sai? 
A.   / 21 2 2y x x x    
B. / 0y  có nghiệm duy nhất x=1 
C. Hàm số (1) đồng biến trên khoảng (1;+∞) 
D. Nếu a<b<0 thì hàm số (1) nghịch biến trên khoảng (a;b) 
Câu 10: Giá trị lớn nhất của hàm số 
22 3
6 2
x xy
x
 


 trên khoảng (3;8) bằng 
A. 15
2
 B. 25
2
 C. 10
3
 D. 25
3
Câu 11: Đồ thị nào trong các hàm số sau không có tiệm cận? 
A. 24 3y x x   B. 1xy
x

 C. 
2
2
2
1
x xy
x



 D. 1
1
xy
x



Câu 12: Cho hàm số  
23 7 5 1
2
x xy
x
 


Xét hai mệnh đề: 
(I). 
 
2
/ /
2
3 12 9 ; 0 1 3
2
x xy y x x
x
 
     

. Và / 0y  có hai nghiệm phân biệt nên hàm số (1) 
có hai điểm cực trị. 
(II). Hai cực trị của hàm số là    1 1; 3 11y y   . Vì    1 1 3 11y y    nên hàm số (1): 
+ Đạt cực tiểu tại x=1 và 1CTy   ; 
+ Đạt cực đại tại x=3 và 11CDy  
Mệnh đề nào đúng? Mệnh đề nào sai? 
A. (I) đúng và (II) sai; B. (I) và (II) đều đúng; 
C. (I) sai và (II) đúng; D. (I) và (II) đều sai; 
Câu 13: Hàm số 4 21 2 1
4
y x x   có giá trị cực tiểu và giá trị cực đại là: 
A. 2; 0CT CDy y   B. 3; 1CT CDy y   C. 3; 0CT CDy y   D. 2; 0CT CDy y  
Câu 14: Đường thẳng 2y x  và đồ thị hàm số 
22 4
2
x xy
x
 


 có mấy giao điểm? Tọa độ các giao 
điểm (nếu có) bằng bao nhiêu? 
A. 2 giao điểm, tọa độ là (0;-2) và (-1;-3); B. 2 giao điểm, tọa độ là (1;-1) và (2;0); 
C. 1 giao điểm, tọa độ là (3;1); D. Không có giao điểm; 
Câu 15: Giá trị nhỏ nhất của hàm số 5 3y x x    trên đoạn [-5;3] là: 
A. 
 5;3
min 4
x
y
 
 B. 
 5;3
min 5
x
y
 
  C. 
 5;3
min 2 2
x
y
 
 D. 
 5;3
min 3
x
y
 
 
Câu 16: Hàm số 4 21 2
4 2
my x x    có giá trị cực đại 6CDy  . Khi đó, giá trị tham số m là : 
A. m=2 B. m=-2 C. m=-4 D. m=4 
Câu 17: Cho hàm số  3 23 9 5 *y x x x     
Xét hai mệnh đề: 
(1): Hàm số (*) đồng biến trên khoảng (-1;3) 
(2): Nếu (a;b) (0;+∞) thì hàm số (*) nghịch biến trên khoảng (a;b) 
Mệnh đề nào sau đây là đúng? Mệnh đề nào sau đây là sai? 
A. (2) đúng và (1) sai; B. (1) và (2) đều sai; 
C. (1) đúng và (2) sai; D. (1) và (2) đều đúng; 
 Trang 3/8 - Mã đề thi 130 
Câu 18: Với giá trị nào của tham số m thì hàm số 4 21
4
y x mx m   có ba cực trị. 
A. m0 
Câu 19: Hàm số 4 21 2 3
4
y x x    nghịch biến trong khoảng nào sau đây: 
A.  ;0 B.  2; C.  0; D. (0; 2) 
Câu 20: Cho hàm số  
2
/ /
ax bx cy f x
a x b
 
 

 có bảng biến thiên sau: 
Hàm số  y f x là hàm số nào trong bốn hàm số sau: 
A. 42
2
y x
x
  

 B. 
2 8
2
x xy
x
 


 C. 63
2
y x
x
  

 D. 
22
2
x xy
x



Câu 21: Cho hàm số    3 2 0y f x ax bx cx d a      
có bảng biến thiên: 
Hàm số nào trong các hàm số sau có bảng biến thiên như 
trên? 
A.    31 1f x x   B.    31 1f x x   
C.    31 1f x x   D.    31 1f x x   
Câu 22: Cho hàm số  3 22 3 1 1y x x   . Xét hai mệnh đề 
(I): Hàm số (1) đạt cực đại tại x=-1 và yCD=0; 
(II): Điểm cực tiểu của đồ thị hàm số (1) là (0;-1) 
Mệnh đề nào sau đây đúng? Mệnh đề nào sai? 
A. (I) và (II) đều sai; B. (II) đúng và (I) sai; 
C. (I) đúng và (II) sai; D. (I) và (II) đều đúng; 
Câu 23: Cho hàm số  
 
 2
3 1 2
2
1 2
x x
xy f x
x x x
     
    
 . Khẳng định nào sau đây sai? 
A. Khi x=-4 thì / 9y   B. Khi x=0 thì 1
2
y   
C. Đồ thị hàm số không có đường tiệm cận. D. Tập xác định của hàm số là D   
Câu 24: Cho hàm số 3 23 1y x x    . Khoảng đồng biến của hàm số này là: 
A. (0; 2) B.  2; C.  ;0 D.  0; 
Câu 25: Cho hàm số        
3
2 2 22 3 1 1
3
xy f x m m x m x m         
Tính m để hàm số (1) qua một cực đại (hoặc cực tiểu) tại 0 2x   . Sau đây là bài giải. 
Bước 1. Ta có      / 2 2 22 2 3 1f x x m m x m       
Bước 2. Hàm số (1) qua một cực đại (hoặc cực tiểu) tại 0 2x   
 Trang 4/8 - Mã đề thi 130 
     / 2 2
2
2 0 4 4 2 3 1 0
4 3 0 1 3
f m m m
m m m m
          
       
Bước 3. Khi 1 3m m   thì hàm số (1) qua một cực đại (hoặc cực tiểu) tại 0 2x   . 
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu? 
A. Đúng; B. Sai từ bước 1; C. Sai từ bước 3.; D. Sai từ bước 2; 
Câu 26: Giá trị lớn nhất của hàm số 3 23 3 4y x x x    trên đoạn  0;4 lần lượt là: 
A. 
 0;4
max 5
x
y

 B. 
 0;4
max 32
x
y

 C. 
 0;4
max 4
x
y

 D. 
 0;4
max 64
x
y

 
Câu 27: Với giá trị nào của tham số m thì hàm số 4mxy
x m



 đồng biến trên khoảng  1; 
A. m2 C.   m ;m2 2 D.   m ;m1 2 
Câu 28: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
22 2
2
x xy
x
 


 trên đoạn [-2;1] lần lượt bằng: 
A. 2 và 0; B. 1 và (-2); C. 0 và (-2); D. 1 và (-1); 
Câu 29: Giá trị của a là bao nhiêu thì đồ thị hàm số 4 22y x x a    đi qua điểm M(1:1) 
A. a=1 B. a=4 C. a=2 D. a=3 
Câu 30: Đồ thị hàm số 2 1
2
xy
x


 
 có tiệm cận đứng và tiệm cận ngang lần lượt là: 
A. 2; 2x y   B. 2; 2x y   C. 2; 2x y    D. 2; 2x y  
Câu 31: Đồ thị nào trong các hàm số sau có tiệm cận? 
A. 22 3y x x   B. 4 23 2y x x   C. 
23 2
2
x xy
x
 


 D. 23 1y x x   
Câu 32: Cho hàm số 33 23  xxy (1) khẳng định nào sau đây đúng? 
A. Hàm số (1) nghịch biến trên khoảng (0;2) B. Hàm số (1) nghịch biến trên khoảng (-2;0); 
C. Hàm số (1) nghịch biến trên khoảng (-∞;0); D. Hàm số (1) nghịch biến trên khoảng (0;+ ∞) 
Câu 33: Đồ thị hàm số 
2
3 1
x xy
x



 có bao nhiêu đường tiệm cận? 
A. 2 B. 3 
C. 0 D. 1 
Câu 34: Biết đồ thị hàm số 3 23 2y x x   là hình vẽ sau 
Đồ thị của hàm số 3 23 2y x x   là hình vẽ nào trong bốn hình sau: 
A. B. 
C. D. 
 Trang 5/8 - Mã đề thi 130 
Câu 35: Cho hàm số 3 23 2016y x x   có đồ thị (C). Hãy chọn phát biểu sai : 
A. Có tập xác định  \ 2016D   B. Đồ thị hàm số có hai điểm cực trị. 
C. Đồ thị có tâm đối xứng  1;2018I  D. Đồ thị đi qua điểm  1;2020M 
Câu 36: Cho hàm số 4 28 1y x x    và bốn điểm    2 89 2 3 890;1 , ; , ; , 1;8
9 3 93
A B C D
  
       
. 
Điểm nào là điểm uốn của đồ thị hàm số (1)? 
A. A và B; B. B và C; C. C và D; D. D và A 
Câu 37: (Page Design). Một tờ giấy có chiều dài 
 x inch và chiều rộng  y inch trong đó phần in được 
chiếm diện tích  230 inch . Phần lề trên và dưới của tờ 
giấy là  1 inch và phần lề ngang trái phải của tờ giấy là 
 2 inch (Xem hình). 
Khi đó, hàm số để tính tổng diện tích của tờ giấy được 
biểu diễn theo ẩn x sẽ là: 
A.  2 11
4
x x
S
x



 B. S xy C. 
 2 11
4
x x
S
x



 D.  2 11
4
x x
S
x



Câu 38: Cho hàm số      22 3 1f x x x   . Xét ba mệnh đề sau: 
(I). / 20 4 3 0y x x     
(II). Đồ thị hàm số (1) là hình vẽ sau: 
(III). Hàm số (1) đồng biến trên khoảng (1;3) 
Mệnh đề nào đúng? Mệnh đề nào sai? 
A. (2) và (3) đúng, (1) sai; B. (1) và (2) 
đúng, (3) sai; 
C. (3) đúng, (1) và (2) sai; D. (2) sai, (1) và (3) đúng; 
Câu 39: Cho hàm số   ax by f x
cx d

 

 có đồ thị như hình vẽ 
sau: 
Hàm số y=f(x) là hàm số nào trong bốn hàm số sau? 
A. 2 1
2
xy
x



 B. 1 2
2
xy
x



C.  2 1
2
x
y
x



 D. 2 1
2
xy
x



Câu 40: Cho hàm số  4 24 4 1y x x   . Khẳng định nào sau đây 
sai? 
A. Đạo hàm có ba nghiệm, đó là 0; 2x x   
B. Đồ thị có hai điểm uốn là 2 16 2 16; , ;
3 9 3 9
A B
   
      
   
C. Đồ thị có trục đối xứng là trục tung; 
D. Hàm số có giá trị cực đại bằng 4 và giá trị cực tiểu bằng 0; 
 Trang 6/8 - Mã đề thi 130 
Câu 41: Phương trình tiếp tuyến của đồ thị hàm số 2 1
2
xy
x


 
 tại điểm có hoành độ x=1 là: 
A. 5 8y x   B. 5 8y x  C. 5 2y x   D. 5 2y x  
Câu 42: Cho hàm số  2 3 1
2
xy
x



. Khẳng định nào sau đây sai? 
A. 
 
/
2
7
2
y
x


B. Vì / 0y  với mọi x nên hàm số (1) đồng biến trên R; 
C. Bảng biến thiên 
D. Đồ thị hàm số (1) có tâm đối xứng là (-2;2) 
Câu 43: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 23 9 1y x x x    trên đoạn [0;3] lần lượt 
bằng: 
A. 25 và 0; B. 36 và (-5); C. 54 và 1; D. 28 và (-4); 
Câu 44: (HOW DO YOU SEE IT?). The graph of a rational function 
   
 
N x
f x
D x
 is shown below. 
Determine which of the satements about the function is false. 
A. N(0)=2 
B. The ratio of the leading coefficients of N(x) and D(x) is 1; 
C. D(1)=0; 
D. The degrees of N(x) and D(x) are equal; 
Câu 45: Đồ thị hàm số 2
1
xy
x


 cắt đường thẳng 3 2 0x y   tại 
mấy điểm? 
A. 1 B. 2 C. 3 D. 0 
Câu 46: Chứng minh đường thẳng :m y x m    luôn cắt đồ thị (C) của hàm số 
2
1
xy
x



 tại hai 
điểm phân biệt P và Q. Tính m để độ dài PQ ngắn nhất? 
Sau đây là bài giải. 
Bước 1. Phương trình hoành độ giao điểm của m và (C) là: 
 2
12
2 0 *1
xx x m
x mx mx
 
    
    
Bước 2. Ta có 
   
   
2
22
1 1 2 1 0
4 2 2 4 0,
m m
m m m m
      

          
Vậy phương trình (*) luôn có hai nghiệm phân biệt 1 2, 1x x  . 
Suy ra m luôn cắt (C) tại hai điểm phân biệt    1 1 2 2; ; ;P x x m Q x x m    (đpcm) 
Bước 3.      2 2 21 2 2 1 1 22PQ x x x x x x      
 222. 2 3 2. 1 2 2m m m       
Vậy PQ ngắn nhất bằng 2 khi m=1. 
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu? 
 Trang 7/8 - Mã đề thi 130 
A. Đúng; B. Sai từ bước 1; C. Sai từ bước 2; D. Sai từ bước 3; 
Câu 47: Đường thẳng y ax b  cắt đồ thị hàm số 1 2
1 2
xy
x



 tại hai điểm A và B có hoành độ lần 
lượt bằng (-1) và 0. Lúc đó, a và b bằng bao nhiêu? 
A. a=1 và b=2 B. a=4 và b=1; C. a=-2 và b=1; D. a=-3 và b=2 
Câu 48: Cho hàm số  4 22 3 1y x x    . Hàm số (1) có bảng biến thiên là bảng nào sau đây? 
A. 
B. 
C. 
D. 
Câu 49: Giao điểm của đồ thị (C) 3 1
1
xy
x



 và đường thẳng (d): 3 1y x  là: 
A. Điểm   12;5 , ;0
3
M N   
 
 B. (d) và (C) không có điểm chung. 
C. Điểm  1 ;0 , 0; 1
3
M N   
 
 D. Điểm  2;5M 
Câu 50: Tìm giá trị nhỏ nhất của hàm số 2 1y x
x
  trên khoảng (0;1)? 
A. 3 2
2
 B. 2 3
3
 C. 
33 2
2
 D. 
32 3
3
----------------------------------------------- 
----------- HẾT ---------- 
 Trang 8/8 - Mã đề thi 130 
ĐÁP ÁN 
mamon made cauhoi dapan 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 1 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 2 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 3 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 4 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 5 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 6 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 7 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 8 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 9 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 10 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 11 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 12 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 13 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 14 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 15 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 16 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 17 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 18 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 19 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 20 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 21 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 22 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 23 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 24 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 25 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 26 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 27 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 28 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 29 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 30 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 31 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 32 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 33 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 34 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 35 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 36 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 37 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 38 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 39 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 40 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 41 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 42 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 43 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 44 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 45 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 46 D 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 47 B 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 48 C 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 49 A 
2016_HK1_GT12_KT45P_1(15-10-2016) 130 50 C