Kiểm tra 45 phút lần 1 HK II môn: Toán khối: 11

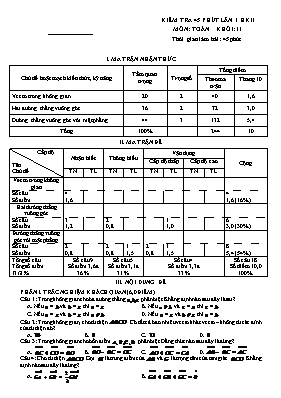
	KIỂM TRA 45 PHÚT LẦN 1 HKII
	MÔN: TOÁN KHỐI: 11
	Thời gian làm bài: 45 phút
I. MA TRẬN NHẬN THỨC
Chủ đề hoặc mạch kiến thức, kỹ năng
Tầm quan trọng
Trọng số
Tổng điểm
Theo ma trận
Thang 10
Vectơ trong không gian
20
2
40
1,6
Hai đường thẳng vuông góc
36
2
72
3,0
Đường thẳng vuông góc với mặt phẳng
44
3
132
5,4
Tổng
100%
244
10
II. MA TRẬN ĐỀ
 Cấp độ
Tên 
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
TN
TL
TN
TL
TN
TL
TN
TL
Vectơ trong không gian
Số câu
Số điểm
4
1,6
4
1,6 (16%)
Hai đường thẳng vuông góc
Số câu
Số điểm
3
1,2
2
0,8
1
1,0
6
3,0 (30%) 
Đường thẳng vuông góc với mặt phẳng
Số câu
Số điểm
2
0,8
2
0,8
1
1,5
2
0,8
1
1,5
8
5,4 (54%)
Tổng số câu 
Tổng số điểm
Tỉ lệ %
Số câu 9
Số điểm 3,6đ
36 %
Số câu 5
Số điểm 3,1đ
31 %
Số câu 4
Số điểm 3,3đ
33 %
Số câu 18
Số điểm 10,0
100%
III. NỘI DUNG ĐỀ
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (6,0 ĐIỂM)
Câu 1: Trong không gian cho ba đường thẳng phân biệt. Khẳng định nào sau đây là sai?
A. Nếu và thì .	B. Nếu và thì .
C. Nếu và thì .	D. Nếu và thì .
Câu 2: Trong không gian, cho tứ diện . Có tất cả bao nhiêu vectơ khác vectơ – không từ các đỉnh của tứ diện đó?
A. .	B. .	C. .	D. .
Câu 3: Trong không gian cho bốn điểm phân biệt. Đẳng thức nào sau đây là đúng?
A. .	B. .	C. .	D. .
Câu 4: Cho tứ diện . Gọi là trung điểm của và là trọng tâm của tam giác . Khẳng định nào sau đây là đúng?
A. .	B. .
C. .	D. .
Câu 5: Trong không gian, cho hình hộp . Mệnh đề nào sau đây là đúng?
A. .	B. .
C. .	D. .
Câu 6: Trong không gian, cho hai đường thẳng và vuông góc với nhau. Phát biểu nào sau đây là đúng?
A. Chúng chéo nhau.	B. Chúng có cùng vectơ chỉ phương.
C. Chúng cắt nhau.	D. Góc giữa chúng bằng .
Câu 7: Cho hình chóp có đáy là hình vuông và vuông góc với mặt đáy. Mệnh đề nào sau đây là đúng?
A. .	B. .	C. .	D. .
Câu 8: Trong không gian, cho hình chóp có đáy là hình chữ nhật và vuông góc với mặt phẳng . Hình chiếu vuông góc của xuống mặt phẳng là đường thẳng nào sau đây?
A. .	B. .	C. .	D. .
Câu 9: Trong không gian, cho hình chóp có đáy là hình bình hành và vuông góc với mặt phẳng . Hình chiếu vuông góc của xuống mặt phẳng là đường thẳng nào sau đây?
A. .	B. .	C. .	D. .
Câu 10: Cho hình chóp có đáy là hình vuông và vuông góc với mặt phẳng . Mặt phẳng nào vuông góc với đường thẳng ?
A. .	B. .	C. .	D. .
Câu 11: Cho tứ diện đều cạnh . Tính số đo góc giữa hai đường thẳng và .
A. .	B. .	C. .	D. .
Câu 12: Cho hình chóp có đáy là hình vuông tâm và vuông góc với đáy . Xác định góc giữa và mặt phẳng là góc nào sau đây?
A. .	B. .	C. .	D. .
Câu 13: Cho hình chóp có đáy là tam giác vuông tại , , và . Gọi là trung điểm của . Gọi là góc giữa và mặt phẳng . Số đo góc bằng bao nhiêu độ?
A. .	B. .	C. .	D. .
Câu 14: Cho hình chóp có vuông góc với đáy , biết và . Tính số đo góc giữa hai đường thẳng và .
A. .	B. .	C. .	D. .
Câu 15: Cho hình chóp có đáy là hình thoi và . Góc giữa đường thẳng và mặt phẳng là góc nào sau đây?
A. .	B. .	C. .	D. .
PHẦN II. TỰ LUẬN (4,0 ĐIỂM)
Cho hình chóp có đáy là hình vuông cạnh , vuông góc với mặt đáy và 
1/ Chứng minh rằng vuông góc với ; vuông góc với .
2/ Tính góc giữa và mặt phẳng .
3/ Trên hai cạnh và lần lượt lấy hai điểm và sao cho . Chứng minh rằng vuông góc với .
IV. HƯỚNG DẪN CHẤM
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
Mã đề 132
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
A
C
A
D
C
D
B
B
A
B
A
D
C
D
C
Mã đề 209
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
C
D
B
C
C
B
A
A
B
D
C
A
A
B
D
Mã đề 357
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
C
B
B
C
A
A
D
A
A
B
C
D
C
D
B
Mã đề 485
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
C
C
A
B
D
C
A
A
D
C
D
B
A
B
B
PHẦN II. TỰ LUẬN
CÂU
ĐÁP ÁN
ĐIỂM
1
(1,5 điểm)
Chứng minh rằng vuông góc với ; vuông góc với .
Xét và có:
 (vì là hình vuông)
0,25
 (vì )
0,25
Vậy .
0,25
Xét và có:
 (vì là hình vuông)
0,25
 (vì )
0,25
Vậy .
0,25
2
(1,5 điểm)
Tính góc giữa và mặt phẳng .
Vì .
 tại .
0,25
Nên là hình chiếu vuông góc của xuống .
0,25
Vậy góc giữa và là góc giữa và bằng .
0,25
Ta có .
Trong tam giác vuông :
0,5
Cho nên .
0,25
3
(1,0 điểm)
Trên hai cạnh và lần lượt lấy hai điểm và sao cho . Chứng minh rằng vuông góc với .
Xét và có:
 (hai đường chéo của hình vuông )
 (vì )
Vậy .
0,5
Nên .
0,25
Cho nên suy ra .
0,25