Kiểm tra 1 tiết Đại số 8 - Trường THCS Võ Thị Sáu

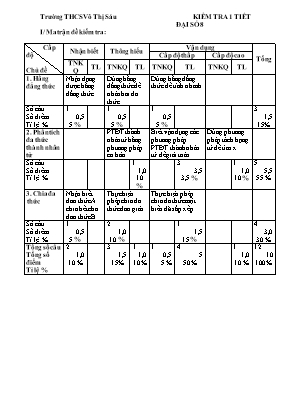
Trường THCS Võ Thị Sáu 	KIỂM TRA 1 TIẾT
	ĐẠI SỐ 8	
I/ Ma trận đề kiểm tra:
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1. Hằng đẳng thức
Nhận dạng được hằng đẳng thức
Dùng hằng đẳng thức để nhân hai đa thức
Dùng hằng đẳng thức để tính nhanh
Số câu 
Số điểm 
Tỉ lệ %
1
0,5
5 %
1
0,5
5 %
1
0,5
5 %
3
1,5
15%
2. Phân tích đa thức thành nhân tử
PTĐT thành nhân tử bằng phương pháp cơ bản
Biết vận dụng các phương pháp PTĐT thành nhân tử để giải toán
Dùng phương pháp tách hạng tử để tìm x
Số câu 
Số điểm 
Tỉ lệ %
1
1,0
10 %
3
3,5
3,5 %
1
1,0
10 %
5
5,5 
55 %
3. Chia đa thức
Nhận biết đơn thức A chia hết cho đơn thức B
Thực hiện phép chia đa thức đơn giản
Thực hiện phép chia đa thức một biến đã sắp xếp
Số câu 
Số điểm 
Tỉ lệ %
1
0,5
5 %
2
1,0
10 %
1
1,5
15 %
4
3,0
30 %
Tổng số câu
Tổng số điểm
Tỉ lệ %
2 
1,0
10 %
3
1,5
15%
 1
1,0
10 % 
1
0,5
5 %
4
5
50 %
1
1,0
10 %
12
10
100 %
Đề:KIỂM TRA THỬ CHƯƠNG I DẠI 8
I. TRẮC NGHIỆM: Đánh dấu X vào ô vuông của câu trả lời đúng trong các câu sau:
1) Đơn thức – 12x2yz2t4 chia hết cho đơn thức nào sau đây:
A. c –2x2y3zt3	B. c 5x2yz2t	C. c 2x2yz3t2	D. c –x2y3z3t4
2) ( 4x – 2 ) ( 4x + 2 ) = 
A. c 4x2 + 4x+4	B. c 4x2 – 4 	C. c 16x2 + 4	 D. c 16x2 – 4
3) Giá trị của ( –8x2y3 ) : ( –3xy2 ) tại x = –2 ; y = –3 là:
A. c 16	B. c –	C. c -16	D. c 
4) Kết quả của phép tính là: ( x )5 : ( – x )2
A. c – x3	B. c x3	C. c – x4	D. c x4
5) Biểu thức thích hợp của đẳng thức 81x2 +  + 25y2 = ( 9x + 5y )2 là: 
A. c 45xy	B. c – 45xy C. c 90xy	D. c – 90xy 
6) Đa thức x2 - 4xy + 4y2 được phân tích thành nhân tử là:
A. c (x + 2y)2 	B.c (2x – y )2 C. c (x – 2y)2 D. c –(2x + y)2
7) Với ( x – 1 )2 = x – 1 thì giá trị của x sẽ là:
A. c 0 	B. c – 1 	C. c 1 hoặc 2 	D. c 0 hoặc 1
8) Biểu thức thích hợp của đẳng thức 27x3 + y3 = ( 3x + y )( ) là : 
A. c 9x2 + 2xy + y2 	B. c 9x2 +3 xy + y2 
C. c 9x2 – 3xy + y2	D. c 9x2 – 6xy + y2
II. TỰ LUẬN: 
Bài 1: Phân tích các đa thức sau thành nhân tử :
a) x2 – y2 – 2x – 2y 	c) 2x2 – 5x – 7
18 m2 – 36 mn + 18 n2 – 72 p2 	d) (x- 1)( x - 2) (x- 3)( x - 4) - 24 
Bài 2: Rút gọn biểu thức : 
A = x ( x + y )2 - x ( x - y )2 ;B = (2x- 3)( 4x2 + 6x + 9) - (2x + 3)( 4x2 - 6x + 9)
C = (x + 3)3 - (x - 3)3 - 18x2 – 18
Làm tính chia : ( x3 + 4x2 – x – 4 ) : ( x + 1 )
Bài 3: Tìm x , biết : 
x ( 3x + 2 ) + ( x + 1 )2 – ( 2x – 5 )( 2x + 5 ) = – 12 
x3 – 5x = 0 	c)( 3x – 4 )2 – ( x + 1 )2
Bài 4: Tìm n Z để 2n2 + 5n – 1 chia hết cho 2n - 1 
Bài 5: Tìm giá trị nhỏ nhất, giá trị lớn nhất ( nếu có) của các biểu thức sau:
A = x2 + 4x + 9 	b) B = ( x+ 1 )( x – 6 ) – 10
c) E = – x2 +2x - 7 	d) K = ( x+ 1 )( 4 – x ) +12
III/ ĐÁP ÁN
Đáp án 2: ĐẠI SỐ 8.
I. TRẮC NGHIỆM: (4 điểm) Mỗi câu đúng được 0,5 điểm. 
1. B	, 2. D	, 3. A 	, 4. A	, 5. C	,6. C	, 7. C	, 8. C
II. TỰ LUẬN: (6 điểm)
Bài 1: (2điểm) Mỗi câu đúng cho 1 điểm.
a/ Biến đổi được: ( x – y )( x + y ) – 2( x + y ) 	(0,5điểm)
	= ( x – y – 2 )( x + y )	(0,5điểm)
b/ Biến đổi được: 18( m2 – 2mn + n2 – 4p2 )	(0,5điểm)
= 18[( m – n )2 – (2p)2 ]= 18( m – n – 2p )( m – n + 2p )	(0,5điểm)
Bài 2: (2điểm)
 a/ Biến đổi được: 	x2( x + y ) + y2 ( x + y ) + 2xy ( x + y )	(0,5điểm)
	= ( x + y )( x2 + y2 + 2xy ) = ( x + y )3	(0,5điểm)
b/ Tính được: 	( x3 + 4x2 – x – 4 ) : ( x + 1 ) = x2 + 3x – 4	(1điểm)
Bài 3: (1điểm)
Biến đổi được: 	 3x2 + 2x + x2 + 2x + 1 – 4x2 + 25 = –12	(0,25điểm)
 	 4x + 26 = –12	 	(0,25điểm)
x = –	(1điểm)
Bài 4: (1điểm)
Tính được: 	( 2n2 + 5n – 1 ) : ( 2n – 1 ) = n + 3 + 	(0,5điểm)
	Để ( 2n2 + 5n – 1 ) ( 2n – 1 ) và n Z ( 2n – 1 ) Ư(2) = 
	 x 	(0,5điểm)
-------------------------------------------------------------------------------------------------------------------
--------------------------