Hóa học - Chuyên đề Phương pháp luyện tập thể tích khối đa diện

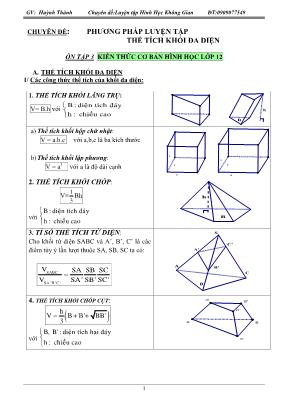
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
1 
B
h
a
b
c
a
a
a
B
h
CHUYÊN ĐỀ: PHƢƠNG PHÁP LUYỆN TẬP 
 THỂ TÍCH KHỐI ĐA DIỆN 
ƠN TẬP 3 KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 12 
A. THỂ TÍCH KHỐI ĐA DIỆN 
I/ Các cơng thức thể tích của khối đa diện: 
1. THỂ TÍCH KHỐI LĂNG TRỤ: 
 V= B.h với 
B: diện tích đáy
h : chiều cao



a) Thể tích khối hộp chữ nhật: 
 V = a.b.c với a,b,c là ba kích thước 
b) Thể tích khối lập phương: 
 V = a
3 
 với a là độ dài cạnh 
2. THỂ TÍCH KHỐI CHĨP: 
 V=
1
3
Bh 
với 
B : diện tích đáy
h : chiều cao



3. TỈ SỐ THỂ TÍCH TỨ DIỆN: 
Cho khối tứ diện SABC và A’, B’, C’ là các 
điểm tùy ý lần lượt thuộc SA, SB, SC ta cĩ: 
SABC
SA 'B'C'
V SA SB SC
V SA' SB' SC'
 
C'
B'
A'
C
B
A
S
4. THỂ TÍCH KHỐI CHĨP CỤT: 
  hV B B' BB'
3
   
với 
B, B' : diện tích hai đáy
h : chiều cao



BA
C
A'
B'
C'
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
2 
a
3a
C'
B'
A'
C
B
A
LOẠI 1: THỂ TÍCH LĂNG TRỤ 
1) Dạng 1: Khối lăng trụ đứng cĩ chiều cao hay cạnh đáy 
Ví dụ 1: Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác ABC vuơng cân tại A 
cĩ cạnh BC = a 2 và biết A'B = 3a. Tính thể tích khối lăng trụ. 
 a 2 
Lời giải: 
 Ta cĩ 
 ABC vuơng cân tại A nên AB = AC = a 
ABC A'B'C' là lăng trụ đứng AA' AB  
2 2 2 2
AA'B AA' A'B AB 8a    
AA' 2a 2  
Vậy V = B.h = SABC .AA' = 
3
a 2 
Ví dụ 2: Cho lăng trụ tứ giác đều ABCD.A’B’C’D' cĩ cạnh bên bằng 4a và đường 
chéo 5a. Tính thể tích khối lăng trụ này. 
5a
4a
D'
C'
B'
A'
D C
BA
Lời giải: 
 ABCD A'B'C'D' là lăng trụ đứng nên 
 BD
2
 = BD'
2
 - DD'
2
 = 9a
2
 BD 3a  
 ABCD là hình vuơng 
3a
AB
2
  
Suy ra B = SABCD = 
2
9a
4
 Vậy V = B.h = SABCD.AA' = 9a
3
 Ví dụ 3: Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh 
 a = 4 và biết diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ. 
A' C'
B'
A
B
C
I
Lời giải: 
 Gọi I là trung điểm BC .Ta cĩ 
ABC đều nên 
AB 3
3 &
2
AI 2 AI BC
A'I BC(dl3 )
 
  
A'BC
A'BC
2S1
S BC.A'I A'I 4
2 BC
    
AA' (ABC) AA' AI   . 
2 2A'AI AA' A'I AI 2    
 Vậy : VABC.A’B’C’ = SABC .AA'= 8 3 
 Ví dụ 4: Một tấm bìa hình vuơng cĩ cạnh 44 cm, người ta cắt bỏ đi ở mỗi gĩc 
 tấm bìa một hình vuơng cạnh 12 cm rồi gấp lại thành một cái hộp chữ nhật 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
3 
A'
D
B'
C'
A'
C
D'
C'
B'B
D'
A
60
D' C'
B'
A'
D C
BA
o60
C'
B'
A'
C
B
A
 khơng cĩ nắp. Tính thể tích cái hộp này. 
D'
A'
C'
B'
D
A
C
B
Giải 
 Theo đề bài, ta cĩ 
AA' = BB' = CC' = DD' = 12 cm 
nên ABCD là hình vuơng cĩ 
AB = 44 cm - 24 cm = 20 cm 
 và chiều cao hộp h = 12 cm 
 Vậy thể tích hộp là 
V = SABCD.h = 4800cm
3
 Ví dụ 5: Cho hình hộp đứng cĩ đáy là hình thoi cạnh a và cĩ gĩc nhọn bằng 
 60
0
 Đường chéo lớn của đáy bằng đường chéo nhỏ của lăng trụ. 
 Tính thể tích hình hộp . 
 Lời giải: 
Ta cĩ tam giác ABD đều nên : BD = a 
và SABCD = 2SABD = 
2a 3
2
Theo đề bài BD' = AC = 
a 3
2 a 3
2
 
2 2DD'B DD' BD' BD a 2    
 Vậy V = SABCD.DD' = 
3a 6
2
2)Dạng 2: Lăng trụ đứng cĩ gĩc giữa đường thẳng và mặt phẳng. 
 Ví dụ 1: Cho lăng trụ đứng tam giác ABC A'B'C' cĩ đáy ABC là tam giác 
 vuơng cân tại B với BA = BC = a ,biết A'B hợp với đáy ABC một gĩc 600 . 
 Tính thể tích lăng trụ. 
 Lời giải: 
 Ta cĩ A'A (ABC) A'A AB&AB   là 
hình chiếu của A'B trên đáy ABC . 
 Vậy ogĩc[A'B,(ABC)] ABA' 60  
0ABA' AA' AB.tan60 a 3   
 SABC = 
21 a
BA.BC
2 2
 
 Vậy V = SABC.AA' = 
3a 3
2
 Ví dụ 2: Cho lăng trụ đứng tam giác ABC A'B'C' cĩ đáy ABC là tam giác 
 vuơng tại A với AC = a , ACB= 60 o biết BC' hợp với (AA'C'C) một gĩc 300. 
 Tính AC' và thể tích lăng trụ. 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
4 
a
o
60
o
30
C'
B'
A'
C
B
A
Lời giải: o a 3ABC AB AC.tan60   . 
Ta cĩ: 
AB AC;AB AA' AB (AA'C'C)    
nên AC' là hình chiếu của BC' trên (AA'C'C). 
Vậy gĩc[BC';(AA"C"C)] = BC'A = 30o 
o
AB
AC'B AC' 3a
tan30
   
 V =B.h = SABC.AA' 
2 2
AA'C' AA' AC' A'C' 2a 2    
ABC là nửa tam giác đều nên 
2
ABC
a 3
S
2
 
 Vậy V = 3a 6 
 Ví dụ 3: Cho lăng trụ đứng ABCD A'B'C'D' cĩ đáy ABCD là hình vuơng cạnh a 
 và đường chéo BD' của lăng trụ hợp với đáy ABCD một gĩc 300. 
 Tính thể tích và tổng diên tích của các mặt bên của lăng trụ . 
o
30
a
D'
C'
A'
B'
D
C B
A
 Giải: 
 Ta cĩ ABCD A'B'C'D' là lăng trụ đứng nên ta 
cĩ: DD' (ABCD) DD' BD   và BD là hình 
chiếu của BD' trên ABCD . 
 Vậy gĩc [BD';(ABCD)] = 0DBD' 30 
0 a 6BDD' DD' BD.tan30
3
   
Vậy V = SABCD.DD' = 
3a 6
3
S = 4SADD'A' = 
24a 6
3
 Ví dụ 4: Cho hình hộp đứng ABCD A'B'C'D' cĩ đáy ABCD là hình thoi cạnh 
 a và BAD = 60
o
 biết AB' hợp với đáy (ABCD) một gĩc 30o . 
 Tính thể tích của hình hộp. 
a
o
30
o
60
D'
C'B'
A'
D
CB
A
 Giải 
ABDđều cạnh a 
2
ABD
a 3
S
4
  
2
ABCD ABD
a 3
S 2S
2
   
ABB'vuơng tạiB oBB' ABtan30 a 3   
 Vậy 
3
ABCD
3a
V B.h S .BB'
2
   
 3) Dạng 3: Lăng trụ đứng cĩ gĩc giữa 2 mặt phẳng 
 Ví dụ 1: Cho lăng trụ đứng tam giác ABC A'B'C' cĩ đáy ABC là tam giác 
 vuơng cân tại B với BA = BC = a ,biết (A'BC) hợp với đáy (ABC) một gĩc 
 60
0
 .Tính thể tích lăng trụ. 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
5 
C'
B'
A'
C
B
A
o
60
Lời giải: 
Ta cĩ A'A (ABC)&BC AB BC A'B    
 Vậy ogĩc[(A'BC),(ABC)] ABA' 60  
0ABA' AA' AB.tan60 a 3   
 SABC = 
21 a
BA.BC
2 2
 
 Vậy V = SABC.AA' = 
3a 3
2
 Ví dụ 2: Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều . Mặt 
 (A’BC) tạo với đáy một gĩc 300 và diện tích tam giác A’BC bằng 8. 
 Tính thể tích khối lăng trụ. 
x
o30
I
C'
B'
A'
C
B
A
Giải: ABC đều AI BC  mà AA' (ABC) 
nên A'I BC (đl 3 ). 
 Vậy gĩc[(A'BC);)ABC)] = A'IA = 30o 
 Giả sử BI = x 3
2
32
x
x
AI  .Ta cĩ 
x
xAI
AIIAAIA 2
3
32
3
2
30cos:':' 0  
 A’A = AI.tan 300 = xx 
3
3
.3 
 Vậy VABC.A’B’C’ = CI.AI.A’A = x
3
 3 
Mà SA’BC = BI.A’I = x.2x = 8 2 x 
 Do đĩ VABC.A’B’C’ = 8 3 
 Ví dụ 3: Cho lăng trụ tứ giác đều ABCD A'B'C'D' cĩ cạnh đáy a và mặt phẳng 
 (BDC') hợp với đáy (ABCD) một gĩc 60o.Tính thể tích khối hộp chữ nhật. 
a
060
O
A'
D'
B'
C'
C
A
D
B
Gọi O là tâm của ABCD . Ta cĩ 
ABCD là hình vuơng nênOC BD 
CC' (ABCD) nên OC'BD (đl 3 ). Vậy 
gĩc[(BDC');(ABCD)] = COC' = 60
o
 Ta cĩ V = B.h = SABCD.CC' 
ABCD là hình vuơng nên SABCD = a
2
OCC' vuơng nên CC' = OC.tan60
o 
=
a 6
2
 Vậy V = 
3
a 6
2
 Ví dụ 4: Cho hình hộp chữ nhật ABCD A'B'C'D' cĩ AA' = 2a ; mặt phẳng 
 (A'BC) hợp với đáy (ABCD) một gĩc 60o và A'C hợp với đáy (ABCD) một 
 gĩc 30
o
 .Tính thể tích khối hộp chữ nhật. 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
6 
2a
o
30
o
60
D'
C'B'
A'
D
C
B
A
Ta cĩ AA' (ABCD) AC là hình chiếu 
của A'C trên (ABCD) . 
Vậy gĩc[A'C,(ABCD)] = oA'CA 30 
BC AB BC A'B (đl 3 ) . 
Vậy gĩc[(A'BC),(ABCD)] = oA'BA 60 
A'ACAC = AA'.cot30o = 2a 3 
A'ABAB = AA'.cot60o = 
2a 3
3
2 2 4a 6ABC BC AC AB
3
    
 Vậy V = AB.BC.AA' = 
316a 2
3
4) Dạng 4: Khối lăng trụ xiên 
 Ví dụ 1: Cho lăng trụ xiên tam giác ABC A'B'C' cĩ đáy ABC là tam giác 
 đều cạnh a , biết cạnh bên là a 3 và hợp với đáy ABC một gĩc 60o . 
 Tính thể tích lăng trụ. 
H
o
60
a
B'
A'
C'
C
B
A
Lời giải: 
 Ta cĩ C'H (ABC) CH  là hình chiếu 
của CC' trên (ABC) 
 Vậy ogĩc[CC',(ABC)] C'CH 60  
0 3aCHC' C'H CC'.sin60
2
   
 SABC = 
2 3a
4
 .Vậy V = SABC.C'H = 
33a 3
8
 Ví dụ 2: Cho lăng trụ xiên tam giác ABC A'B'C' cĩ đáy ABC là tam giác 
 đều cạnh a . Hình chiếu của A' xuống (ABC) là tâm O đường trịn ngoại tiếp 
 tam giác ABC biết AA' hợp với đáy ABC một gĩc 60 . 
 1) Chứng minh rằng BB'C'C là hình chữ nhật. 
 2) Tính thể tích lăng trụ . 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
7 
H
O
o60
C'
A
a
B'
A'
C
B
Lời giải: 
 1) Ta cĩ A'O (ABC) OA  là hình 
chiếu của AA' trên (ABC) 
 Vậy ogĩc[AA',(ABC)] OAA' 60  
 Ta cĩ BB'CC' là hình bình hành ( vì mặt 
bên của lăng trụ) 
 AO BC tại trung điểm H của BC nên 
BC A'H (đl 3  ) 
BC (AA'H) BC AA'    mà AA'//BB' 
nên BC BB' .Vậy BB'CC' là hình chữ nhật. 
2) ABC đều nên 
2 2 a 3 a 3
AO AH
3 3 2 3
   
oAOA' A'O AOtan60 a   
 Vậy V = SABC.A'O = 
3a 3
4
 Ví dụ 3: Cho hình hộp ABCD.A’B’C’D’ cĩ đáy là hình chữ nhật với 
 AB = 3 AD = 7 .Hai mặt bên (ABB’A’) và (ADD’A’) lần lượt tạo với đáy 
 những gĩc 450 và 600. . Tính thể tích khối hộp nếu biết cạnh bên bằng 1. 
H
N
M
D'
C'
B'
A'
D
C
B
A
Lời giải: 
Kẻ A’H )(ABCD ,HM ADHNAB  , 
ADNAABMA  ',' (đl 3 ) 
o o
A'MH 45 ,A'NH 60   
Đặt A’H = x . Khi đĩ 
A’N = x : sin 600 = 
3
2x
AN = HM
x
NAAA 


3
43
''
2
22
Mà HM = x.cot 45
0
 = x 
Nghĩa là x = 
7
3
3
43 2


x
x
Vậy VABCD.A’B’C’D’ = AB.AD.x 
 = 
3
3. 7. 3
7
 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
8 
LOẠI 2: THỂ TÍCH KHỐI CHĨP 
1) Dạng 1: Khối chĩp cĩ cạnh bên vuơng gĩc với đáy 
 Ví dụ 1: Cho hình chĩp SABC cĩ SB = SC = BC = CA = a . Hai mặt (ABC) 
 và (ASC) cùng vuơng gĩc với (SBC). Tính thể tích hình chĩp . 
_
\
/
/
a
B
S
C
A
Lời giải: 
 Ta cĩ 
(ABC) (SBC)
(ASC) (SBC)





AC (SBC)  
Do đĩ 
2 3
SBC
1 1 a 3 a 3
V S .AC a
3 3 4 12
   
 Ví dụ 2: Cho hình chĩp SABC cĩ đáy ABC là tam giác vuơng cân tại B với 
 AC = a biết SA vuơng gĩc với đáy ABC và SB hợp với đáy một gĩc 60o. 
 1) Chứng minh các mặt bên là tam giác vuơng . 
 2)Tính thể tích hình chĩp . 
a
o60
S
C
B
A
Lời giải: 
1) SA (ABC) SA AB&SA AC    
 mà BC AB BC SB   ( đl 3  ). 
Vậy các mặt bên chĩp là tam giác vuơng. 
 2) Ta cĩSA (ABC) AB  là hình chiếu 
của SB trên (ABC). 
 Vậy gĩc[SB,(ABC)] = oSAB 60 . 
ABCvuơng cân nên BA = BC = 
a
2
 SABC = 
2
1 a
BA.BC
2 4
 
o a 6
SAB SA AB.tan60
2
   
Vậy 
2 3
ABC
1 1 a a 6 a 6
V S .SA
3 3 4 2 24
   
 Ví dụ 3: Cho hình chĩp SABC cĩ đáy ABC là tam giác đều cạnh a biết SA 
 vuơng gĩc với đáy ABC và (SBC) hợp với đáy (ABC) một gĩc 60o. 
 Tính thể tích hình chĩp . 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
9 
a
o60
M
C
B
A
S
Lời giải: Mlà trung điểm của BC,vì tam giác 
ABC đều nên AM BCSABC (đl3 ) . 
 Vậy gĩc[(SBC);(ABC)] = oSMA 60 . 
Ta cĩ V = 
ABC
1 1
B.h S .SA
3 3
 
o 3a
SAM SA AMtan60
2
   
Vậy V = 
3
ABC
1 1 a 3
B.h S .SA
3 3 8
  
 Ví dụ 4: Cho hình chĩp SABCD cĩ đáy ABCD là hình vuơng cĩ cạnh a và SA 
 vuơng gĩc đáy ABCD và mặt bên (SCD) hợp với đáy một gĩc 60o. 
 1) Tính thể tích hình chĩp SABCD. 
 2) Tính khoảng cách từ A đến mặt phẳng (SCD). 
H
a
D
C
B
A
S
o
60
Lời giải: 1)Ta cĩ SA (ABC) và 
CD AD CD SD   ( đl 3  ).(1) 
 Vậy gĩc[(SCD),(ABCD)] = SDA = 60o . 
SADvuơng nên SA = AD.tan60
o
 = a 3 
Vậy 2
3
ABCD
a
1 1 a 3
V S .SA a 3
3 3 3
   
 2) Ta dựng AH SD ,vì CD (SAD) (do (1) ) 
nên CD AH AH (SCD) 
 Vậy AH là khoảng cách từ A đến (SCD). 
2 2 2 2 2 2
1 1 1 1 1 4
SAD
AH SA AD 3a a 3a
      
 Vậy AH = 
a 3
2
2) Dạng 2 : Khối chĩp cĩ một mặt bên vuơng gĩc với đáy 
Ví dụ 1: Cho hình chĩp S.ABCD cĩ đáy ABCD là hình vuơng cĩ cạnh a 
 Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuơng gĩc với đáyABCD, 
 1) Chứng minh rằng chân đường cao khối chĩp trùng với trung điểm cạnh AB. 
2) Tính thể tích khối chĩp SABCD. 
a
H
D
C
B
A
S
Lời giải: 
1) Gọi H là trung điểm của AB. 
SAB đều SH AB  
mà (SAB) (ABCD) SH (ABCD)   
Vậy H là chân đường cao của khối chĩp. 
2) Ta cĩ tam giác SAB đều nên SA =
a 3
2
suy ra 
3
ABCD
1 a 3
V S .SH
3 6
  
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
10 
Ví dụ 2: Cho tứ diện ABCD cĩ ABC là tam giác đều ,BCD là tam giác vuơng cân tại 
D , (ABC) (BCD) và AD hợp với (BCD) một gĩc 60o . 
Tính thể tích tứ diện ABCD. 
o
60
a
H D
C
B
A
Lời giải: 
 Gọi H là trung điểm của BC. 
Ta cĩ tam giác ABC đều nên AH (BCD) , 
mà (ABC)  (BCD)  AH (BCD) . 
 Ta cĩ AHHDAH = AD.tan60
o 
=a 3 
& HD = AD.cot60
o
 =
a 3
3
BCDBC = 2HD = 
2a 3
3
suy ra 
 V = 
3
BCD
1 1 1 a 3
S .AH . BC.HD.AH
3 3 2 9
  
 Ví dụ 3: Cho hình chĩp S.ABC cĩ đáy ABC là tam giác vuơng cân tại B, cĩ 
 BC = a. Mặt bên SAC vuơng gĩc với đáy, các mặt bên cịn lại đều tạo với mặt đáy một 
gĩc 45
0
. 
a) Chứng minh rằng chân đường cao khối chĩp trùng với trung điểm cạnh AC. 
b) Tính thể tích khối chĩp SABC. 
45
I
J
H
A
C
B
S
Lời giải: 
 a) Kẽ SH BC vì mp(SAC)mp(ABC) nên 
SHmp(ABC). 
 Gọi I, J là hình chiếu của H trên AB và BC  
SIAB, SJBC, theo giả thiết oSIH SJH 45  
 Ta cĩ: HJHISHJSHI  nên BH là 
đường phân giác của ABCừ đĩ suy ra H là trung 
điểm của AC. 
b) HI = HJ = SH =
2
a
VSABC=
12
.
3
1 3a
SHS ABC  
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
11 
3) Dạng 3 : Khối chĩp đều 
Ví dụ 1: Cho chĩp tam giác đều SABC cạnh đáy bằng a và cạnh bên bằng 2a. 
 Chứng minh rằng chân đường cao kẻ từ S của hình chĩp là tâm của tam giác 
đều ABC.Tính thể tích chĩp đều SABC . 
a
2a
H
O
C
B
A
S
Lời giải: 
 Dựng SO (ABC) Ta cĩ SA = SB = SC 
suy ra OA = OB = OC 
 Vậy O là tâm của tam giác đều ABC. 
Ta cĩ tam giác ABC đều nên 
 AO = 
2 2 a 3 a 3
AH
3 3 2 3
  
2
2 2 2 11a
SAO SO SA OA
3
    
a 11
SO
3
  .Vậy 
3
ABC
1 a 11
V S .SO
3 12
  
Ví dụ 2:Cho khối chĩp tứ giác SABCD cĩ tất cả các cạnh cĩ độ dài bằng a . 
 1) Chứng minh rằng SABCD là chĩp tứ giác đều. 
 2) Tính thể tích khối chĩp SABCD. 
a
O
D
C
B
A
S
Lời giải: 
 Dựng SO  (ABCD) 
 Ta cĩ SA = SB = SC = SD nên 
OA = OB = OC = ODABCD là 
hình thoi cĩ đường trịn gnoại tiếp 
nên ABCD là hình vuơng . 
 Ta cĩ SA
2
 + SB
2
 = AB
2
 +BC
2
 = AC
2
nên ASC vuơng tại S 
2
2
a
OS  
 
3
21 1 2 2.
3 3 2 6
ABCD
a a
V S SO a   
 Vậy 
3
a 2
V
6
 
Ví dụ 3: Cho khối tứ diện đều ABCD cạnh bằng a, M là trung điểm DC. 
a) Tính thể tích khối tứ diện đều ABCD. 
b)Tính khoảng cách từ M đến mp(ABC).Suy ra thể tích hình chĩp MABC. 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
12 
aI
H
O
M
C
B
A
D
Lời giải: 
a) Gọi O là tâm của ABC ( )DO ABC  
1
.
3
ABCV S DO 
2 3
4
ABC
a
S  , 
2 3
3 3
a
OC CI  
2 2ơ ĩ :DOC vu ng c DO DC OC  
6
3
a
 
2 31 3 6 2
.
3 4 3 12
a a a
V   
b) Kẻ MH// DO, khoảng cách từ M đến 
mp(ABC) là MH 
1 6
2 6
a
MH DO  
2 31 1 3 6 2
. .
3 3 4 6 24
MABC ABC
a a a
V S MH    
 Vậy 
3
a 2
V
24
 
Bài tập tƣơng tự: 
Bài 1: Cho hình chĩp đều SABC cĩ cạnh bên bằng a hợp với đáy ABC một gĩc 60o . 
Tính thể tích hình chĩp. Đs: 
3
3a
V
16
 
Bài 2: Cho hình chĩp tam giác đều SABC cĩ cạnh bên a, gĩc ở đáy của mặt bên 
 là 45
o
. 
 1) Tính độ dài chiều cao SH của chĩp SABC . Đs: SH = 
a
3
 2) Tính thể tích hình chĩp SABC. Đs: 
3
a
V
6
 
Bài 3: Cho hình chĩp tam giác đều SABC cĩ cạnh đáy a và mặt bên hợp với đáy 
 một gĩc 60o. Tính thể tích hình chĩp SABC. Đs: 
3
a 3
V
24
 
Bài 4 : Cho chĩp tam giác đều cĩ đường cao h hợp với một mặt bên một gĩc 30o . 
 Tính thể tích hình chĩp. Đs: 
3
h 3
V
3
 
Bài 5 : Cho hình chĩp tam giác đều cĩ đường cao h và mặt bên cĩ gĩc ở đỉnh 
 bằng 60o. Tính thể tích hình chĩp. Đs: 
3
h 3
V
8
 
Bài 6 : Cho hình chĩp tứ giác đều SABCD cĩ cạnh đáy a và oASB 60 . 
 1) Tính tổng diện tích các mặt bên của hình chĩp đều. Đs: 
2
a 3
S
3
 
 2) Tính thể tích hình chĩp. Đs: 
3
a 2
V
6
 
Bài 7 : Cho hình chĩp tứ giác đều SABCD cĩ chiều cao h ,gĩc ở đỉnh của mặt bên 
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
13 
 bằng 60o. Tính thể tích hình chĩp. Đs: 
3
2h
V
3
 
Bài 8: Cho hình chĩp tứ giác đều cĩ mặt bên hợp với đáy một gĩc 45o và khoảng 
 cách từ chân đường cao của chĩp đến mặt bên bằng a. 
 Tính thể tích hình chĩp . Đs: 
3
8a 3
V
3
 
Bài 9: Cho hình chĩp tứ giác đều cĩ cạnh bên bằng a hợp với đáy một gĩc 60o. 
Tính thề tích hình chĩp. Đs: 
3
a 3
V
12
 
Bài 10: Cho hình chĩp SABCD cĩ tất cả các cạnh bằng nhau. Chứng minh rằng 
 SABCD là chĩp tứ giác đều.Tính cạnh của hình chĩp này khi thể tích của 
 nĩ bằng 
3
9a 2
V
2
 . Đs: AB = 3a 
4) Dạng 4 : Khối chĩp & phương pháp tỷ số thể tích 
Ví dụ 1: Cho hình chĩp S.ABC cĩ tam giác ABC vuơng cân ở B, 2AC a , 
 SA vuơng gĩc với đáy ABC , SA a 
 1) Tính thể tích của khối chĩp S.ABC. 
 2) Gọi G là trọng tâm tam giác ABC, mặt phẳng ( ) qua AG và song song 
 với BC cắt SC, SB lần lượt tại M, N. Tính thể tích của khối chĩp S.AMN 
G
M
N
I
C
B
A
S
Lời giải: 
a)Ta cĩ: .
1
.
3
S ABC ABCV S SA và SA a 
 + â ĩ : 2ABCc n c AC a AB a    
21
2
ABCS a  Vậy: 
3
21 1. .
3 2 6
SABC
a
V a a  
b) Gọi I là trung điểm BC. 
 G là trọng tâm,ta cĩ : 
2
3
SG
SI
 
  // BC  MN// BC 
2
3
SM SN SG
SB SC SI
    
4
.
9
SAMN
SABC
V SM SN
V SB SC
   
 Vậy: 
34 2
9 27
SAMN SABC
a
V V  
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
14 
Ví dụ 2: Cho tam giác ABC vuơng cân ở A và AB a . Trên đường thẳng qua C và 
vuơng gĩc với mặt phẳng (ABC) lấy điểm D sao cho CD a . Mặt phẳng qua C vuơng 
gĩc với BD, cắt BD tại F và cắt AD tại E. 
a) Tính thể tích khối tứ diện ABCD. 
b) Chứng minh ( )CE ABD 
c) Tính thể tích khối tứ diện CDEF. 
a
a
F
E
B
A
C
D
Lời giải: 
a)Tính ABCDV : 
3
ABCD ABC
1 a
V S .CD
3 6
  
b)Tacĩ: 
,AB AC AB CD  ( )AB ACD  AB EC  
 Ta cĩ: DB EC ( )EC ABD  
c) Tính EFDCV :Ta cĩ: . (*)
DCEF
DABC
V DE DF
V DA DB
 
 Mà 2.DE DA DC , chia cho 2DA 
2 2
2 2
1
2 2
DE DC a
DA DA a
    
 Tương tự: 
2 2
2 2 2
1
3
DF DC a
DB DB DC CB
  

 Từ(*) 
1
6
DCEF
DABC
V
V
  .Vậy
31
6 36
DCEF ABCD
a
V V  
Ví dụ 3: Cho khối chĩp tứ giác đều SABCD. Một mặt phẳng )( qua A, B và trung điểm 
M của SC . Tính tỉ số thể tích của hai phần khối chĩp bị phân chia bởi mặt phẳng đĩ. 
N
S
O
M
B
D
C
A
Lời giải: 
 Kẻ MN // CD (N )SD thì hình thang ABMN là 
thiết diện của khối chĩp khi cắt bởi mặt phẳng 
(ABM). 
 + SABCDSADBSANB
SADB
SAND VVV
SD
SN
V
V
4
1
2
1
2
1
 
SABCDSBCDSBMN
SBCD
SBMN VVV
SD
SN
SC
SM
V
V
8
1
4
1
4
1
2
1
.
2
1
.  
Mà VSABMN = VSANB + VSBMN = SABCDV
8
3
. 
Suy ra VABMN.ABCD = SABCDV
8
5
 Do đĩ : 
5
3
.

ABCDABMN
SABMN
V
V
GV: Huỳnh Thành Chuyên đề:Luyện tập Hình Học Khơng Gian ĐT:0909077549 
15 
I
O
A
B C
D
S
E
F
M
Ví dụ 4: Cho hình chĩp tứ giác đều S.ABCD, đáy là hình vuơng cạnh a, cạnh bên tạo với 
đáy gĩc 60

. Gọi M là trung điểm SC. Mặt phẳng đi qua AM và song song với BD, cắt 
SB tại E và cắt SD tại F. 
a) Hảy xác định mp(AEMF) 
b) Tính thể tích khối chĩp S.ABCD 
c) Tính thể tích khối chĩp S.AEMF 
d) 
Lời giải: 
a) Gọi I SO AM  . Ta cĩ (AEMF) //BD 
EF // BD 
b) . D D
1
.
3
S ABC ABCV S SO với 
2
DABCS a 
 + SOA cĩ : 
6
.tan 60
2
a
SO AO   
 Vậy : 
3
. D
6
6
S ABC
a
V  
c) Phân chia chĩp tứ giác ta cĩ 
. EMFS AV = VSAMF + VSAME =2VSAMF 
 .S ABCDV = 2VSACD = 2 VSABC 
Xét khối chĩp S.AMF và S.ACD 
 Ta cĩ : 
1
2
SM
SC
  
 SAC cĩ trọng tâm I, EF // BD nên: 
2
3
SI SF
SO SD
  
D
1
.
3
SAMF
SAC
V SM SF
V SC SD
   
3
D D
1 1 6
3 6 36
SAMF SAC SAC
a
V V V    
3 3
. EMF
6 6
2
36 18
S A
a a
V   
Ví dụ 5: Cho hình chĩp S.ABCD cĩ đáy ABCD là hình vuơng cạnh a, SA vuơng gĩc 
đáy, 2SA a . Gọi B’, D’ là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng (AB’D’) 
cắt SC tại C’. 
a) Tính thể tích khố