Giáo án Kiểm tra 45 phút môn: Hình học lớp 9

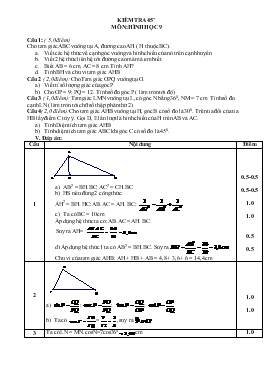
KIỂM TRA 45’
MÔN: HÌNH HỌC 9
Câu 1: ( 5,0 điểm)
Cho tam giác ABC vuông tại A, đường cao AH ( H thuộc BC).
Viết các hệ thức về cạnh góc vuông và hình chiếu của nó trên cạnh huyền
Viết 2 hệ thức liên hệ tới đường cao mà mà em biết.
Biết AB = 6 cm, AC = 8 cm. Tính AH?
Tính BH và chu vi tam giác AHB
Câu 2 ( 2,0 điểm): Cho Tam giác OPQ vuông tại O.
Viết tỉ số lượng giác của góc P
Cho OP = 9; PQ = 12. Tính số đo góc P ( làm tròn tới độ)
Câu 3 ( 1,0 điểm): Tam giác LMN vuông tại L, có góc N bằng 360, NM = 7 cm. Tính số đo cạnh LN ( làm tròn tới chữ số thập phân thứ 2)
Câu 4( 2,0 điểm): Cho tam giác AHB vuông tại H, góc B có số đo là 300. Trên tia đối của tia HB lấy điểm C tùy ý. Gọi D, E lần lượt là hình chiếu của H trên AB và AC.
Tính Diện tích tam giác AHB
Tính diện tích tam giác ABC khi góc C có số đo là 450.
V. Đáp án:
Câu
Nội dung
Điểm
1
AB2 = BH.BC; AC2 = CH. BC
HS nêu đúng 2 công thức:
AH2 = BH. HC; AB.AC = AH. BC; 
Ta có BC = 10cm
Áp dụng hệ thức ta có: AB.AC = AH. BC.
 Suy ra AH= 
d) Áp dụng hệ thức 1 ta có AB2 = BH. BC. Suy ra 
Chu vi của tam giác AHB: AH + HB + AB = 4,8 + 3,6 + 6 = 14,4 cm
0.5-0.5
0.5-0.5
1.0
1.0
0.5
0.5
2
a) ; ; ; 
b) Ta có =, suy ra 
1.0
1.0
3
Ta có LN = MN.cosN=7cos360 cm
1.0
4
Diện tích tam giác AHB
Ta có AH = AB.sinB= 10sin300 = 5 cm ; HB = AB.cosB= 10cos300=cm
SAHB = 1/2AH.HB = ½.5. cm2
D tam giác AHC vuông tại H và góc C bằng 450 nên tam giác AHC vuông cân tại H, suy ra HC = HA = 5 cm.
Diện tích tam giác AHC: SAHC = 1/2AH.CH= ½.5.5 = 12,5 cm2
Vậy SABC = SAHC + S AHB = 34,15 cm2
0.5
0.5
0.25
0.5
0.25
Thường Phước 2, ngày 18 tháng 10 năm 2015
Duyệt của BGH	Duyệt của tổ	GVBM