Đề và đáp án kiểm tra Toán 12 - Trường THPT A Nghĩa Hưng

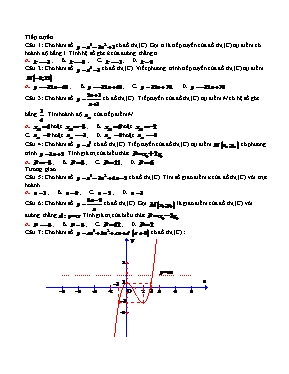
Tiếp tuyến
Câu 1: Cho hàm số có đồ thị (C). Gọi ∆ là tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 1. Tính hệ số góc k của đường thẳng ∆.
A. ; B. ; C. ; D. .
Câu 2: Cho hàm số có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm .
A. ; B. ; C. ; D. .
Câu 3: Cho hàm số có đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm M có hệ số góc bằng . Tìm hoành độ của tiếp điểm M.
A. hoặc ; B. hoặc ; 
C. hoặc ; D. hoặc .
Câu 4: Cho hàm số có đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm có phương trình . Tính giá trị của biểu thức .
A. ; B. ; C. ; D. .
Tương giao
Câu 5: Cho hàm số có đồ thị (C). Tìm số giao điểm n của đồ thị (C) với trục hoành.
A. ; B. ; C. ; D. .
Câu 6: Cho hàm số có đồ thị (C). Gọi là giao điểm của đồ thị (C) với đường thẳng . Tính giá trị của biểu thức .
A. ; B. ; C. ; D. .
Câu 7: Cho hàm số có đồ thị (C) : 
Tìm tất cả các giá trị của tham số m sao cho đường thẳng cắt đồ thị (C) tại ba điểm phân biệt.
A. ; B. ; C. ; D. .
Câu 8: Cho hàm số có đồ thị (C). Tìm tất cả các giá trị của tham số m để đường thẳng cắt đồ thị (C) tại đúng hai điểm phân biệt.
A. ; B. ; C. ; D. .
Tiệm cận
Câu 9: Cho hàm số có và . Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị hàm số đã cho có một tiệm cận ngang là đường thẳng ;
B. Đồ thị hàm số đã cho có hai tiệm cận ngang ;
C. Đồ thị hàm số đã cho có một tiệm cận ngang là đường thẳng ;
D. Đồ thị hàm số đã cho không có tiệm cận ngang.
Câu 10: Cho hàm số có đồ thị (C). Khẳng định nào sau đây là khẳng định đúng ?
A. Nếu thì đường thẳng là tiệm cận đứng của đồ thị (C) ;
B. Nếu thì đường thẳng là tiệm cận đứng của đồ thị (C) ;
C. Nếu thì đường thẳng là tiệm cận đứng của đồ thị (C);
D. Nếu thì đường thẳng là tiệm cận đứng của đồ thị (C).
Câu 11: Các đường tiệm cận của đồ thị hàm số là
A. và ; B. và ; 
C. và ; D. và .
Câu 12: Cho (C1) là đồ thị của hàm số và (C2) là đồ thị của hàm số . Tổng số tất cả các đường tiệm cận của hai đồ thị đã cho bằng
A. 2 ; B. 1 ; C. 4 ; D. 3.
Câu 13: Cho hàm số ( m là tham số ) có đồ thị (C). Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị (C) có đúng hai tiệm cận là các đường thẳng và ;
B. Đồ thị (C) có đúng ba tiệm cận là các đường thẳng , và ;
C. Đồ thị (C) có đúng hai tiệm cận là các đường thẳng và ;
D. Đồ thị (C) có đúng hai tiệm cận là các đường thẳng và .
Câu 14: Tìm tất cả các giá trị của tham số m sao cho đồ thị của hàm số có đúng hai đường tiệm cận.
A. ; B. ; C. ; D. .
Cực trị
Câu 15: Cho hàm số xác định, liên tục trên R và có bảng biến thiên
x
y’
y
Khẳng định nào sau đây là khẳng định sai ?
A. Hàm số đạt cực tiểu tại ;
B. Hàm số có hai điểm cực trị ;
C. Hàm số có giá trị cực đại bằng 2 ;
D. Hàm số đạt cực đại tại .
Câu 16: Cho hàm số có đạo hàm cấp hai trên R. Khẳng định nào sau đây là khẳng định đúng ?
A. Nếu thì là điểm cực tiểu của hàm số ;
B. Nếu thì là điểm cực đại của hàm số ;
C. Nếu thì là điểm cực trị của hàm số ;
D. Nếu thì là điểm cực trị của hàm số.
Câu 17: Cho hàm số có đồ thị (C). 
Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị (C) có một điểm cực đại và hai điểm cực tiểu ;
B. Đồ thị (C) có ba điểm cực tiểu ;
C. Đồ thị (C) có hai điểm cực đại và một điểm cực tiểu ;
D. Đồ thị (C) có ba điểm cực đại.
Câu 18: Tìm điểm cực tiểu của hàm số .
A. ; B. ; C. ; D. .
Câu 19: Tìm giá trị cực tiểu của hàm số .
A. ; B. ; C. ; D. .
Câu 20: Tìm tất cả các giá trị của tham số m đề đồ thị của hàm số có hai điểm cực trị A, B sao cho đường thẳng AB song song với đường thẳng .
A. ; B. ; C. ; D. .
Câu 21: Tìm tất cả các giá trị của tham số m đề đồ thị của hàm số có ba điểm cực trị tạo thành một tam giác có diện tích bằng 32.
A. ; B. ; C. ; D. .
Câu 22: Tìm tất cả các giá trị của tham số m đề đồ thị của hàm số có hai điểm cực trị A, B sao cho .
A. ; B. ; C. ; D. .
Giá trị lớn nhất, giá trị nhỏ nhất
Câu 23: Tìm giá trị nhỏ nhất của hàm số trên đoạn .
A. ; B. ; C. ; D. .
Câu 24: Tìm giá trị lớn nhất M của hàm số .
A. ; B. ; C. ; D. .
Câu 25: Tìm giá trị lớn nhất của hàm số trên khoảng .
A. ; B. ; C. ; D. .
Câu 26: Một chất điểm chuyển động theo quy luật . Tính thời điểm t (giây) tại đó gia tốc a (m/s2) của chuyển động đạt giá trị nhỏ nhất.
A. ; B. ; C. ; D. .
Câu 27: Tìm tất cả các giá trị của tham số m để giá trị lớn nhất của hàm số trên đoạn lớn hơn hoặc bằng 2.
A. ; B. ; C. ; D. .
Tính đơn điệu
Câu 28: Cho hàm số có đạo hàm trên khoảng . Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số đồng biến trên khoảng nếu với mọi cặp thuộc khoảng mà nhỏ hơn thì nhỏ hơn ;
B. Hàm số nghịch biến trên khoảng nếu với mọi cặp thuộc khoảng mà nhỏ hơn thì lớn hơn ;
C. Nếu hàm số đồng biến trên khoảng thì với mọi ;
D. Nếu với mọi thì hàm số đồng biến trên khoảng .
Câu 29: Cho hàm số xác định, liên tục trên R và có bảng biến thiên
X
y’
Y
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số đồng biến trên khoảng ;
B. Hàm số nghịch biến trên các khoảng và ;
C. Hàm số nghịch biến trên ;
D. Hàm số đồng biến trên khoảng .
Câu 30: Hỏi hàm số nghịch biến trên khoảng nào ?
A. ; B. ; B. ; B. .
Câu 31: Tìm các khoảng đơn điệu của hàm số . 
A. Hàm số đồng biến trên các khoảng và ;
B. Hàm số nghịch biến trên các khoảng và ;
C. Hàm số nghịch biến trên ;
D. Hàm số đồng biến trên .
Câu 32: Tìm các khoảng đơn điệu của hàm số .
A. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng ;
B. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng ;
C. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng ;
D. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng .
Câu 33: Tìm các khoảng đơn điệu của hàm số .
A. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng ;
B. Hàm số nghịch biến trên khoảng và đồng biến trên khoảng ;
C. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng ;
D. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
Câu 34: Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên R.
A. ; B. ; C. ; D. . 
Câu 35: Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên R.
A. ; B. ; C. ; D. .
Hình học
Câu 36: Khẳng định nào sau đây là khẳng định sai ?
A. Có sáu loại khối đa diện đều ;
B. Khối hộp là khối đa diện lồi ; 
C. Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó ;
D. Khối tứ diện là khối đa diện lồi.
Câu 37: Khẳng định nào sau đây là khẳng định đúng ?
A. Thể tích của một khối hộp chữ nhật bằng tích ba kích thước của nó ;
B. Thể tích khối chóp có diện tích đáy B và chiều cao h là ;
C. Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là ;
D. Thể tích của khối lập phương có cạnh bằng a là a2.
Câu 38: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, ; cạnh bên SA vuông góc với mặt phẳng đáy và . Tính thể tích V của khối chóp S.ABC.
A. ; B. ; C. ; D. .
Câu 39: Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với , biết thể tích của khối hộp ABCD.A’B’C’D’ bằng . Tính chiều cao h của khối hộp ABCD.A’B’C’D’.
A. ; B. ; C. ; D. .
Câu 40: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có . Tính thể tích V của khối lăng trụ ABC.A’B’C’.
A. ; B. ; C. ; D. .
Câu 41: Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy AB và CD với ; cạnh bên SA vuông góc với mặt phẳng đáy và . Tính chiều cao h của hình thang ABCD, biết khối chóp S.ABCD có thể tích bằng .
A. ; B. ; C. ; D. .
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Tam giác SAB vuông tại S, , và mặt bên (SAB) vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp S.ABCD.
A. ; B. ; C. ; D. .
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Tam giác SAB vuông tại S, , và mặt bên (SAB) vuông góc với mặt phẳng đáy. Gọi H là hình chiếu vuông góc của S trên AB và M là điểm thuộc cạnh SC sao cho . Tính thể tích V của khối tứ diện HMCD.
A. ; B. ; C. ; D. .
Câu 44: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Tam giác SAB vuông tại S, , và mặt bên (SAB) vuông góc với mặt phẳng đáy. Gọi M, N tương ứng là điểm thuộc cạnh SC, SD sao cho .Tính thể tích V của khối đa diện SAHMN.
A. ; B. ; C. ; D. .
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và . Tính góc giữa đường thẳng SB và mặt phẳng (ABCD). 
A. ; B. ; C. ; D. .
Câu 46: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và . Tính côsin góc giữa đường thẳng SC và mặt phẳng (SAB).
A. ; B. ; C. ; D. .
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và . Tính góc giữa đường thẳng BD và mặt phẳng SC.
A. ; B. ; C. ; D. .
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và . Tính khoảng cách từ A đến mặt phẳng (SBC).
A. ; B. ; 
C. ; D. .
Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và . Tính khoảng cách h giữa hai đường thẳng chéo nhau AB và SC.
A. ; B. ; C. ; D. .
Câu 50: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và . Gọi M là điểm thuộc cạnh AB sao cho . Tính khoảng cách h giữa hai đường thẳng chéo nhau CM và SD.
A. ; B. ; C. ; D. .