Đề trắc nghiệm Giải tích 12 chương II - Mã đề thi 130

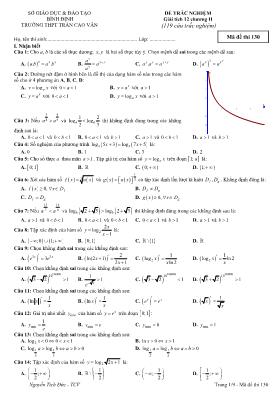
Nguyễn Tích Đức - TCV Trang 1/9 - Mã đề thi 130 
SỞ GIÁO DỤC & ĐÀO TẠO 
 BÌNH ĐỊNH 
TRƯỜNG THPT TRẦN CAO VÂN 
ĐỀ TRẮC NGHIỆM 
Giải tích 12 chương II 
 (119 câu trắc nghiệm) 
Họ, tên thí sinh:..................................................................... Lớp: .................... Mã đề thi 130 
I. Nhận biết 
Câu 1: Cho a, b là các số thực dương; ,x y là hai số thực tùy ý. Chọn mệnh đề sai trong các mệnh đề sau: 
A.  . .x x xa b a b B. 
x
x y
y
a a
a
 C. .x y x ya a a  D.  y yx xa a 
Câu 2: Đường nét đậm ở hình bên là đồ thị của dạng hàm số nào trong các hàm 
số cho ở 4 phương án A, B, C, D: 
A. logay x với 0 1a  B. 
xy a với 1a  
C. xy a với 0 1a  D. logay x với 1a  
Câu 3: Nếu 
43
54a a và 1 2log log
2 3b b
 thì khẳng định đúng trong các khẳng 
định sau là: 
1 2 3
-2
-1
1
2
3
x
y
A. 0 1a  và 0 1b  B. 0 1a  và 1b  C. 1a  và 0 1b  D. 1a  và 1b  
Câu 4: Số nghiệm của phương trình    3 3log 5 3 log 7 5x x   là: 
A. 0 B. 1 C. 3 D. 2 
Câu 5: Cho số thực a thỏa mãn 1a  . Tập giá trị của hàm số logay x trên đoạn  1; a là: 
A.  0; 1 B.  C.  0;  D.  1; 
Câu 6: Xét các hàm số    3f x u x và    
1
3g x u x    có tập xác định lần lượt kí hiệu ,f gD D . Khẳng định đúng là: 
A.   0, ff x x D   B. f gD D 
C. f gD D D.   0, gg x x D   
Câu 7: Nếu 
13 15
7 8a a và    log 2 5 log 2 3b b   thì khẳng định đúng trong các khẳng định sau là: 
A. 1a  và 0 1b  B. 0 1a  và 0 1b  C. 0 1a  và 1b  D. 1a  và 1b  
Câu 8: Tập xác định của hàm số 2
2log
1
xy
x


 là: 
A.    ;0 1;   B.  0; 1 C.  \ 1 D.  
Câu 9: Chọn khẳng định sai trong các khẳng định sau: 
A.  3 33x xe e  B.   2ln(2 1) 2 1x x
 

 C.  2
1log
ln 2
x
x
  D.  2
1log ln 2x
x
  
Câu 10: Chọn khẳng định sai trong các khẳng định sau: 
A.  
1000010
3 2 1  B. 
2
1 1
e
 C.  
1000010
3 2 1  D.  
1000010
3 2 1  
Câu 11: Chọn khẳng định sai trong các khẳng định sau: 
A.   1ln x
x
  B.   1ln x
x
  C.  x xe e  D.   1x
x

 
Câu 12: Giá trị nhỏ nhất miny của hàm số 
xy e trên đoạn  0; 1 : 
A. min
1y
e
 B. miny e C. min 0y  D. min 1y  
Câu 13: Chọn khẳng định sai trong các khẳng định sau: 
A. 2log 0 0 1x x    B. ln 0 1x x   
C. 1 1
3 3
log log 0a b a b    D. 1 1
2 2
log log 0a b a b    
Câu 14: Tập xác định của hàm số 2log 2 1y x  là: 
A. 1 ;
2
   
 
 B. 1\
2
  
 
 C. 1;
2
   
 
 D. 1 ;
2
    
Nguyễn Tích Đức - TCV Trang 2/9 - Mã đề thi 130 
Câu 15: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 1
2
logy x trên đoạn  1;2 lần lượt là: 
A. 0 và 1
2
 B. 0 và 3 C. 0 và 2 D. 0 và 1 
Câu 16: Chọn mệnh đề sai trong các mệnh đề sau: 
A. Nếu a là số thực không âm thì 3 4a a a 
B. Nếu n là số nguyên lẻ, 3n  và a, b là hai số thực bất kỳ thì 1. .n nn na a b a b  
C. Nếu n là số nguyên chẵn, 2n  và a, b là hai số thực dương bất kỳ thì 
2
2.
n n
nn
a a
ba b

 
D. Với mọi số thực a thì 4 4a a 
Câu 17: Tập xác định của hàm số 2log ( 1) log( 2)y x x    là: 
A.  2; B.  1; 2 C.    ; 1 2;    D.  
Câu 18: Tập xác định của hàm số  23log 4 3y x x   là: 
A.  ;1 B.  1;3 C.    ;1 3;   D.  3; 
Câu 19: Cho số thực a dương khác 1. Chọn khẳng định sai trong các khẳng định sau: 
A. loga a
  B. logaa    0  C. log 1 0a  D. 4log 4loga ab b 
Câu 20: Với 0, 1a a  , chọn mệnh đề sai trong các mệnh đề sau: 
A.  loga a  và logaa   , với mọi số thực 0  B.  log . log loga a ax y x y  , với mọi số thực ,x y 
C. log log loga a a
x x y
y
 
  
 
, với mọi số thực ,x y dương D. log 1 0a  
Câu 21: Với 0, 1a a  , chọn mệnh đề sai trong các mệnh đề sau: 
A.  
1log logaa b b 
 , với b là số thực dương và 0  
B. loglog
log
c
a
c
bb
a
 , với b là số thực dương và 0, 1c c  
C.  2log . 2.log loga a ax y x y  , với mọi số thực ,x y dương 
D. 1log
loga b
b
a
 , với mọi số thực b dương 
Câu 22: Chọn mệnh đề sai trong các mệnh đề sau: 
A.  log .loga bb a  với ,a b là các số thực dương khác 1 B. 9 3  
C.  
1log .logba b a 
 với ,a b là các số thực dương khác 1 và 0  D. Căn bậc hai của 9 bằng 3 hoặc 3 
Câu 23: Giá trị lớn nhất maxy của hàm số lny x trên nửa đoạn  0;1 : 
A. max 1y   B. max 10y  C. max 5y  D. max 0y  
Câu 24: Cho số thực a dương và khác 1. Tập giá trị của hàm số xy a trên tập xác định là: 
A.  B.  0;  C.  1; D.  1;  
Câu 25: Chọn mệnh đề sai trong các mệnh đề sau: 
A. Với mọi số thực 0a  và mọi số tự nhiên 1k  thì 2 0k a  
B. Mọi số thực dương đều có hai căn bậc chẵn và hai giá trị đó đối nhau 
C. Mọi số thực đều có duy nhất một căn bậc lẻ D. Với mọi số thực a và mọi số tự nhiên 1k  thì 2 1 0k a  
Câu 26: Tập xác định của hàm số 1
log 1
y
x


 là: 
A.  10; B.  10; C.  \ 10 D.  ;10 
Câu 27: Chọn khẳng định sai trong các khẳng định sau: 
A. 1 1 2
2 4
x
x     
 
 B. 1 1 0x xe
   C. 3 3x y x y   D. 1 0xe x   
Nguyễn Tích Đức - TCV Trang 3/9 - Mã đề thi 130 
Câu 28: Nghiệm của phương trình log 910 8 5x  là: 
A. 7
4
 B. 0 C. 1
2
 D. 5
8
Câu 29: Hàm số xy e x  đồng biến trên khoảng nào trong các khoảng sau: 
A.  0;  B.  ;  C.  ;0 D.  0;1 
Câu 30: Xét các hàm số    f x u x và    
1
2g x u x    có tập xác định lần lượt kí hiệu ,f gD D . Khẳng định đúng 
là: 
A. f gD D B. f gD D C.   0, ff x x D   D.   0, gg x D  
Câu 31: Chọn mệnh đề sai trong các mệnh đề sau: 
A. 
n
m nma a với mọi số thực 0a  và ,n m là hai số nguyên trong đó 2m  
B. a a
a

 

 với mọi số thực , ,a   và 0a  
C. 0 1a  với mọi số thực a D. 1 nn aa
 với mọi số thực 0a  
Câu 32: Chọn mệnh đề sai trong các mệnh đề sau: 
A. Hàm số logay x đồng biến trên  0; khi 1a  
B. Hàm số xy a đồng biến trên khoảng  0;  và nghịch biến trên khoảng  ;0 khi 0 1a  
C. Hàm số xy a nghịch biến trên tập số thực khi 0 1a  
D. Cả hai hàm số xy a và logay x đều đồng biến trên tập xác định nó khi 1a  
II. Thông hiểu 
Câu 33: Đạo hàm của hàm số 2 xy xe là: 
A. 2 xy xe  B.  2 1 xy x e   C.  2 1 xy x e   D.  1 xy x e   
Câu 34: Tập xác định của hàm số 2log
1
xy
x



 là: 
A.    ;1 2;   B.  1;2 C.  \ 1 D.  \ 1;2 
Câu 35: Với số thực 0a  , biểu thức 
  3 13 1
5 3 4 5.
a
a a


 
 được rút gọn thành: 
A. 1a B. a C. 2a D. 1 
Câu 36: Nghiệm của bất phương trình  21
2
log 5 7 0x x   là: 
A. 2 3x  B. 3x  C. 2x  D. 2x  hoặc 3x  
Câu 37: Tập xác định của hàm số 2log
1
xy
x



 là: 
A. 31;
2
 
 
 
 B.  1; C. 31;
2
 
  
 D.  \ 1 
Câu 38: Số nghiệm của phương trình 12 2 3x x  là: 
A. 0 B. 1 C. 2 D. 3 
Câu 39: Tập xác định của hàm số  ln 2 1xy   là: 
A.  0;  B. 1 ;
2
   
 C.  1; D.  ;0 
Câu 40: Theo thống kê dân số thế giới tính đến ngày 28/02/2016, dân số Việt Nam có 94 104 871 người và tỷ lệ tăng dân 
số là 1,07%. Hỏi đến ngày 28/02 của năm nào thì dân số Việt Nam vừa chớm vượt mốc 100 triệu người nếu tỷ lệ tăng dân 
số không đổi và không kể số người chết? 
A. năm 2021 B. năm 2023 C. năm 2022 D. năm 2024 
Câu 41: Tập xác định của hàm số  21
5
log 2y x x  là: 
A.  2;  B.    ;0 2;   C.  ;0 D.  0;2 
Nguyễn Tích Đức - TCV Trang 4/9 - Mã đề thi 130 
Câu 42: Gọi 1 2,x x là nghiệm của phương trình 9 3.3 2 0
x x   . Khi đó giá trị biểu thức  1 22 x x bằng: 
A. 2 B. 1 C. 6 D. 32log 2 
Câu 43: Hàm số xy e x  nghịch biến trên khoảng nào trong các khoảng sau: 
A.  0;  B.  ;  C.  ;0 D.  0;1 
Câu 44: Nếu log3 a thì log9000 được biểu thị theo a là: 
A. 2 3a  B. 2 3a  C. 23a D. 2a 
Câu 45: Số nghiệm của phương trình 12 2 3x x   là: 
A. 0 B. 1 C. 2 D. 3 
Câu 46: Tập xác định của hàm số  
1
2 32y x x  là: 
A.  ;1 B.  0; 2 C.  D.    ; 0 2;   
Câu 47: Số nghiệm của phương trình    23 3log 6 log 2 1x x    là: 
A. 0 B. 1 C. 2 D. 3 
Câu 48: Gọi 1 2,x x là nghiệm của phương trình 
2
2 2log 3log 2 0x x   . Khi đó giá trị biểu thức 3 1 3 2log logx x bằng: 
A. 32 3log 2 B. 2 C. 0 D. 33log 2 
Câu 49: Cho log 3a b  và log 2a c   . Giá trị của biểu thức  3 2 3loga a b c bằng: 
A. 9 B. 25
3
 C. 29
3
 D. 3 
Câu 50: Gọi 0x là nghiệm của phương trình    log 1 log 2 11 log 2x x    . Khi đó giá trị biểu thức log22 x bằng: 
A. 7 B. 2 C. 0 D. 1 
Câu 51: Cho hàm số 1ln
1
y
x


. Khi đó biểu thức . 1 yx y e   bằng: 
A. 2
1x 
 B. 1 C. 0 D. 2
1
x
x 
Câu 52: Cho log 3a b  và log 2a c   . Giá trị của biểu thức 
34 2
3
.loga
a b
c
 
 
 
 
 bằng: 
A. 12 B. 1
3
 C. 0 D. 5
3
Câu 53: Nếu log3 a thì biểu thức 
81
1
log 100
 biểu diễn theo a là: 
A. 4a B. 
8
a C. 2a D. 16a 
Câu 54: Cho 2log 2x  , giá trị của biểu thức 
2 3
2 1 4
2
log log logA x x x   bằng: 
A. 0 B. 2
2
 C. 1
2
 D. Một kết quả khác 
Câu 55: Gọi 0x là nghiệm của phương trình 
18 8 7 0x x    . Khi đó giá trị biểu thức 20170ln x bằng: 
A. 0 B. 2017 C. 2017e D. 1 
Câu 56: Hàm số lny x x  đồng biến trên khoảng nào trong các khoảng sau: 
A.  1; B.  0;1 C.  1;0 D.  ;  
Câu 57: Số nghiệm của phương trình 
22 7 52 1x x   là: 
A. 0 B. 1 C. 2 D. 3 
Câu 58: Với số thực 0a  , 1a  và x, y là hai số thực bất kì khác 0. Chọn khẳng định sai trong các khẳng định sau: 
A. log ( . ) log loga a ax y x y  B. 
2log ( ) 2loga ax x 
C. log ( ) log loga a axy x y  D. 
3log ( ) 3loga ax x 
Câu 59: Hàm số xy e x  đồng biến trên khoảng nào trong các khoảng sau: 
A.  ;  B.  0;1 C.  ;0 D.  0;  
Nguyễn Tích Đức - TCV Trang 5/9 - Mã đề thi 130 
Câu 60: Gọi 0x là nghiệm của phương trình 
2 1 23 3 108x x   . Khi đó giá trị biểu thức 32 0log x bằng: 
A. 1 B. 13 C. 3 D. 3 
Câu 61: Cho hàm số 
2xy e . Khi đó 2 .y x y  bằng: 
A. 
2
2 xe B. 
2
2 xxe C. 0 D. 
2
2 xe 
Câu 62: Hàm số lny x x  nghịch biến trên khoảng nào trong các khoảng sau: 
A.  1;0 B.  1; C.  0;1 D.  ;  
Câu 63: Giá trị nhỏ nhất miny và giá trị lớn nhất maxy của hàm số   2ln(1 )f x x  trên đoạn  0;1 lần lượt là: 
A. min 0y  và max ln 5y  B. min ln 2y  và max 0y  
C. min 0y  và ln 2 D. min ln 2y  và max ln 2y  
Câu 64: Giá trị nhỏ nhất miny và giá trị lớn nhất maxy của hàm số   2 lnf x x x trên đoạn  1; e lần lượt là: 
A. min 1y  và max 0y  B. min 0y  và max 1y  
C. min 0y  và max ln 2y  D. min 1y  và max ln 2y  
Câu 65: Giả thiết các hàm số   1ln
sin
f x
x
   
 
,   1 sinln
cos
xg x
x
   
 
,   1ln
cos
h x
x
   
 
 có đạo hàm trên miền K. Hàm 
số nào có đạo hàm bằng 1
cos x
? 
A.  h x B.  g x và  h x C.  f x D.  g x 
Câu 66: Tập xác định của hàm số   22 2x x  là: 
A.  1; 2 B.  C.  ;1 D.    ; 1 2;    
Câu 67: Theo thống kê dân số thế giới tính đến ngày 28/02/2016, dân số Việt Nam có 94 104 871 người và tỷ lệ tăng dân 
số là 1,07%. Hỏi đến thời điểm 28/02/2026, dân số Việt Nam có bao nhiêu người nếu tỷ lệ tăng dân số không đổi và 
không kể số người chết? 
A. 104 673 021,5 người B. 103 564 877 người C. 104 673 021 người D. 105 793 022 người 
Câu 68: Cho 2log 20  . Khi đó 20log 4 tính theo  là: 
A. 20
1log 4
2
 B. 20log 4 2

 C. 20log 4 2 D. 20
2log 4

 
Câu 69: Một người gửi số tiền 10 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không rút tiền ra khỏi 
ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Hỏi người đó được lĩnh bao nhiêu tiền (làm tròn 
đến hàng triệu) sau 14 năm nếu trong khoảng thời gian đó người này không rút tiền ra và lãi suất không đổi? 
A. 26 triệu B. 25 triệu C. 25,8 triệu D. 27 triệu 
Câu 70: Với ,x y là các số thực dương; thực hiện rút gọn các biểu thức 
5 5
4 4
4 4
x y xyP
x y



, 
2 2x y xyQ
x y



. Biểu thức nào 
có kết quả rút gọn là xy : 
A. không có B. chỉ mỗi P C. cả P và Q D. chỉ mỗi Q 
Câu 71: Sự tăng trưởng của một loại vi khuẩn tuân theo công thức . rtS A e , trong đó A là số lượng vi khuẩn ban đầu, r 
là tỉ lệ tăng trưởng ( 0)r  , t (giờ) là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 
con. Hỏi sau 10 giờ có bao nhiêu con vi khuẩn? 
A. 900 con B. 600 con C. 9000 con D. 500 con 
Câu 72: Trong các hàm số  
2
x xe ef x

 ,   2g x x x  ,   lnh x x x hàm số nào đạt cực tiểu tại điểm 0x  ? 
A.  g x B.  f x C.  h x D.  g x và  h x 
Câu 73: Cho số thực 0, 1a a  . Chọn khẳng định sai trong các khẳng định sau: 
A. 1 1ln
x x
   
 
 B.   .lnx xa a a  
C.    
 
log
.lna
u x
u x
u x a
    D.  sin sin .cos .lnx xa a x a  
III. Vận dụng 
Nguyễn Tích Đức - TCV Trang 6/9 - Mã đề thi 130 
Câu 74: Nếu  6 5 6 5x   thì x thỏa mãn: 
A. 1x  B. 1x   C. 1x   D. 1x  
Câu 75: Bất phương trình (0,5)log 0x m  nghiệm đúng với mọi x thuộc khoảng  2;  khi tham số m thỏa mãn: 
A. 1m   B. 1m   C. mọi m thuộc  D. 2m   
Câu 76: Biết 4 4 23x x  , giá trị của biểu thức 2 2x x bằng: 
A. 5 B. 5 hoặc 5 C. 5 D. 21 
Câu 77: Hệ số góc của tiếp tuyến với đồ thị hàm số 2xy  tại điểm  2log 3; 3M là: 
A. 3 B. 2.ln2 C. ln8 D. ln2 
Câu 78: Tập xác định của hàm số  2ln 4 3.2 4xy    là: 
A.  0;  B.  0;  C.  0;2 D.  
Câu 79: Với điều kiện 0a  , 1a  kết quả rút gọn của biểu thức 
 
 
4
3 32 43
1
a a a
A
a a a





 là: 
A. A a B. 
2
1
a aA
a



 C. A  1 D. A a  
Câu 80: Nếu 12log 6 a và 12log 7 b thì 2log 7 tính theo ,a b bằng: 
A. 
1
a
b
 B. 
1
a
b
 C. 
1
b
a
 D. 
1
a
a 
Câu 81: Cho hàm số 22 lny x x  . Xét các mệnh đề sau: 
(I): “Hàm số đồng biến trên khoảng 1 ;
2
   
 
” 
(II): “Hàm số nghịch biến trên khoảng 10;
2
 
 
 
” 
Chọn khẳng định đúng trong các khẳng định sau: 
A. (I) sai và (II) đúng B. (I) đúng và (II) sai C. (I) và (II) cùng sai D. (I) và (II) cùng đúng 
Câu 82: Nghiệm của bất phương trình    2 3 2 3log log 5x  là: 
A. 10
5
x  B. 1
5
x  C. 1
5
x  D. 0x  
Câu 83: Nghiệm của bất phương trình  2 1
2
log log 1 0x
 
  
  
 là: 
A. 2 B. 3
2
x  C. 32 3log 2 D. 
3
2
x  
Câu 84: Giả thiết tồn tại đạo hàm của hàm số   sin xf x x trên miền K. Kết quả tính đạo hàm  f x là: 
A.   sin sincos .lnx xf x x x x
x
    
 
 B.   sin 1.sinxf x x x  
C.   sin .ln .cosxf x x x x  D.  f x  0 
Câu 85: Nghiệm của bất phương trình    2 3 2 3log log 5x  là: 
A. 10
5
x  B. 1
5
x  C. 1
5
x  D. 0x  
Câu 86: Bất phương trình  21 2
2
log log 2 0x    có tập hợp nghiệm là: 
A.    1;1 2;   B.    1;0 0;1  C.  1;1 D. Một đáp án khác 
Câu 87: Cho 3log 15a  , 3log 10b  . Khi đó 3log 50 tính theo ,a b là: 
A.  2 1a b  B.  2 1a b  C.  2 1a b  D. 1 
Câu 88: Gọi 0x là nghiệm của phương trình      2 1 2 1log log 5 0x x    thì giá trị biểu thức 
04x bằng: 
Nguyễn Tích Đức - TCV Trang 7/9 - Mã đề thi 130 
A. 16 B. 32 C. 5 D. 2 
Câu 89: Cho hai số thực ,a b dương, 1a  . Tính giá trị biểu thức 
3
3
loga b
aP
b
 
   
 
 khi biết log 3a b  , kết quả là: 
A. 31 20 3
3
P  B. 31 20 3
3
P  
C. 23 16 3
3
P   D. không thuộc các kết quả trên 
Câu 90: Bất phương trình 0xe x m   nghiệm đúng với mọi x thuộc  khi tham số m thỏa mãn: 
A. 2m  B. mọi m thuộc  C. 1m  D. 1m  
Câu 91: Bất phương trình xe m nghiệm đúng với mọi x thuộc khoảng  0;  khi tham số m thỏa mãn: 
A. mọi m thuộc  B. 1m  C. 2m  D. 1m  
Câu 92: Phương trình .lnx x m có nghiệm thuộc đoạn  0;1 khi m thỏa mãn: 
A. 1 0m
e
   B. 10 m
e
  C. 1 0m
e
   D. 1 0m
e
   
Câu 93: Tập xác định của hàm số 25 5x xy   là: 
A.  0;  B.  0;  C.  1;  D.  1; 
Câu 94: Trong các biểu thức 
 33 2 1
2 1
a aP
a a


  , 
1 2
3 13 3Q a a a
 
  
 
 
; biểu thức nào có giá trị lớn hơn 1 với mọi số 
thực 0a  ? 
A. chỉ mỗi Q B. chỉ mỗi P C. không có D. cả P và Q 
Câu 95: Tập xác định của hàm số 2log 3log 2y x x   là: 
A.    ;10 100;   B.  ;10 C.  100; D.  10;100 
Câu 96: Cho các hàm số   1xf x e  ,   lng x x x  . Hàm số nào trong các hàm số đã cho đồng biến trên khoảng 
 0;1 : 
A.  f x B. không có C.  g x D. cả  f x ,  g x 
Câu 97: Xét hàm số 1ln
1
y
x


, khẳng định đúng là: 
A. 0yxy e   B. 1
2
yxy e   C. 1yxy e   D. 1yxy e    
Câu 98: Cho số thực 0a  , thực hiện rút gọn các biểu thức  
2 133
2 1
aP a
a


  , 
1 2
3 13 3Q a a a
 
  
 
 
. Biểu thức nào có 
kết quả rút gọn bằng 1a  ? 
A. chỉ mỗi Q B. cả P và Q C. chỉ mỗi P D. không có 
Câu 99: Cho 2log 3x  , giá trị của biểu thức 3823.log 9.logA x x  bằng: 
A. 5. 3 B. 6 3 C. 10 3 D. 2 3 
Câu 100: Với điều kiện ,x y là hai số thực dương, kết quả rút gọn của biểu thức 
5 5
4 4
4 2 24
x y xyA
x y



 là: 
A. 1 1
4 4
xyA
x y
 

 B. 1A  C. 1 1
4 4
xyA
x y


 D. 
1 1
4 4
1 1
2 2
xy x y
A
x y
 
 
 
 

Câu 101: Hệ số góc của tiếp tuyến với đồ thị hàm số lny x tại điểm M thuộc đồ thị và có tung độ bằng 1 là: 
A. 1e B. e C. 1 D. 0 
Nguyễn Tích Đức - TCV Trang 8/9 - Mã đề thi 130 
Câu 102: Cho hai số thực ,a b dương, thực hiện rút gọn các biểu thức 
3 .
.
a bP
a b
 , 
2 3. .a b a bQ
a b



. Biểu thức nào có 
kết quả rút gọn bằng .a b ? 
A. chỉ mỗi Q B. không có C. cả P và Q D. chỉ mỗi P 
Câu 103: Cho các hàm số   1lnf x
x
   
 
,   xg x e ,  h x x  . Hàm số nào trong các hàm số đã cho nghịch biến trên 
khoảng  0;  : 
A.  h x B.  f x C.  g x D. cả  f x ,  g x và  h x 
Câu 104: Số nghiệm thuộc khoảng  1;e của phương trình .ln 5xe x  là: 
A. 1 B. 2 C. 3 D. vô số 
Câu 105: Với điều kiện ,x y là hai số thực dương và x y , kết quả rút gọn của biểu thức 
5 5
4 4
4 2 24
x y xyA
x y



 là: 
A. 1A  B. 
1 1
4 4
1 1
2 2
xy x y
A
x y
 
 
 
 

 C. 1 1
4 4
xyA
x y


 D. 1 1
4 4
xyA
x y
 

Câu 106: Phương trình . xx e m  có nghiệm thuộc nửa khoảng  0;  khi m thỏa mãn: 
A. 0m  B. 0m  hoặc 1m
e
 C. 10 m
e
  D. 1m
e
 
Câu 107: Giả thiết tồn tại đạo hàm của hàm số   xf x x trên miền K. Kết quả tính đạo hàm  f x là: 
A.    1 lnxf x x x   B.    1 lnxf x x x   C.   .lnxf x x x  D.   1. xf x x x   
Câu 108: Với điều kiện 0a  , xét các biểu thức 
 
 
4
3 32 13
2
3 233
a a a
M
a a a





, 
 
4
3 32 13
2
33
2
.
a a a
N
a a

 , 
 
4
3 32 13
2
33 .
a a a
P
a a

 . 
Sắp các biểu thức theo giá trị tăng dần, kết quả là: 
A. N, M, P B. M, N, P C. M, P, N D. P, N, M 
Câu 109: Với hàm số  2ln 1y x  , xét các mệnh đề sau: 
(I): “Hàm số đồng biến trên khoảng  0;  ” 
(II): “Hàm số đạt cực tiểu tại điểm 0x  ” 
(III): “Hàm số đạt cực đại tại điểm 0x  ” 
Chọn khẳng định đúng trong các khẳng định sau: 
A. (I) và (II) cùng đúng, (III) sai B. (I) và (III) cùng đúng, (II) sai 
C. (II) và (III) cùng đúng, (I) sai D. (I), (II) và (III) cùng đúng 
Câu 110: Giải bất phương trình    2 1 2 12 3 2 3x x    . Tập nghiệm của bất phương trình này là: 
A. 1 ;
2
   
 
 B. 1 ;
2
   
 C. 1 ;3
2
 
  
 D. 1
2
 
 
 
Câu 111: Bất phương trình ln x x m  nghiệm đúng với mọi x thuộc đoạn  1;3 khi tham số m thỏa mãn: 
A. 1m  B. mọi m thuộc  C. 1m  D. 1m  
Câu 112: Nghiệm của bất phương trình 