Đề thi Toán giải tích 12 (chương 3)

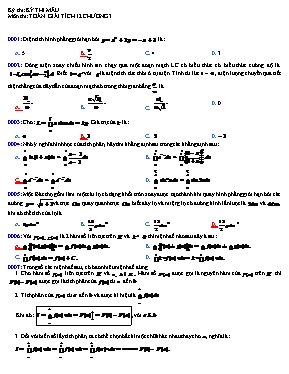
Kỳ thi: KỲ THI MẪU
Môn thi: TOÁN GIẢI TÍCH 12 CHƯƠNG 3
0001: Diện tích hình phẳng giới hạn bởi là:
A. 5	B. 	C. 4	D. 3
0002: Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức có biểu thức cường độ là. . Biết với là điện tích tức thời ở tụ điện. Tính từ lúc , điện lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian bằng là
A. 	B. 	C. 	D. 0
0003: Cho: . Giá trị của là:
A. 	B. 	C. 	D. 
0004: Nhờ ý nghĩa hình học của tích phân, hãy tìm khẳng định sai trong các khẳng định sau:
A. 	B. 
C. 	D. 
0005: Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường và trục quay quanh trục biết đáy lọ và miệng lọ có đường kính lần lượt là và , khi đó thể tích của lọ là
A. 	B. 	C. 	D. 
0006: Với là 2 hàm số liên tục trên và thì mệnh đề nào sau đây à sai:
A. 	B. 
C. 	D. 
0007: Trong số các mệnh đề sau, có bao nhiêu mệnh đề đúng
1. Cho hàm số liên tục trên và Hàm số được gọi là nguyên hàm của trên thì được gọi là tích phân của từ đến 
2. Tích phân của từ đến và được kí hiệu là .
 Khi đó: với 
3. Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ khác nhau thay cho , nghĩa là:
4. Nếu hàm số liên tục và không âm trên đoạn thì diện tích của hình thang cong giới hạn bởi đồ thị của trục và hai đường thẳng là: 
5. Nếu hàm số liên tục và không âm trên đoạn thì diện tích của hình thang cong giới hạn bởi đồ thị của trục và hai đường thẳng là: 
A. 2	B. 3	C. 1	D. 4
0008: Chọn phát biểu sai trong số các phát biểu sau
A. — Nếu là một nguyên hàm của trên thì họ nguyên hàm của hàm số trên là: 	B. — Nếu là một nguyên hàm của trên thì họ nguyên hàm của hàm số trên là: 
C. Cho hàm số xác định trên Hàm số được gọi là nguyên hàm của hàm số trên nếu: 	D. Cho hàm số xác định trên R Hàm số được gọi là nguyên hàm của hàm số trên nếu: 
0009: Diện tích hình phẳng tô đậm trong hình bên được tính theo công thức nào sau đây?
A. 	B. 
C. 	D. 
0010: Giá trị của 
A. 	B. 	C. 	D. 
0011: Kết quả của bằng:
A. 	B. 
C. 	D. 
0012: Tìm giá trị của tham số sao cho: và giới hạn bởi hai hình phẳng có cùng diện tích
A. 	B. 	C. 	D. 
0013: Tìm điều kiện của tham số để 
 là một nguyên hàm của hàm số 
A. 	B. 	C. 	D. 
0014: Diện tích hình phẳng giới hạn bởi trục tung và 2 đồ thị : là.
A. 	B. 	C. 	D. 
0015: Diện tích của hình phẳng giới hạn bởi: là:
A. 	B. 	C. 	D. 
0016: Cho và . Khi đó bằng
A. 	B. 	C. 	D. 
0017: Thể tích khối tròn xoay khi quay hình giới hạn bởi quay quanh trục là
A. 	B. 	C. 	D. 
0018: Cho nguyên hàm là.
A. 	B. 	C. 	D. 
0019: Hàm số có nguyên hàm là biểu thức nào sau đây,
 nếu biết đồ thị của hàm số đi qua điểm 
A. 	B. 	C. 	D. 
0020: Tính thể tích sinh ra khi quay quanh trục hình phẳng giới hạn bởi trục và Parabol 
A. 	B. 	C. 	D. 
0021: Tìm nguyên hàm sau 
A. 	B. 
C. 	D. 
0022: Diện tích hình phẳng giới hạn bởi đồ thị của: , trục và 2 đường thẳng là:
A. 	B. 	C. 	D. 
0023: Cho là một nguyên hàm của và đồ thị của qua thì bằng:
A. 	B. 	C. 	D. 
0024: Giá trị của là.
A. 	B. 	C. 	D. 
0025: Một vật chuyển động với vận tốc thì tăng tốc với gia tốc . Tính quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.
A. 	B. 	C. 	D.