Đề thi thử trung học phổ thông quốc gia môn: Toán - Đề 01

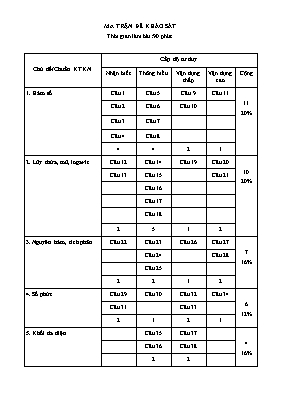
MA TRẬN ĐỀ KHẢO SÁT
Thời gian làm bài: 90 phút.	
Chủ đề/Chuẩn KTKN
Cấp độ tư duy
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Cộng
1. Hàm số
Câu 1
Câu 5
Câu 9
Câu 11
11
20%
Câu 2
Câu 6
Câu 10
Câu 3
Câu 7
Câu 4
Câu 8
4
4
2
1
2. Lũy thừa, mũ, logarit
Câu 12
Câu 14
Câu 19
Câu 20
10
20%
Câu 13
Câu 15
Câu 21
Câu 16
Câu 17
Câu 18
2
5
1
2
3. Nguyên hàm, tích phân
Câu 22
Câu 23
Câu 26
Câu 27
7
16%
Câu 24
Câu 28
Câu 25
2
2
1
2
4. Số phức
Câu 29
Câu 30
Câu 32
Câu 34
6
12%
Câu 31
Câu 33
2
1
2
1
5. Khối đa diện
Câu 35
Câu 37
4
16%
Câu 36
Câu 38
2
2
6.Mặt cầu, mặt nón, mặt trụ
Câu 39
Câu 41
Câu 42
4
Câu 40
2
1
1
7. Hình giải tích không gian
Câu 43
Câu 45
Câu 48
Câu 50
8
16%
Câu 44
Câu 46
Câu 49
Câu 47
2
3
2
1
Cộng
11
(22%)
20
(40%)
11
(22%)
8
(16%)
50
ĐỀ KHẢO SÁT
Cho hàm số có đồ thị (C). Khẳng định nào sau đây là khẳng định đúng?
	A. Đồ thị hàm số có tiệm cận đứng và tiệm cận ngang 
	B. Đồ thị hàm số có tiệm cận đứng và tiệm cận ngang 
	C. Đồ thị hàm số có tiệm cận đứng và tiệm cận ngang 
	D. Đồ thị hàm số có tiệm cận đứng và tiệm cận ngang 
Cho hàm số xác định, liên tục trên R và có bảng biến thiên :
-20
+ 0 - 0 +
0
Khẳng định nào sau đây sai ?
A. Hàm số đồng biến trên và . 
 B. Đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt
C. Hàm số đạt cực tiểu tại 
D. Hàm số nghịch biến trên 
 Hàm số cắt trục Ox tại mấy điểm
	A. 	B. 	C. 	D. 
Hàm số có 
	A. Điểm cực đại tại , điểm cực tiểu tại .
	B. Điểm cực tiểu tại , điểm cực đại tại .
	C. Điểm cực đại tại , điểm cực tiểu tại .
	D. Điểm cực đại tại , điểm cực tiểu tại .
Cho biết đồ thị sau là đồ thị của một trong bốn hàm số ở các phương án A, B, C, D. Đó là đồ thị của hàm số nào
A. 	B.
C.	D.
Đồ thị của hàm số có bao nhiêu đường tiệm cận.
	A. 1	B. 2	C. 3	D. 0
Tìm tập tất cả các giá trị của tham số để hàm số có đúng 1 cực trị.
A.	B. 	C. 	D. 
Tìm tất các giá trị của để hàm số đồng biến trên .
A. 	B. hoặc 
C. 	D. hoặc 
Gọi là tập giá trị của hàm số với . Khi đó bằng ?
A. .	B. .	C. .	D..
Đồ thị hàm số có hai điểm cực trị thì các hệ số có giá trị lần lượt là:
A. 	B.
C.	D.
Một công ty chuyên sản xuất container muốn thiết kế các thùng gỗ đựnng hàng bên trong dạng hình hộp chữ nhật không nắp, đáy là hình vuông, có thể tích là 62,. Hỏi các cạnh hình hộp và cạnh đáy là bao nhiêu để tổng diện tích xung quanh và diện tích mặt đáy là nhỏ nhất.
	A. Cạnh bên 2,5m. cạnh đáy 5m	B. Cạnh bên 4m. cạnh đáy m
	C. Cạnh bên 3m, cạnh đáy m	D. Cạnh bên 5m,cạnh đáy m
Cho là hai số thực dương khác và x và y là hai số thực dương. Tìm mệnh đề đúng trong các mệnh đề sau: 
	A.	B.
	C.	D. 
Tập nghiệm của phương trình: là.
	A. 	B.	C. 	D.
Cho , với . Mệnh đề nào dưới đây đúng ?
	A.	B.	C.	D.
Cho các số thực dương với . Khẳng định nào sau đây là khẳng định đúng?
A.	B.
C.	D. 
Tập nghiệm của bất phương trình là
A. 	B. 
C. 	D. 
Tính đạo hàm của hàm số .
A.	B. 
C.	D.
Tập xác định của hàm số là:
A.	B.
C.	D. 
Cường độ một trận động đất M(richer) được cho bởi công thức với A là biên độ rung chấn tối đa, và một biên độ chuẩn. Đầu thế kỉ 20, một trận động đất ở San Francisco có cường độ 8,3 độ Richer. Trong cùng năm đó, một trận động đất khác ở Nam Mỹ có biên độ mạnh gấp 4 lần. Cường độ của trận động đât ở Nam mỹ lấy gần đúng là.
A.	B. 	C.	D.
Tìm m để phương trình có đúng hai nghiệm .
A.	B.	C.	D. 
Cho các số thực thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức .
A.	B.	C. 	D.
Phát biểu nào sau đây là đúng?
	A. 	B. 
	C.	D.
Diện tích hình phẳng giới hạn bởi các đường và là:
A.	B.	C.	D.
Cho biết giá trị của là:
A.	B. 	C.	D.
Biết là một nguyên hàm của hàm số và . Tính .
A.	B. 	C.	D.
Tính với . Tính giá trị của .
A.	B.	C.	D.
Một vật đang chuyển động với vận tốc thì tăng tốc với gia tốc . Quãng đường vật đi được trong khoảng thời gian giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu?
A. 	B. 	C. 	D. 
Một gáo có hình nửa mặt cầu bán kính đựng nước có độ cao như hình vẽ. Tính thể tích nước trong gáo. 
A. (đvtt)	B.(đvtt)	C.(đvtt)	D.(đvtt)
x
yYyyx
Mx
4
OMx
2Mx
Điểm trong hình vẽ bên là điểm biểu diễn của số phức Tìm phần thực và phần ảo của số phức 
A. Phần thực là và phần ảo là.	
 B. Phần thực là 2 và phần ảo là 
C.Phần thực là 2và phần ảo là 	
 D. Phần thực là và phần ảo là 
Tìm số phức liên hợp của số phức . 
A. .	B. .	C. .	D. .
 Gọi và là hai nghiệm phức của phương trình . Tính giá trị của biểu thức 
A. .	B. .	C. .	D. .
Cho số phức thỏa mãn . Tính .
A.	B. 	C.	D.	
Trên mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện là đường có phương trình.
A. 	B.
C. 	D.
Cho số phức thỏa mãn Giá trị lớn nhất và giá trị nhỏ nhất của lần lượt là: 
	A. 10 và 4	B. 5 và 4	C. 4 và 3	D. 5 và 3
Tổng sổ đỉnh, số cạnh và số mặt của hình lập phương là:
	A. 8	B. 24	C. 16	D. 26 
Cho hình chóp có đáy là hình vuông cạnh và thể tích khối chóp bằng . Tính khoảng cách từ đến mặt phẳng .
A.	B.	C.	D.
Cho hình lăng trụ ABC.A’B’C’ có thể tích là. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó thể tích của khối chóp C’AMN là:
	A.	B.	C.	D.
Cho hình chóp S.ABCD đáy là hình vuông, Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Biết diện tích của tam giác SAB là. Thể tích khối chóp S.ABCD là:
	A.	B.	C.	D.
Cho hình nón,mặt phẳng qua trục và cắt hình nón tạo ra thiết diện là tam giác đều cạnh 2a. Tính thể tích của khối nón.
	A.	B.	C.	D.
Cho hình chữ nhật ABCD cạnh . Gọi M, N là trung điểm các cạnh AB và CD. Cho hình chữ nhật quay quanh MN, ta được hình trụ tròn xoay có thể tích bằng.
A.	B. 	C.	D.
Hình chóp S.ABC có đáy ABC là tam giác vuông tại A có và , , .Mặt cầu đi qua các đỉnh A,B,C,S có bán kính r bằng :
A.	 B.	C.	D.
30cm
35 cm
10 cm
Một cái mũ vải của nhà ảo thuật với các kích thước như hình vẽ sau. Hãy tính tổng diện tích vải cần có để làm nên cái mũ đó (không kể viền, mép, phần thừa).
A.	B. 
C.	D.
Cho bốn điểm . Xác định toạn độ trọng tâm của tứ diện .
A. 	B. 	C.	D. 
Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng 
	A.	B.	C.	D.
Cho hai điểm Phương trình của mặt cầu đường kính là:
	A.	B.
	C.	D. 
Phương trình tổng quát của qua A(2;-1;4), B(3;2;-1) và vuông góc với là:
	A.	B.
	C.	D. 
Trong không gian Oxyz, xác định các cặp giá trị (l, m) để các cặp mặt phẳng sau đây song song với nhau: ; .
	A.	B.	C.	D.
Cho điểm Viết phương trình mặt phẳng đi qua gốc tọa độ và cách một khoảng lớn nhất. 
	A.	B.
	C.	D.
Tìm điểm trên đường thẳng sao cho với 
	A. hoặc 
	B. hoặc 
	C. hoặc 
	D.Không có điểm nào thỏa mãn yêu cầu của bài toán
Trong không gian với hệ tọa độ xét các điểm với và Biết rằng khi m, n thay đổi, tồn tại một mặt cầu cố định tiếp xúc với mặt phẳng và đi qua . Tính bán kính R của mặt cầu đó?
A. 	B.	C.	D.