Đề thi thử THPT quốc gia Toán 2017 - Trường THPT Trần Quang Khải

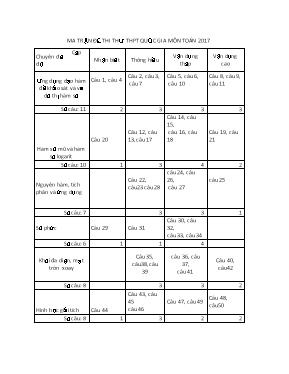
MA TRẬN ĐỀ THI THỬ THPT QUỐC GIA MÔN TOÁN 2017
Chuyên đề Cấp độ
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Câu 1, câu 4
Câu 2, câu 3,
 câu 7
Câu 5, câu 6,
 câu 10
Câu 8, câu 9,
câu 11
Số câu: 11 
2
3
3
3
Hàm số mũ và hàm số logarit
Câu 20
Câu 12, câu 13,câu 17
Câu 14, câu 15,
 câu 16, câu 18
Câu 19, câu 21
Số câu: 10
1
3
4
2
Nguyên hàm, tích phân và ứng dụng
Câu 22, câu23 câu 28
câu 24, câu 26,
 câu 27
câu 25
Số câu: 7
3
3
1
Số phức
Câu 29
Câu 31
Câu 30, câu 32,
câu 33, câu 34
Số câu: 6
1
1
4
Khối đa diện, mặt tròn xoay
Câu 35, câu38, câu 39
câu 36, câu 37,
câu 41
Câu 40, câu42
Số câu: 8
3
3
2
Hình học giải tích
Câu 44
Câu 43, câu 45
câu 46
Câu 47, câu 49
Câu 48, câu50
Số câu: 8
1
3
2
2
ĐỀ THI THỬ THPT QUỐC GIA MÔN TOÁN
Thờigianlàmbài: 90 phút.
Câu 1: Tiệmcậnngangcủađồthịhàmsố
A. y = 2 	B. y = - 2 	C. x = 3 	D. x = -2
Câu 2: Cho hàmsố: y = -x4 + 8x2 – 4. Chọnđápánđúng.
A. Hàmsốcócựcđạinhưngkhôngcócựctiểu
B. Đồthịhàmsốcắttrục Ox tại 2 điểmphânbiệt.
C. Hàmsốđạtcựctiểutại x = 0
D. Cả A và B đềuđúng
Câu 3: TọađộđỉnhcủaParabol: y = x2 – 4x + 1 là: 
A. (2; -3) 	B. (2;3) 	C. (-2;3) 	D. (0;2)
Câu 4: Cho hàmsố. Chọnphátbiểusai: 
A. Đồthịhàmsốcótiệmcậnđứng x = 1
B. Hàmsốkhôngcócựctrị
C. Hàmsốluônđồngbiến
D. Hàmsốkhôngcóđiểmuốn
Câu 5: Cho hàmsố y = x3 – 3x2 + mx + m – 2 
Tìm m đểhàmsốcócựcđạivàcựctiểu?
A. m > 3 	B. m ≤ 3 	C. m < 3 	D. m ≥ 3
Câu 6: Cho hàmsố y = x4 – 2x2 + 4 (C). Tìm m đểđồthịhàmsố (C) cắtđườngthẳng d: y = m tại 4 điểmphânbiệt?
A. 3 0
Câu 7: Cho hàmsố y = -x4 + 5x2 – 2 (C)
Hệsốgóccủatiếptuyếncủa (C) tạiđiểmcóhoànhđộ 1 là: 
A. 6 	B. 5 	C. 4 	D. 3
Câu 8: Vớigiátrịnàocủa m thìđồthịhàmsố:cắtđườngthẳng d: y = mx + 2m + 1 tại 2 điểmphânbiệtsaochochúngcáchđềutrục Ox.
A. m = -3 	B. m = 3 	D. m = 0
Câu 9: Vớigiátrịnàocủa m thìđồthịhàmsố y = x3 + 5x2 + mx + m – 5 có 2 điểmcựcđại, cựctiểunằmvề 2 phíatrụctung?
	A. m ≤ 0 	B. m ≥ 0 	C. m 0
Câu 10: Giátrịnhỏnhấtcủahàmsố y = x3 – 5x2 + 7x – 3 trên [0; 2] là: 
A. -3 	B. 0 	C. -1 	D. 3
Câu 11: Cho hàmsố: y = x3 – 2x2 + (1- m)x + m. Tìm m đểđồthịhàmsốcắttrụchoànhtại 3 điểmphânbiệt x1, x2, x3thỏamãnđiềukiện: 
	C. m ≤ 1 	
Câu 12: Vớia>0,a≠1, hãy chọnphátbiểusai:
A .Hàmsốy=logaxcótậpxácđịnhlà(0;+∞)
B .Hàmsốy=axnhậntrụchoànhlàmtiệmcậnngang.
C .Hàmsốy=axcótậpxácđịnhlà(0;+∞)
D .Hàmsốy=logaxvàhàmsốy=axđồngbiếnkhia>1.
Câu 13: Tậpxácđịnhcủahàmsốy=(2x-1)23là:
	A .[12;+∞)	B. R	C. (12;+∞)	D. R\[0;2]
Câu 14: Tậpnghiệmcủaphươngtrình5x-1+53-x=26 là:
	A . {3; 5}	B . {1; 3}	C . {2; 4}	D. ∅
Câu 15:Phươngtrìnhlog3(x2-x-5)=log3(2x+5)cótổngcácnghiệmlà:
	A . 3	B . 5	C . 2	D . -10
Câu 16: Tậpnghiệmcủabấtphươngtrìnhlog0,3(2x-5)≥0 là:
	A .[3;+∞)	B . (-∞;3]	C .(52;3]	D .[114;+∞)
Câu 17: Vớia>0,a≠1 chọnmệnhđềđúng:
	A .loga1=avàlogaa=0	B . logaxα=αlogaxvớix>0, α≠0
	C .logaxy= logax.logay	D. logaxcónghĩavớimọix.
Câu 18: Tậpnghiệmcủabấtphươngtrình :log22x-1-log12(x-2)≤1là:
	A .(2;+∞)	B . [52;2]	C .(2;52]	D. (2;3]
Câu 19: Cho log214=mhãy tính P=log4932theo m:
A .P=52m-2	B .P=3m+1	C .P=3m-2	D. P=1m-1	
Câu 20: Đạohàmcủahàmsốy=(x+1)e2x là?
	A .(2x+1)e2x	B. (2x+3)e2x	C .(x+2)e2x	D. e2x
Câu 21: Theo hìnhthứclãiképmộtngướigửi 100 triệuđồngvàongânhàngtheokỳhạnmộtnămvớilãisuất 1,75% ( giảsửlãisuấthàngnămkhôngthayđổi) thìsauhainămngườiđóthuvềđượctổngsốtiềnlà:
	A . 103,351 triệuđồng	B .103,530triệuđồng
	C .103,531triệuđồng	D .103,500 triệuđồng
Câu 22: Nguyênhàmcủahàmsốfx=sin3x.cosx là: (C là hằngsố)
	A .14sin4x+C	B .13cos3x+C	C .13sin3x+C	D .sin4x+C
Câu 23: Cho 01fxdx=m , hãytínhI=01f2xdxtheom:
	A . 2m	B .m2	C. 12 m	D. m
Câu 24: Diệntíchhìnhphẳnggiớihạnbởicácđườngy=x3-3x;y=x;x=2;x=-2 là?
	A . 4	B . 8	C. 2	D . 16
Câu 25: Nếuđặtu=1-x2thìtíchphân01x51-x2dx trở thành:
	A .01u1-u2du	B .10u1-u	C .01u2(1-u2)2du	D. 10u4-u2du
Câu 26: Thểtíchkhốitrònxoaysinhra do hìnhphẳnggiớihạnbởicácđườngy=sinx;y=0;x=0;x=π khi quay quanh trục ox là:
	A .π23	B .π22	C .π24	D .2π23
Câu 27: Biết F(x) lànguyênhàmcủahàmsốy=1x-1vàF(2)= 1. KhiđóF(3) bằngbaonhiêu?
	A . ln2+1	B 12	C .ln32	D. ln2
Câu 28: Giátrịtíchphân1exlnxdxbằng:
	A .e24	B. e24-1	C .e2+14	D. 12-e24
Câu 29:Cho z1=2+5i; z2=1-i. Phầnthựccủaz1.z2là:
	A . 7	B . -3	C . 3	D . 2
Câu 30: Tìmmôđuncủaz=-8-3i1-i
	A .1462	B .1462	C .732	D .1464
Câu 31: Cho z1=1+2i; z2=2-3i. Tìmphầnảocủaz1-2z2
	A . 8i	B .8 	C . 3i	D . 3
Câu 32: Phươngtrình4z+1=1-i có nghiệmlà:
	A .z=2-i	`B .z=3+2i	C .z=5-3i	D .z=1+2i
Câu 33: Cho sốphức z thoảmãn2-iz=3-4i . Tìmmôđuncủaw=2i-3z
	A . 37	B .35	C. 13	D . 5
Câu 34: Gọiz1,z2làhainghiệmcủaphươngtrìnhz2+2z+26=0 . TìmA=z12+z22-z1.z2
	A . 54	B . -56 	C. 52	D . 26
Câu 35: Cho hìnhchóp S.ABC đáylàDABC vuôngcântại A với AB = a, SA vuônggócvớimặtđáy. SA = 3a. Thểtíchkhốichóp SABC là: 
A. 	B. a3	C. 	D. 
Câu 36: Cho hìnhchóp S.ABCD, đáy ABCD làhìnhvuôngcạnh 3a, mặtbên SAB là tam giácđềunằmtrongmặtphẳngvuônggócvớiđáy. Thểtíchkhốichóp S.ABCD là: 
Câu 37: Cho hìnhchóp S.ABCD đáylàhìnhchữnhậtcó AB = 2a, BC = a. Hìnhchiếuvuônggóccủa S lênđáylàđiểm A. Gócgiữa SB vàđáylà 450. Tínhthểtíchkhốichóp S.ABCD.
A. a3	B. 	C. 4	D. a3
Câu 38: Cho tứdiện ABCD có AB, AD, AC, đôimộtvuônggócvớinhauvàcóđộdàilầnlượtlàa,b,c thìcóthểtíchlà:
	A .abc3	B .abc6	C .abc	D .abc2
Câu 39: Quay hìnhvuôngcócạnha xung quanh mộtcạnh. Thểtíchkhốitrụđượctạothànhlà:
	A .13πa3	B .2πa3	C .πa3	D. 3πa3
Câu 40: Mặtcầungoạitiếphìnhchóptứgiácđềucótấtcảcáccạnhđềubằnga thìcóbánkínhlà:
	A .a22	B .a2	C. a2	D. a32
Câu 41: Diệntíchxungquanhcủahìnhnóncóthiếtdiện qua trụclà tam giácđềucạnha là: 
	A .πa2	B .πa24	C .πa22	D. 2πa2
Câu 42: Thểtíchkhốinóncóthiếtdiện qua trụclà tam giácvuôngcócạnhgócvuônglà2a là:
	A .2πa32	B. 8πa323	C .2πa323	D .2πa33
Câu 43: TìmbánkínhcủamặtcầucótâmI( 1; 2; 4) biếtmặtcầutiếpxúcvớimp: 2x – y + 2z – 5 = 0:
	A . 3	B . 1	C . 1/3 	D . 2/3 
Câu 44: Mặtcầu (S) cóphươngtrình : x2 + y2 + z2 - 2x +4y – 6z – 2 = 0 cótâm I vàbánkính R làbaonhiêu?
	A .I(1;-2;3), R= 14	B . I(-1;2;-3), R= 14
	C .I(1;-2;3), R= 4 	D . I(-1;2;-3), R= 4
Câu 45: Cho mặtphẳng( P) : 2x – y + z – m = 0 vàđiểm A(1; 1; 3) . Tìm m đểkhoảngcáchtừđiểmAđếnmặtphẳng (P) là6
	A .m=-2m=4	B. m=3m=9	C .m=-2m=10	D .m=-3m=12
Câu 46: Mặtphẳng (P) qua cácđiểmA(-2; 0; 0), B(0; 3; 0), C(0; 0; 4) cóphươngtrìnhlà:
	A .x2+y3+z4=1	B .x2-y3-z4=1
	C .x-2+y3+z4=0	D .x-2+y3+z4=1
Câu 47: Toạđộgiaođiểmcủamặtphẳng (P) : x – 3y + z = 0 vàđườngthẳng d x=1+2ty=2-tz=-1+tlà:
	A . (1; 2; -1)	B . (0; -1; -3)	C . (-1; 3; -2)	D .( 3; 1; 0)
Câu 48: Trongkhônggianchođườngthẳng d: x1=y-12=z+1-1vàA(1; 1; -2), B(-1; 0; 2). Viếtphươngtrìnhđườngthẳng∆ qua A, vuônggócvới d saochokhoảngcáchtừ B đếnđườngthẳng∆ lànhỏnhất?
	A .x-1-2=y-15=z+28	B .x+1-2=y+15=z-28
	C .x-12=y-15=z+28	D .x+21=y-51=z-8-2
Câu 49.Tìmtoạđộtiếpđiểmcủamặtcầu (S): x2 + y2 + z2 – 2x + 4y – 2z – 8 = 0 vàmặtphẳng (P): 2x + 3y + z – 11 = 0?
	A . (-3; 1; 2)	B. (3; 1; 2)	C.(0; 0; 11)	D.(-1; 2; 15)
Câu 50: Cho đườngthẳng d cóphươngtrình: x= ty=-1+2tz=1vàđiểmA(-1; 2; 3)
Viếtphươngtrìnhmặtphẳng (P) chứađườngthẳng d saochokhoảngcáchtừ A đếnmặtphẳng (P) bằng 3?
	A . 2x + y +2z = 0	B .2x - y –2z + 1 = 0 	
	C . 2x – y – 2z + 2 = 0	D . 2x +y +2z – 5 = 0
 _hết_
Đápán
1B
6A
11A
16C
21C
26B
31B
36A
41C
46D
2C
7A
12C
17B
22A
27A
32D
37C
42C
47D
3A
8A
13C
18C
23C
28C
33A
38B
43B
48A
4C
9C
14B
19A
24B
29A
34D
39C
44C
4B
5C
10A
15A
20B
25C
30B
35A
40A
45C
50B