Đề thi thử THPT quốc gia môn Toán - Trường THPT Nguyễn Thái Học

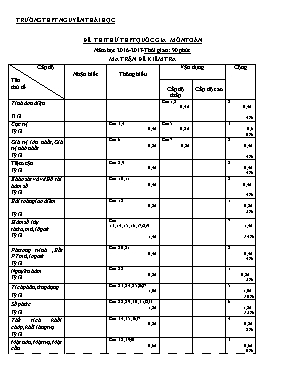
TRƯỜNG THPT NGUYỄN THÁI HỌC
ĐỀ THI THỬ THPT QUỐC GIA MÔN TOÁN 
Năm học 2016-2017-Thời gian : 90 phút
MA TRẬN ĐỀ KIỂM TRA
 Cấp độ
Tên 
chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Tính đơn điệu
Tỉ lệ 
Câu 1,2
0,4 đ
2 
 0,4đ
4%
Cực trị
Tỷ lệ
Câu 3,4
0,4đ
Câu 5
0,2 đ
3
0,6
6%
Giá trị lớn nhất,Giá trị nhỏ nhất
Tỷ lệ 
Câu 6
0,2đ
Câu 7
0,2đ
2
0,4đ
4%
Tiệm cận 
Tỷ lệ
Câu 8,9
0,4đ
2
0,4đ
4%
Khảo sát và vẽ Đồ thi hàm số
Tỷ lệ
Câu 10,11
0,4đ
2 
 0,4đ
4%
Bài toán giao điểm
Tỷ lệ
Câu 12
0,2đ
1
0,2đ
2%
Hàm số lũy thừa,mũ,lôgarit
Tỷ lệ
Câu 13,14,15,16,17,18,19
1,4đ
7
1,4đ
14%
Phương trình ,Bất PT mũ,logarit
Tỷ lệ
Câu 20,21
0,4đ
2
0,4đ
4%
Nguyên hàm 
Tỷ lệ
Câu 22
0,2đ
1 
 0,2đ
2%
Tích phân,ứng dụng
Tỷ lệ
Câu 23,24,25,26,27
1,0đ
5
 1,0đ
10%
Số phức
Tỷ lệ
Câu 28,29,30,31,32,33
1,2đ
6
 1,2đ
12%
Thể tích khối chóp,khối lăng trụ 
Tỷ lệ
Câu 34,35,36,37
0,8đ
4
0,8đ
8%
Mặt nón,Mặt trụ,Mặt cầu
Tỷ lệ
Câu 38,39,40
0,6đ
3
0,6đ
6%
Hệ tọa độ
Tỷ lệ
Câu 41,42
0,4đ
2
0,4đ
4%
Phương trình mặt phẳng
Tỷ lệ
Câu 43,44,45,46
0,8đ
4
0,8đ
8%
Phương trình mặt cầu
Tỷ lệ
Câu 47,48
0,4đ
2
0,4đ
4%
Phương trinh đường thẳng
Tỷ lệ
Câu 49,50
0,4đ
2
0,4đ
4%
Tổng số câu 
Tổng số điểm
Tỉ lệ 
46
9,2đ
92%
4
0,8đ
8%
50
10đ
100%
ĐỀ ÔN TẬP THI THPT QUỐC GIA
Câu 1 Tìm m để hàm số đồng biến trên 
Câu 2: Giá trị của m để hàm số nghịch biến trên là:
	a. 	b. 	c. 	d. 
Câu 3 Hàm số nào sau đây không có cực đại và cực tiểu: 
A.y = – 2x3 – x	B. y = –2x3 + x	C. y = 2x3 – x	D. y = 2x3 – 2x
Câu 4 Hàm số đạt cực đại tại:
A. x =1	B. x = –1	C. 	D. 
Câu 5. Cho hàm số 
Tìm m để hàm số có hai điểm cực trị tại x1 và x2 sao cho 
A. 	B. 	C. 	D. 
Câu 6: Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên 
	A. 8	B. 20	C. 	D. 33
Câu 7: Để thiết kế một chiếc bể cá hình hộp chữ nhật có chiều cao là 60cm, thể tích . Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70000 VNĐ/m2 và loại kính để làm mặt đáy có giá thành 100000 VNĐ/m2. Tính chi phí thấp nhất để hoàn thành bể cá.
	A. 320000 VNĐ.	B. 32000 VNĐ.	C. 832000 VNĐ.	D. 83200 VNĐ.	
Câu 8: Đồ thị hàm số có tâm đối xứng là điểm có tọa độ
	a. 	b. 	c. 	d. 
Câu 9: Số đường tiệm cận của đồ thị hàm số : là : 
A. 3 B. 2 C. 1 D. 4 
Câu 10: Đồ thị hàm số nào sau đây có đồ thị như hình vẽ bên?
A. 	B. 	C. 	D. 
Câu 11
 Đâu là hình dạng của đồ thị 
A. 	B
C. 	D 
Câu 12: Cho hàm số và đường thẳng . Đường thẳng cắt (C) tại hai điểm phân biệt A, B sao cho độ dài AB ngắn nhất thì giá trị của m là:
	A. 	B. 	C. 	D. Không tồn tại m
Câu 13: Tìm tất cả các giá trị thực của m để hàm số xác định trên R.
	A. 	B. 	C. 	D. 
Câu 14: Cho a, b là các số thực dương thỏa . Tính 
	A. 	B. 	C. 	D. 
Câu 15: Cho . Hãy biểu diễn theo a.
	A. 	B. 	C. 	D. 
Câu 16 :Đạo hàm của hàm số là:
A.	B. 	C. 	D. 
Câu 17 : Đạo hàm hàm số là
A. 	B. 	C. 	D. 
C©u18: NÕu (a > 0, a ¹ 1) th× x b»ng:
	A. 	B. 	C. 	D. 3
C©u19: Gi¶ sö ta cã hÖ thøc a2 + b2 = 7ab (a, b > 0). HÖ thøc nµo sau ®©y lµ ®óng?
	A. 	B. 
	C. 	D. 4
Câu 20: Giải bất phương trình 
	A. 	B. 	C. 	D. 
C©u 21: Giải ph­¬ng tr×nh: :
	A.x=-3	B. x=2	C. x=3	D. x=-2
Câu 22: Tìm nguyên hàm của hàm số 
	A. 	B. 
	C. 	D. 
Câu 23: Tính tích phân .
	A. 	B. 	C. 	D. 
Câu 24: Tính diện tích hình phẳng giới hạn bởi đường thẳng và đồ thị hàm số .
	A. 	B. 4	C. 	D. 3
Câu 25: Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi , quanh trục hoành là:
	A. (đvtt)	B. (đvtt)	C. (đvtt)	D. (đvtt)
Câu 26: Nguyên hàm của hàm số thỏa mãn là:
B. 
C. 
D. 
Câu 27: Tính tích phân 
A. 
B. 
C. 
D. 
Câu 28: Tính mô-đun của số phức z thỏa .
	A. 	B. 	C. 	D. 
Câu 29: Có bao nhiêu số phức z thỏa điều kiện 
	A. 1	B. 2	C. 3	D. 4
Câu 30: Cho số phức biết . Khẳng định nào sau đây là khẳng định đúng ?
	A. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường tròn
	B. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường elip.
	C. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là 2 điểm.
	D. Tập hợp điểm biểu diễn số phức w trên mặt phẳng phức là một đường thẳng.
Câu31: Cho số phức z = x + yi ¹ 1. (x, y Î R). Phần ảo của số là: 
	A. 	B. 	C. 	D. 
Câu32: Cho số phức z = a + a2i với a Î R. Khi đó điểm biểu diễn của số phức z nằm trên:
	A. Đường thẳng y = 2x	B. Đường thẳng y = -x + 1
	C. Parabol y = x2	D. Parabol y = -x2
Câu33: Trong C, Cho phương trình 7z2 + 3z +2 = 0 có 2 nghiệm z và z’. Khi đó tổng các nghiệm của phương trình là
 A. 3/7 B. -3/2 C.-3/7 D. -3/4
Câu 34: Cho khối chóp S.ABCD, có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy. Tính thể tích V khối chóp biết 
	A. 	B. 	C. 	D. 
Câu 35: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với mp đáy. Thể tích khối chóp S.ABCD là:
	A. 	B. 	C. 	D. 
Câu 36: Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên A’B tạo với đáy một góc 450. Thể tích khối lăng trụ ABC.A’B’C’ là:
	A. 	B. 	C. 	D. 
Câu 37: Cho lăng trụ đứng ABC.A’B’C’, có đáy ABC là tam giác vuông tại B. Tính diện tích toàn phần S của hình trụ tròn ngoại tiếp lăng trụ đứng ABC.A’B’C’ (như hình vẽ bên), biết rằng .
	A. 	B. 
	C. 	D. 
Câu 38: Cho hình chóp S.ABC có , đường cao . 
Tính bán kính r của mặt cầu ngoại tiếp hình chóp S.ABC.
	A. 	B. 	C. 	
 D. 
Câu 39: Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB = a, BC = a , SA vuông góc với đáy và cạnh bên SC hợp với đáy một góc 450 . Khoảng cách từ điểm A đến mặt phẳng (SBD) tính theo a bằng: 
A B C D 	
Câu 40. Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Diện tích xung quanh của hình nón đó là :
A. 	 B. C. D. 
Câu 41: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với . Chu vi của tam giác ABC bằng:
	A. 	B. 	C. 	D. 
Câu 42: Trong không gian Oxyz, cho bốn điểm . Hỏi khẳng định nào sau đây là khẳng định đúng ?
	A. Bốn điểm A, B, C, D là bốn điểm của một hình vuông.
	B. Bốn điểm A, B, C, D là bốn điểm của một hình chữ nhật.
	C. Bốn điểm A, B, C, D là bốn điểm của một hình thoi.
	D. Bốn điểm A, B, C, D là bốn điểm của một tứ diện.
Câu 43: Mặt phẳng (P) đi qua điểm và vuông góc với đường thẳng có phương trình là:
	A. 	B. 
	C. 	D. 
Câu 44: Trong không gian với hệ tọa độ Oxyz, cho điểm và hai mặt phẳng , . Viết phương trình mặt phẳng (R) đi qua A và vuông góc với hai mặt phẳng .
	A. 	B. 
	C. 	D. 
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho 2 mặt phẳng và . Tìm giá trị thực của m để mặt phẳng (P) vuông góc với mặt phẳng (Q).
	A. 	B. 	C. 	D. 
Câu 46: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng . Trong các đường thẳng sau đường thẳng nào song song với mặt phẳng (P).
	A. 	B. 
	C. 	D. 
Câu 47: Mặt cầu tâm I(a;b;c) bán kính R có tâm thuộc mặt phẳng x + y + z 2 = 0 và đi qua 3 điểm A(2; 0; 1), B(1; 0; 0), C(1; 1; 1).Tìm (a + 2b + 3c).R 
A. 12	B. 8	C. 6	D. 4
Câu 48: 
Cho hai đường thẳng và 
Trong các mệnh đề sau, mệnh đề nào đúng?
d1 cắt d2 B. d1 và d2 chéo nhau C. d1 trùng d2 D. d1 // d2
C©u 49 : 
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và mặt phẳng (P): 
2x – y + 2z + 1 = 0. Phương trình mặt cầu tâm A tiếp xúc với mặt phẳng (P) là:
A.
: (x – 2)2 + (y –1)2 + (z – 1)2 = 4
B.
 (x –+2)2 + (y – 1)2 + (z – 1)2 = 9
C.
: (x – 2)2 + (y –1)2 + (z – 1)2 = 3
D.
: (x – 2)2 + (y – 1)2 + (z – 1)2 = 5
C©u 50 : 
Trong không gian với hệ tọa độ vuông góc Oxyz, cho mặt phẳng
(P) : x + 2y + z – 4 = 0 và đường thẳng Phương trình đường thẳng ∆ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d là: 
A.
B.
C.
D.
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
A
B
A
A
A
A
D
B
A
A
11
12
13
14
15
16
17
18
19
20
A
C
B
B
A
D
C
C
B
A
21
22
23
24
25
26
27
28
29
30
C
D
B
A
D
D
A
A
B
D
31
32
33
34
35
36
37
38
39
40
B
C
C
A
D
D
A
C
D
A
41
42
43
44
45
46
47
48
49
50
A
D
B
B
B
A
D
A
D
A