Đề thi thử THPT quốc gia môn Toán học khối 12

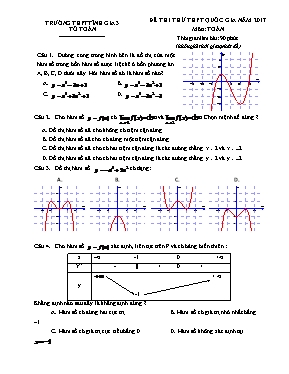
TRƯỜNG THPT TĨNH GIA 3
TỔ TOÁN
------------------------
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2017
Môn: TOÁN
Thời gian làm bài: 90 phút 
(không kể thời gian phát đề)
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
 A. B. 
 C. D. 
Cho hàm số có và . Chọn mệnh đề đúng ?
 A. Đồ thị hàm số đã cho không có tiệm cận đứng.
 B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
 C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 2 và x = -2.
 D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y = 2 và y = -2.
Đồ thị hàm số có dạng:
A.
B.
C.
D.
Cho hàm số xác định, liên tục trên R và có bảng biến thiên :
x
-∞ -1 0 +∞
Y’
 - || + 0 +
y
 + ∞ 
 -1
Khẳng định nào sau đây là khẳng định đúng ?
 	A. Hàm số có đúng hai cực trị.	B. Hàm số có giá trị nhỏ nhất bằng -1.
C. Hàm số có giá trị cực tiểu bằng 0.	D. Hàm số không xác định tại .
Hàm số có giá trị cực đại là ?
 A. . 	B. .	C. .	D. .
Khoảng đồng biến của hàm số là: 
 A. 	B. 	C. 	D. 
Cho và . Tìm mệnh đề đúng trong các mệnh đề sau: 
 A. có nghĩa với . 	B. và 
 C. .	D. ()
Giá trị lớn nhất của hàm số trên đoạn là:
 A. 	B. -2	C. 3	D. 	
Đặt . Hãy biểu diễn theo và 
 A. 	 	B. 	C. 	D. 
Khối bát diện đều có các mặt là :
 A. Hình vuông 	B. Tam giác đều 
 C. Hình chữ nhật 	D. Tam giác vuông
Đặt . Hãy biểu diễn theo .
 A. 	B. 	C. 	D. 
Cho (H) là khối lập phương có độ dài cạnh bằng 3cm. Thể tích của (H) bằng:
 A. 27cm3 	B. 27cm2 	C. 9cm3 	D. 3cm3 
Cho Giá trị của biểu thức bằng ?:
 A. 	B. 	C. 	D. 3
Cho (H) là khối lăng trụ có chiều cao bằng 3a, đáy là hình vuông cạnh a . Thể tích của (H) bằng:
 A. a3 	B. 2a3 	C. 3a3 	D. 4a3 
Cho . Giá trị của biểu thức bằng ?
 A. 	B. 5	C. 7	D. 
Biểu thức viết dưới dạng lũy thừa với số mũ hữu tỉ là: 
 A. 	B. 	C. 	D. 
 Tìm tất cả các giá trị thực của để biểu thức có nghĩa.
 A. 	B. 	C. 	D. 
Cho ABC.A’B’C’ là khối lăng trụ đứng có A’B=a, AB=a, đáy ABC có diện tích bằng 3a2. Thể tích của khối lăng trụ ABC.A’B’C’ bằng:
 A. a3 	B. 2a3 	C. 4a3 	D. 6a3 
Nếu độ dài các cạnh của khối hộp chữ nhật tăng lên 3 lần thì thể tích của khối hộp chữ nhật sẽ tăng lên:
 A. 3 lần 	B. 9 lần 	C. 27 lần 	D. 81 lần 
Cho (H) là khối hộp chữ nhật có độ dài cạnh bằng a, 2a, 3a. Thể tích của (H) bằng:
 A. a3 	B. 2a3 	C. 4a3 	D. 6a3 
Đường thẳng cắt đồ thị hàm số tại điểm có tọa độ thì: 
 A. .	 	B. .	 	C. .	D. .
Cho khối chóp (H) có thể tích là 2a3,đáy là hình vuông cạnh a. Độ dài chiều cao khối chóp (H) bằng:
 A. 4a 	B. 3a 	C. 2a 	D. a
Cho khối lăng trụ (H) có thể tích là 4a3, đáy là tam giác vuông cân có độ dài cạnh huyền bằng a. Độ dài chiều cao khối lăng trụ (H) bằng:
 A. 2a 	B. 4a 	C. 6a 	D. 8a
Giá trị lớn nhất của hàm số trên đoạn bằng. 
 A. 	B. 4 	C. 	D. 
Nếu độ dài chiều cao của khối chóp tăng lên 5 lần ,diện tích đáy không đổi thì thể tích của khối chóp sẽ tăng lên :
 A. 5 lần 	B. 10 lần 	C. 15 lần 	D. 20 lần 
Cho hàm số có đồ thị (C). Tiếp tuyến với đồ thị (C) tại điểm có hệ số góc lớn nhất, có phương trình là: 
 A. . 	B. . 	C. . 	D. .
Hàm số có đúng một cực trị khi và chỉ khi:
 A. 	B. 	C. 	D. 
Tìm tất cả các giá trị thực của tham số m để của hàm số có ba điểm cực trị là ba đỉnh của một tam giác vuông.	
 A. . 	 	B. . 	 	C. . 	D. .
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số có đúng một đường tiệm cận ngang.
 A. Không có giá trị nào của m thỏa mãn.	B. .	
 C. . 	D. .
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên 
 A. . 	B. . 	C. . 	D. .
Cho một tấm nhôm hình chữ nhật có chiều dài bằng 12 cm và chiều rộng bằng 10 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
 A. . 	B. . 	
 C. . 	D. .
Cho hai số thực a và b, với . Khẳng định nào dưới đây là đúng ?
 A. 	B. 	
 C. 	D. 
Hàm số không có cực trị khi và chỉ khi:
 A. 	B. 	C. 	D. 
Gọi I là giao điểm hai đường tiệm cận của hypebol (H): . Tiếp tuyến với đồ thị (H) tại điểm M(0; -1) cắt hai đường tiệm cận của (H) tại hai điểm A và B. Khi đó diện tích tam giác ABI bằng: 
 A. 8 đvdt. 	B. 6 đvdt. 	C. 4 đvdt. 	D. 2 đvdt.
Tìm các giá trị nguyên của tham số m để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng
 A. 	B. 	C. 	D. 
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm sốcó các cực trị đều nằm trên các trục tọa độ.
 A. 	B. 	C. D. 
Cho thỏa mãn . Chọn mệnh đề đúng.trong các mệnh đề:
 A. 	B. 	
 C. 	D. 
Cho khối lăng trụ ABC.A’B’C’ , M thuộc cạnh AA’ sao cho MA=3MA’. Tỉ số thể tích của khối lăng trụ ABC.A’B’C’ và thể tích khối chóp M.A’B’C’ bằng:
 A. 4 	B. 8 	C. 12 	D. 18
Một người gửi tiết kiệm ngân hàng, mỗi tháng gửi 1 triệu đồng, với lãi suất kép 1%/tháng. Gửi được hai năm 6 tháng người đó có công việc nên đã rút toàn bộ gốc và lãi về. Số tiền người đó rút được là:
 A. (triệu đồng).	B. (triệu đồng).
 C. (triệu đồng).	D. (triệu đồng).
Cho khối chóp S.ABC có SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với (ABC), AB=2a và tam giác ABC có diện tích bằng 3a2. Thể tích khối chóp S.ABC bằng:
 A. a3 	B. 3a3 	C. 6a3 	D. 2a3 
Cho khối chóp S.ABC , M là trung điểm của cạnh SA. Tỉ số thể tích của khối chóp S.MBC và thể tích khối chóp S.ABC bằng:
 A. 	B. 	C. 	D. 1
Cho khối chóp S.ABC ; M và N lần lượt là trung điểm của cạnh SA, SB; thể tích khối chóp S.MNC bằng a3. Thể tích của khối chóp S.ABC bằng:
 A. a3 	B. 4a3 	C. 8a3 	D. 12a3	
Cho hình lăng trụ đứng ABC.A’B’C’ có góc giữa A’B và (ABC) bằng 450; đáy ABC là tam giác vuông cân tại A và BC=2a. Thể tích khối lăng trụ ABC.A’B’C’ bằng : 
 A. a3 	B. 2a3 	C. 3a3 	D. 4 a3
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S trên (ABC) là điểm H thuộc cạnh AB sao cho HA=2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 600. Thể tích khối chóp S.ABC bằng: 
 A. a3 	B. a3 	C. a3 	D. a3 
Cho khối chóp S.ABCD có SA(ABCD), SB=a và ABCD là hình vuông cạnh a. Thể tích khối chóp S.ABCD bằng:
 A. a3 	B. a3 	C. a3 	D. 2a3
Cho khối chóp S.ABC , M là trung điểm của cạnh BC. Thể tích của khối chóp S.MAB là 2a3 . Thể tích khối chóp S.ABC bằng:
 A. 4a3 	B. 2a3 	C. a3 	D. a3
Cho hình chóp S.ABCD có SA (ABCD), SB=a ; ABCD là hình thoi cạnh a và góc = 300. Thể tích khối chóp S.ABCD bằng: 
 A. a3 	B. a3 	C. a3 	D. a3 
Cho hình chóp S.ABC có SA (ABC), góc giữa SB và (ABC) bằng 600 ; tam giác ABC đều cạnh a. Thể tích khối chóp S.ABC bằng: 
 A. a3 	B. a3 	C. a3 	D. a3
Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên tập xác định của nó.
 A. 	B. 	C. 	D. 
Cho hình chóp có đáy là hình vuông cạnh .Gọi lần lượt là trung điểm của . Gọilà trung điểm của . Tam giác là tam giác đều và vuông góc với mp() .Khoảng cách của hai đường thẳng chéo nhau và theo .
 A. 	B. 	C. 	D. 	
--------- Hết --------
Thí sinh không sử dụng tài liệu.
Họ và tên: ................................................................ SBD: .......................... Lớp: ..................