Đề thi thử THPT chuyên Lê Thánh Tông - Quảng Nam môn Toán học

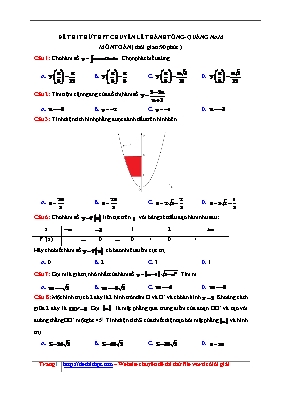
ĐỀ THI THỬ THPT CHUYÊN LÊ THÁNH TÔNG- QUẢNG NAM 
MÔN TOÁN ( thời gian: 90 phút )
Câu 1: Cho hàm số . Chọn phát biểu đúng
	A. 	B. 	C. 	D. 
Câu 2: Tìm tiệm cận ngang của đồ thị hàm số .
	A. 	B. 	C. 	D. 
Câu 3: Tính diện tích hình phẳng được đánh dấu trên hình bên
	A. 	B. 	C. 	D. 
Câu 6: Cho hàm số liên tục trên với bảng xét dấu đạo hàm như sau:
x
 1 2 
f ’(x)
 0 0 + 0 +
Hãy cho biết hàm số có bao nhiêu điểm cực trị
	A. 0	B. 2	C. 3	D. 1
Câu 7: Gọi m là giá trị nhỏ nhất của hàm số . Tìm m.
	A. 	B. 	C. 	D. 
Câu 8: Một hình trụ có 2 đáy là 2 hình tròn tâm O và O’ và có bán kính . Khoảng cách giữa 2 đáy là . Gọi là mặt phẳng qua trung điểm của đoạn OO’ và tạo với đường thẳng OO’ một góc 450. Tính diện tích S của thiết diện tạo bởi mặt phẳng và hình trụ.
	A. 	B. 	C. 	D. 
Câu 9: Cho hình chóp S.ABC. Gọi M là trung điểm của SA và N là điểm trên SC sao cho . Tính tỷ số k giữa thể tích khối chóp ABMN và thể tích khối chóp S.ABC.
	A. 	B. 	C. 	D. 
Câu 10: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu tâm tiếp xúc với Oz.
	A. 	B. 
	C. 	D. 
Câu 11: Đồ thị hình bên là đồ thị của hàm số nào?
	A. 	B. 	C. 	D. 
Câu 14: Tìm nguyên hàm của hàm số 
	A. 	B. 
	C. 	D. 
Câu 15: Gọi r;h;l lần lượt là bán kính đáy , chiều cao và đường sinh của khối nón lần lượt là diện tích xung quanh , diện tích toàn phần hình nón và thể tích khối nón. Chọn phát biểu sai.
	A. 	B. 	C. 	D. 
Câu 16: Cho khối cầu (O) bán kính , mặt phẳng cách tâm O của khối cầu một khoảng bằng 1, cắt khối cầu theo một hình tròn. Gọi S là diện tích của hình tròn này. Tính S.
	A. 	B. 	C. 	D. 
Câu 17: Cho hàm số . Tọa độ điểm cực tiểu của đồ thị hàm số là
	A. 	B. 	C. 	D. 
Câu 18: Trong không gian toạ độ Oxyz cho . Viết phương trình trung trực của của đoạn AB biết nằm trong mặt phẳng 
	A. 	B. 	C. 	D. 
Câu 21: Tìm a để 
	A. 	B. 	C. 	D. 
Câu 22: Cho hàm số liên tục trên . Biết , hãy tính 
	A. 	B. 	C. 	D. 
Câu 23: Trong không gian với hệ tọa độ Oxyz, cho . Tính khoảng cách từ điểm O đến mặt phẳng (ABC).
	A. 	B. 	C. 	D. 
Câu 24: Trong không gian toạ độ Oxyz, cho đường thẳng và mặt phẳng . Gọi là góc giữa đường thẳng và mặt phẳng (P). Số đo góc gần nhất với giá trị nào dưới đây.
	A. 	B. 	C. 	D. 
Câu 25: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh SA vuông góc với mặt đáy (ABC) và . Tính thể tích khối chóp S.ABC.
	A. 	B. 	C. 	D. 
Câu 26: Biết và . Tính theo a và b.
	A. 	B. 	C. 	D. 
Câu 27: Từ một miếng tôn cạnh bằng 8dm, người ta cắt ra một hình quạt tâm O bán kính ( xem hình ). Để cuộn lại thành một chiếc phễu hình nón (khi đó OA trùng với OB ). Chiều cao chiếc phễu đó có số đo gần đúng ( làm tròn đến 3 chữ số thập phân) là: 
	A. 7, 748 dm	B. 7, 747 dm
	C. 7, 745 dm	D. 7, 746 dm
Câu 28: Bất phương trình có nghiệm là
	A. 	B. 	C. 	D. 
Câu 31: Phương trình có nghiệm là 
	A. 	B. 	C. 	D. 
Câu 32: Độ dài đường chéo của một hình lập phương 6a. Tính thể tích V của khối lập phương.
	A. 	B. 	C. 	D. 
Câu 35: Cho các hàm số . Chọn phát biểu sai
	A. Có hai đồ thị có tiệm cận đứng.	B. Có hai đồ thị có tiệm cận ngang.
	C. Có đúng hai đồ thị có tiệm cận.	D. Có hai đồ thị có chung một đường tiệm cận.
Câu 36: Biết . Tính giá trị biểu thức 
Câu 40: Cho các đẳng thức thức sau
	A. Có ba đẳng thức đúng.	B. Có hai đẳng thức đúng. 
	C. Có một đẳng thức đúng. 	D. Không có đẳng thức nào đúng. 
Câu 41: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng . Xác định m biết .
	A. 	B. 	C. 	D. 
Câu 42: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu . Tìm tọa độ điểm M thuộc mặt cầu (S) sao cho khoảng cách từ M đến trục Ox là lớn nhất.
	A. 	B. 	C. 	D. 
Câu 43: Xác định a sao cho .
	A. 	B. 	C. 	D. 
Câu 46: Cho biểu thức . Xác định k sao cho biểu thức .
	A. 	B. 	C. 	D. Không tồn tại k.
Câu 47: Xét các hàm số được nêu trong các phương án A, B, C, D dưới đây. Hàm số nào không đồng biến trên từng khoảng xác định của nó?
	A. 	B. 	
	C. 	D. 
Câu 50: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng . Xác định vị trí tương đối của d và .
	A. 	B. 	C. (d) cắt 	D. 
Đáp án
1-A
2-B
3-C
4-A
5-C
6-D
7-B
10-D
11-D
12-B
15-A
16-A
17-D
20-A
21-A
22-D
25-C
26-A
27-D
30-D
31-D
32-B
39-C
40-B
41-A
42-D
43-C
44-C
49-D
50-D
LỜI GIẢI CHI TIẾT
Câu 1: Đáp án A
Ta có: 
Câu 2: Đáp án B
Ta có: => Đồ thị hàm số có tiệm cận ngang .
Câu 3: Đáp án C
Do . Do trong hình vẽ ta tính phần đồ thị với do đó tính diện tích hình phẳng cần tính là diện tích hình phẳng giới hạn bởi các đường , . Khi đó .
Câu 6: Đáp án D
Dựa vào bảng xét dấu ta thấy đổi dấu qua điểm suy ra hàm số có một cực trị tại .
Câu 7: Đáp án B
Hàm số xác định khi và chỉ khi 
Ta có 
Suy ra 
Câu 8: Đáp án B
Gọi H là trung điểm của CD khi đó 
Khi đó 
Suy ra . Mặt khác 
Do đó diện tích thiết diện là 
Câu 9: Đáp án B
Ta có: 
Do đó 
Lại có: 
Khi đó 
+) Đồ thị hàm số đi qua các điểm có tọa độ Loại A, C
Câu 12: Đáp án B
Ta có: 
Suy ra hàm số đồng biến trên khoảng , nghịch biến trên khoảng 
Câu 13: Đáp án A
Thể tích cần tính bằng 
Câu 14: Đáp án B
Ta có 
Câu 15: Đáp án A
Ta có: A sai
Câu 16: Đáp án A
Bán kính đáy của hình tròn bằng:
Câu 17: Đáp án D
Ta có 
Mặt khác Tọa độ điểm cực tiểu của đồ thị hàm số là 
Câu 18: Đáp án B
Trung điểm của AB là .
Ta có: . Khi đó 
Câu 21: Đáp án A
Ta có: 
Câu 22: Đáp án D
Đặt 
Câu 23: Đáp án D
Phương trình mặt phẳng (ABC) theo đoạn chắc là: hay 
Do đó: 
Câu 24: Đáp án D
Ta có: và . Khi đó: 
Do đó: 
Câu 25: Đáp án C
Ta có: 
Câu 26: Đáp án A
Ta có 
Câu 27: Đáp án D
Chu vi của đáy hình nón có độ dài bằng cung AB.
Độ dài cung AB là: . Suy ra bán kính đường tròn đáy hình nón là: 
Độ dài đường sinh của hình nón là 
Câu 28: Đáp án C
Câu 29: Đáp án C
Do MNPQ là hình bình hành nên 
Câu 30: Đáp án D
Ta có: 
Câu 31: Đáp án D
Câu 32: Đáp án B
Đặt khi đó độ dài đường chéo của khối lập phương 
Câu 33: Đáp án B
Giả sử là nghiệm của PT đã cho thì cũng là nghiệm của PT. khi đó để phương trình đã cho có một nghiệm duy nhất thì 
Với hệ này có 3 nghiệm phân biệt.
Do đó không tồn tại giá trị của m thỏa mãn yêu cầu bài toán.
Câu 34: Đáp án C
Gọi H là trung điểm cạnh CD của khối chóp tứ giác đều S.ABCD. 
Khi đó suy ra 
Ta có: 
. Mặt khác 
Khi đó 
Câu 35: Đáp án C
Dựa vào đáp án ta thấy
Đồ thị hai hàm số cùng có tiệm cận đứng là đường thẳng 
Đồ thị hai hàm số cùng có tiệm cận ngang là: 
Có 3 đồ thị hàm số có tiệm cận nên C sai.
Câu 36: Đáp án A
Ta có: 
Câu 37: Đáp án A
Cho , ta có : 
Khi đó dễ nhận thấy 
Câu 38: Đáp án C
Hình bát diện đều có 9 mặt phẳng đối xứng.
Câu 39: Đáp án C
Ta có: . Hàm số đạt cực trị tại khi pt có nghiệm và đó không phải nghiệm kép. Khi đó không tồn tại m thỏa mãn yêu cầu đề bài.
Câu 40: Đáp án B
Chú ý hàm số xác định khi và hàm số xác định khi 
Ta có: do đó có 2 đẳng thức đúng.
Câu 41: Đáp án A
Ta có: . Để thì 
Chú ý: Với mặt phẳng này chứa Ox vì khi đó 
Câu 42: Đáp án D
Cách 1: Thử từng đáp án ta thấy là điểm thỏa mãn yêu cầu.
Cách 2: có tâm suy ra hình chiếu vuông góc của I trên Ox là . Cho suy ra là điểm thỏa mãn.
Câu 43: Đáp án C
Câu 44: Đáp án C
Câu 45: Đáp án C
Ta có: 
Câu 46: Đáp án A
Ta có: 
Câu 47: Đáp án B
Dựa vào đáp án ta thấy
+) Hàm số có tập xác định hàm số đồng biến trên tập xác định.
+) Hàm số có tập xác định hàm số không đồng biến trên tập xác định.
+) Hàm số có tập xác định hàm số đồng biến trên tập xác định.
+) Hàm số có tập xác định => Hàm số đồng biến trên tập xác định.
Câu 48: Đáp án A
Phương trình mặt phẳng qua M và vuông góc với là: 
Khi đó 
Câu 49: Đáp án D
Ta có: 
Suy ra ta có : 
Do đó: 
Câu 50: Đáp án D
Ta có: , mặt khác điểm nhưng không thuộc nên .