Đề thi kiểm định học sinh giỏi Toán 7 lần 1 năm học 2016 – 2017

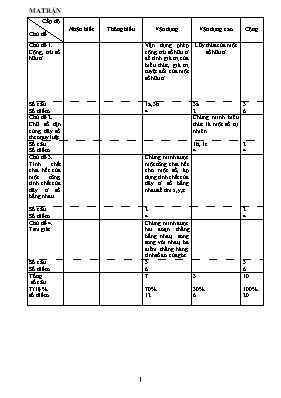
MA TRẬN
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
Cộng
Chủ đề 1. 
Cộng, trừ số hữu tỉ 
Vận dụng phép cộng, trừ số hữu tỉ để tính giá trị của biểu thức, giá trị tuyệt đối của một số hữu tỉ
Lũy thừa của một số hữu tỉ
Số câu 
Số điểm 
1a, 3b
4
3a
2
3
6
Chủ đề 2. 
Chữ số tận cùng, dãy số theo quy luật
Chứng minh biểu thức là một số tự nhiên
Số câu 
Số điểm
1b, 1c
4
2
4
Chủ đề 3. 
Tính chất chia hết của một tổng, tính chất của dãy tỉ số bằng nhau
Chứng minh được một tổng chia hết cho một số, áp dụng tính chất của dãy tỉ số bằng nhau để tìm x,y,z
Số câu 
Số điểm 
2
4
2
4
Chủ đề 4. 
Tam giác 
Chứng minh được hai đoạn thẳng bằng nhau, song song với nhau, ba điểm thẳng hàng, tính số đo của góc 
Số câu 
Số điểm 
3
6
3
6
Tổng
 số câu 
Tỉ lệ %
số điểm
7
70%
12
3
30%
6
10
100%
20
PHÒNG GD&ĐT TÂN KỲ
TRƯỜNG THCS HƯƠNG SƠN
ĐỀ THI KIỂM ĐỊNH HSG TOÁN 7 LẦN 1
NĂM HỌC 2016 – 2017
Thời gian làm bài: 150 phút
Câu 1(6 điểm). 
a) Thực hiện phép tính. 
b) Cho . Chứng tỏ rằng A là một số tự nhiên.
c) Tính tổng.
Câu 2( 2 điểm). 
 Chứng minh rằng chia hết cho 211.
Câu 3( 6,0 điểm). 
Tìm x biết 
Tìm x biết 
Tìm các số x,y,z biết rằng và x – y = 15 . 
Câu 6( 6 điểm). Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) AC = EB và AC // BE
b) Gọi I là một điểm trên AC ; K là một điểm trên EB sao cho AI = EK . Chứng minh ba điểm I , M , K thẳng hàng
c) Từ E kẻ . Biết ; .
Tính và 
----Hết-----
HƯỚNG DẪN CHẤM HSG TOÁN 7 lần 1
Câu
Ý
Nội dung
Điểm
1
a
2
b
 ta có
== 10.B
A= 0,9.10.B = 9 .B mà 
1
0,5
0,5
c
0,5
0,5
0,5
0,5
2
2 điểm
Chứng minh rằng chia hết cho 211
Ta có = 
Mà 211 chia hết 211 Vậy 
0,1
0,5
0,5
3
a
1
1
b
Tìm x biết 
a)2x-3 = x-1 => x = 2 ( TM )
b)2x-3 = 1 – x => x = 4/3 ( TM )
Vậy với x = 2 hoặc x = 4/3 thì 
0,5
0,5
0,5
0,5
c
Tìm các số x,y,z biết rằng và x – y = 15
 và x – y = 15
Vậy x,y,z lần lượt là 60, 45, 40
0,5
0,5
0,5
0,5
6
a
 Xét và có :AM = EM (gt )AMC = EMB (đối đỉnh ) BM = MC (gt )
Nên : = (c.g.c )	0,5 điểm AC = EB	
Vì = MAC = MEB
(2 góc có vị trí so le trong được tạo bởi đường thẳng AC và EB cắt đường thẳng AE ) 
Suy ra AC // BE . 
0,5
0,5
0,5
0,5
b
Xét và có : AM = EM (gt )MAI = MEK ( vì ) AI = EK (gt )Nên ( c.g.c ) 	
Suy ra: AMI = EMK Mà AMI + IME = 180o ( tính chất hai góc kề bù )
 EMK + IME = 180o Ba điểm I;M;K thẳng hàng
1
0,5
0,5
c
Trong tam giác vuông BHE ( H = 90o ) có HBE = 50o HEB = 90o - HBE = 90o - 50o = 40o HEM = HEB - MEB = 40o - 25o = 15o BME là góc ngoài tại đỉnh M của Nên BME = HEM + MHE = 15o + 90o = 105o 
 ( định lý góc ngoài của tam giác ) 
1
0,5
0,5
( Học sinh giải theo cách khác đúng kết quả vẫn cho điểm tối đa)