Đề thi học sinh giỏi thành phố Tin học (Đề chính thức) - Năm học 2016-2017 - Sở GD & ĐT Hải Phòng

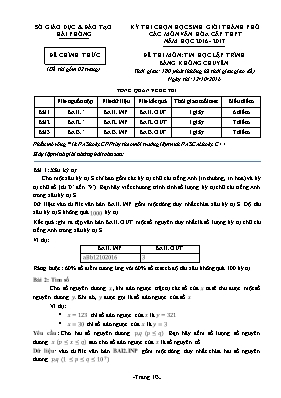
SỞ GIÁO DỤC & ĐÀO TẠO
HẢI PHÒNG
ĐỀ CHÍNH THỨC
(Đề thi gồm 02 trang)
KỲ THI CHỌN HỌC SINH GIỎI THÀNH PHỐ
 CÁC MÔN VĂN HÓA CẤP THPT 
NĂM HỌC 2016 - 2017
ĐỀ THI MÔN: TIN HỌC LẬP TRÌNH
BẢNG KHÔNG CHUYÊN
Thời gian: 180 phút (không kể thời gian giao đề)
Ngày thi: 12/10/2016
TỔNG QUAN VỀ ĐỀ THI
File nguồn nộp
File dữ liệu
File kết quả
Thời gian mỗi test
Biểu điểm
Bài 1
BAI1.*
BAI1.INP
BAI1.OUT
1 giây
6 điểm
Bài 2
BAI2.*
BAI2.INP
BAI2.OUT
1 giây
7 điểm
Bài 3
BAI3.*
BAI3.INP
BAI3.OUT
1 giây
7 điểm
Phần mở rộng * là PAS hoặc CPP tùy theo môi trường lập trình PASCAL hoặc C++
Hãy lập trình giải những bài toán sau:
Bài 1: Xâu ký tự
Cho một xâu ký tự S chỉ bao gồm các ký tự chữ cái tiếng Anh (in thường, in hoa) và ký tự chữ số (từ ‘0’ đến ‘9’). Bạn hãy viết chương trình tính số lượng ký tự chữ cái tiếng Anh trong xâu ký tự S.
Dữ liệu: vào từ file văn bản BAI1.INP gồm một dòng duy nhất chứa xâu ký tự S. Độ dài xâu ký tự S không quá 1000 ký tự.
Kết quả: ghi ra tệp văn bản BAI1.OUT một số nguyên duy nhất là số lượng ký tự chữ cái tiếng Anh trong xâu ký tự S.
Ví dụ:
BAI1.INP
BAI1.OUT
aBb12102016
3
Ràng buộc: 60% số điểm tương ứng với 60% số test có độ dài xâu không quá 100 ký tự. 
Bài 2: Tìm số
Cho số nguyên dương x, khi đảo ngược trật tự các số của x ta sẽ thu được một số nguyên dương y. Khi đó, y được gọi là số đảo ngược của số x.
Ví dụ:
x=123 thì số đảo ngược của x là y=321
x=30 thì số đảo ngược của x là y=3
Yêu cầu: Cho hai số nguyên dương p,q (p≤q). Bạn hãy đếm số lượng số nguyên dương x (p≤x≤q) sao cho số đảo ngược của x là số nguyên tố.
Dữ liệu: vào từ file văn bản BAI2.INP gồm một dòng duy nhất chứa hai số nguyên dương p,q (1≤p≤q≤107)
Kết quả: ghi ra file văn bản BAI2.OUT một số nguyên duy nhất là số lượng số nguyên dương x (p≤x≤q) mà số đảo ngược của x là số nguyên tố.
Ví dụ:
BAI2.INP
BAI2.OUT
Giải thích
10 13
2
x=10→y=1, y không là số nguyên tố
x=11→y=11, y là số nguyên tố
x=12→y=21, y không là số nguyên tố
x=13→y=31, y là số nguyên tố
Ràng buộc: 60% số test tương ứng với 60% số điểm có q-p≤1000.
Bài 3: Cặp số chia hết cho 3
Với hai số nguyên dương u,v, khi viết số v sau số u ta được một số mới.
Ví dụ: u=99,v=123, khi viết số v sau số u, ta được số mới là số 99123
Cho n số nguyên dương a1,a2,,an và m số nguyên dương b1,b2,,bm. Với mỗi giá trị bi (1≤i≤m), bạn hãy cho biết có bao nhiêu số aj(1≤j≤n) sao cho khi viết aj sau bi được một số mới chia hết cho 3?
Dữ liệu: vào từ file văn bản BAI3.INP
Dòng đầu chứa hai số nguyên dương n,m (1≤n,m≤100000)
Dòng tiếp theo chứa n số nguyên dương a1,a2,,an (ai≤108, 1≤i≤n) 
Dòng tiếp theo chứa m số nguyên dương b1,b2,,bm(bi≤108, 1≤i≤m).
Kết quả: ghi ra file văn bản BAI3.OUT trên m dòng, dòng thứ i ghi số lượng số aj(1≤j≤n) sao cho khi viết aj sau bi được một số mới chia hết cho 3.
Ví dụ:
BAI3.INP
BAI3.OUT
Giải thích
5 2
123 4 5 7 10
3 2
1
3
b1=3, có duy nhất một số a1 khi viết sau b1 tạo thành các số 3123 chia hết cho 3.
b2=2, có ba số a2,a4,a5 khi viết sau b2 tạo thành các số 24, 27, 210 chia hết cho 3.
Ràng buộc: 60% số test tương ứng với 60% số điểm có 1≤n,m≤1000.
Chú ý:
- Bài thi được làm trên máy vi tính.
- Học sinh đặt tên file chương trình theo đúng quy định của từng bài, không ghi bất kỳ thông tin cá nhân nào vào file bài làm (họ tên, số báo danh, ngày sinh, trường, các ký hiệu khác thường,)
- File dữ liệu vào và kết quả ra ở trong thư mục hiện hành, thí sinh không phải khai báo đường dẫn đến các file này.
---Hết---
(Thí sinh không sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh:	Số báo danh:	
Giám thị 1:	Giám thị 2: