Đề thi học kì II môn: Toán (khối 11)

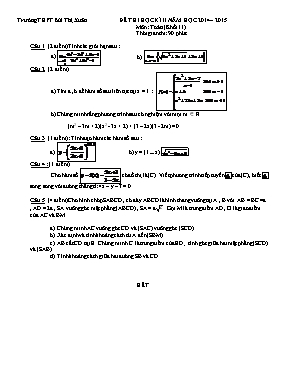
Trường THPT Bùi Thị Xuân	ĐỀ THI HỌC KÌ II NĂM HỌC 2014 – 2015
	Môn: Toán (Khối 11)
	Thời gian thi: 90 phút
Câu 1. (2 điểm) Tính các giới hạn sau :
	a) 	 b) 
Câu 2. (2 điểm) 
	a) Tìm a , b để hàm số sau liên tục tại x = 1 : 
	b) Chứng minh rằng phương trình sau có nghiệm với mọi m ∈ R
 	(m2 – 3m + 2)(x2 - 3x + 2) + (3 – 2x)(3 - 2m) = 0 
Câu 3. (1 điểm) : Tính đạo hàm các hàm số sau : 
 	 b) y = (1 - x).
Câu 4 : (1 điểm) 
	Cho hàm số có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết song song với đường thẳng d: 4x – y – 7 = 0. 
Câu 5. (4 điểm) Cho hình chóp SABCD , có đáy ABCD là hình thang vuông tại A , B với AB = BC =a , AD = 2a , SA vuông góc mặt phẳng (ABCD) , SA = a2 . Gọi M là trung điểm AD , O là giao điểm của AC và BM
Chứng minh AC vuông góc CD và (SAC) vuông góc (SCD).
Xác định và tính khoảng cách từ A đến (SBM).
AB cắt CD tại E . Chứng minh C là trung điểm của ED ; tính góc giữa hai mặt phẳng (SCD) và (SAB).
Tính khoảng cách giữa hai đường SB và CD.
HẾT
ĐÁP ÁN – THANG ĐIỂM 
ĐỀ THI HỌC KỲ II NĂM HỌC 2014 – 2015 TOÁN 11
(đáp án gồm 4 trang )
Đáp án
Điểm
Câu 1. (2 điểm) Tính các giới hạn
a) b) 
b) = 
 = 
= 
0,25+0,25
0,25
0,25
0,25
0,25
0,25
0,25
2. a) Ta có f(1) = a + b ; 
Hàm số liên tục tại x = 1 ⟺ 
b) Cách 1: Đặt thì f(x) là hàm số xác định và liên tục trên R 
Ta có: f(1) = –(3–2m) và f(2) = 3 – 2m
 f(1).f(2) = –(3 – 2m)2 ≤ 0 với mọi (2)
+ Xét 3 – 2m = 0 
Phương trình f(x) = 0 có ít nhất 2 nghiệm là x = 1 v x = 2
 + Xét 
 Phương trình f(x) = 0 có ít nhất 1 nghiệm trên (1; 2)
Vậy, trong cả hai trường hợp thì pt f(x) = 0 luôn có nghiệm với mọi 
Cách 2: Đặt thì f(x) là hàm số xác định và liên tục trên R (1)
Ta có: f(1) = –(3–2m) và f(2) = 3 – 2m
 f(1).f(2) = –(3 – 2m)2 ≤ 0 với mọi (2)
Từ (1) và (2) suy ra phương trình f(x) = 0 có nghiệm xo ∈ [1;2] với mọi m ∈ R 
Chú ý: nếu HS ghi kết luận có nghiệm trên (1; 2) mà không làm tiếp thì trừ 0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
3. a) 
b) 
Chú ý: HS không rút gọn thì cũng tha
0,25
0,25
0,25
0,25
Câu 4.
Gọi là tiếp điểm và là hệ số góc của tiếp tuyến 
, hay . Suy ra d có hệ số góc 
 song song với d 
Ta có: 
Ta có: 
+ Với 
Phương trình tiếp tuyến tại 
hay (nhận)
+ Với 
Phương trình tiếp tuyến tại 
hay (loại vì trùng với d)
Vậy, 
Chú ý: Nếu học sinh không loại một trường hợp của thì trừ 0,25đ
0,25
0,25
0,25
0,25
Câu 5. (4 điểm) 
a) Ta có: Tứ giác ABCM là hình vuông
⟹ . Suy ra, Tam giác ACD vuông tại C, hay CD⊥ AC
 Ta có: 
Mà: 
⟹ (SCD) ⊥ (SAC)
Chú ý: nếu HS chỉ nhận nhanh ABCM là hình vuông thì cũng được 0,25đ
0,25
0,25
0,25
0,25
b) Trong (SAC), kẻ tại H
Ta có MD//BC và MD = BC = a nên tứ giác BCDM là hình bình hành. Suy ra: BM //CD
Ta có: 
 tại H 
Ta có: 
Tam giác SAO vuông tại O có AH là đường cao nên: 
Vậy, 
0,25
0,25
0,25
0,25
c) Ta có BC //AD và 2BC = 2a = AD nên BC là đường trung bình của tam giác EAD, suy ra C là trung điểm của ED.
Trong (SAB), kẻ kẻ tại F (1)
Ta có: 
Mà: 
(1),(2),(3) 
Ta có: 
(do nên . Suy ra tam giác ADF vuông tại A nên )
Tam giác SAE có 
Ta có: 
Vậy góc giữa hai mặt phẳng (SCD) và (SAB) bằng 60o. 
0,25
0,25
0,25
0,25
d) Ta có: 
⟹ d(CD, SB) = d(CD,(SBM)) = d(D, (SBM)) 
⟹ d(CD, SB) = d(A, (SBM)) = (cmt)
0,25
0,25
0,25
0,25