Đề thi học kì I năm học 2014-2015 môn Toán lớp 9

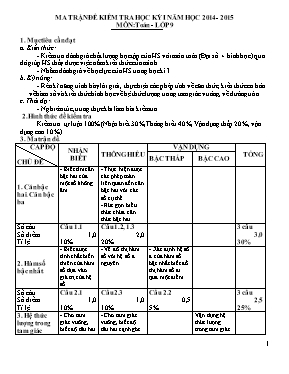
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2014 - 2015
MÔN:Toán - LỚP 9
1. Mục tiêu cần đạt
a. Kiến thức: 
	- Kiểm tra đánh giá chất lượng học tập của HS với môn toán (Đại số + hình học) qua đó giúp HS thấy được việc nắm kiến thức của mình
	- Nhằm đánh giá về học lực của HS trong học kì I.
b. Kỹ năng: 
	- Rèn kĩ năng trình bày lời giải, thực hiện các phép tính về căn thức, kiến thức cơ bản về hàm số và kiến thức hình học về hệ thức lượng trong tam giác vuông, về đường tròn.
c. Thái độ:
	- Nghiêm túc, trung thực khi làm bài kiểm tra
 2. Hình thức đề kiểm tra
	Kiểm tra tự luận 100% (Nhận biết 30%; Thông hiểu 40%, Vận dụng thấp 20 %, vận dụng cao 10%).
3. Ma trận đề.
CẤP ĐỘ
CHỦ ĐỀ
NHẬN BIẾT
THÔNG HIỂU
VẬN DỤNG
TỔNG
BẬC THẤP
BẬC CAO
1. Căn bậc hai. Căn bậc ba
- Biết tìm căn bậc hai của một số không âm.
- Thực hiện được các phép toán liên quan đến căn bậc hai với các số cụ thể.
- Rút gọn biểu thức chứa căn thức bậc hai.
Số câu
Số điểm
Tỉ lệ
Câu 1.1
1,0
10%
Câu 1.2, 1.3
2,0
20%
3 câu
3,0
30%
2. Hàm số bậc nhất.
- Biết được tính chất biến thiên của hàm số dựa vào giá trị của hệ số 
- Vẽ đồ thị hàm số với hệ số a nguyên.
- Xác định hệ số a của hàm số bậc nhất biết đồ thị hàm số đi qua một điểm.
Số câu 
Số điểm
Tỉ lệ
Câu 2.1
1,0
10%
Câu 2.3
1,0
10%
Câu 2.2
0,5
5%
3 câu
2,5
25%
3. Hệ thức lượng trong tam giác vuông.
- Cho tam giác vuông, biết độ dài hai cạnh góc vuông:
+ Viết được tan của một góc nhọn. 
- Cho tam giác vuông, biết độ dài hai cạnh góc vuông:
+ Tìm độ dài đường cao trong tam giác vuông.
Vận dụng hệ thức lượng trong tam giác vuông giải bài toán thực tế.
Số câu
Số điểm
Tỉ lệ
Câu 3.1
0,5
5%
Câu 3.2
1,0
10%
Câu 5
1,0
10%
3 câu
2,5
25%
4. Đường tròn
+ Vẽ hình minh họa. Ghi GT, KL
-Vận dụng tính chất quan hệ phân giác của góc tạo bởi hai tiếp tuyến,
-Vận dụng được định nghĩa đường trung bình của tam giác.
Số câu
Số điểm
Tỉ lệ
0,5
 5%
Câu 4.1, 4.2
1,5
15%
2 câu
2,0
20%
Tổng số câu
Tổng số điểm
Tỉ lệ 100%
3 câu
3,0 đ
30%
4 câu
4,0 đ
40%
3 câu
2,0 đ
20%
1 câu
1,0 đ
10%
11 câu
10đ
100%
ĐỀ THI HỌC KÌ I NĂM HỌC 2014-2015
Điểm
MÔN TOÁN LỚP 9:
THỜI GIAN:
Họ và tên:
Trường:..
ĐỀ BÀI
Câu 1.(3đ)
	a.Tính . 
	b. Tính: 
	c. Rút gọn biểu thức.
Câu 2. (2,5đ) Cho hàm số y = 2x + 3 
	a. Hàm số trên đồng biến hay nghịch biến. 
	b. Vẽ đồ thị của hàm số trên. 
	c. Cho hàm số y = ax+3. Tìm hệ số a nếu biết hàm số đi qua điểm A(1,4). 
Câu 3 (2,5đ). Cho hình vẽ sau đây
a.Viết tang của góc 	
b.Tính độ dài AH. 
c.Trong một buổi cắm trại có một sợi dây chiều dài 14 mét, một bạn được yêu cầu dựng cột chống sao cho chia sợi dây đó thành hai phần có chiều dài là 6 mét và 8 mét, hỏi chân cột phải đặt tại vị trí nào trên đường nối hai đầu sợi dây cọc để cọc vuông góc với mặt đất. 
Câu 4. (2đ) cho đường tròn (O,R) và hai tiếp tuyến của đường tròn là AB,AC cắt nhau tại A AO cắt BC tại H.
a.Chứng minh rằng H là trung điểm của BC
b.Đường kéo dài của bán kính CO cắt đường tròn tại D chứng minh rằng BD song song với AO
ĐÁP ÁN VÀ BIỂU ĐIỂM
Câu 1.
	a.Tính = 2. 1đ
	b. Tính: 1đ
	c. Rút gọn biểu thức.
 1đ
Câu 2. Cho hàm số y = 2x + 3 
	a. Hàm số trên đồng biến vì hệ số a = 2>0. 1đ
	b. Vẽ đồ thị của hàm số trên. 1đ
1
O
3
2
1
-2
 -1
-2
2
y = 2x + 3
y
 x
-1,5
	c. Cho hàm số y = ax+3. Vì hàm số đã cho đi qua điểm A(1,4) nên ta có:
 4 = a.1+3 a = 1. 0,5đ
Câu 3 Cho hình vẽ sau đây
a.tanC = 	0,5đ
b .áp dụng định lí pitago cho tam giác vuông ∆ACH 
Do AH.BC = AC.AB 1đ
c. Theo hình vẽ trên. Nếu một đầu cọc được đặt vào vị trí chia sợi dây ra làm hai phần bằng 6m, một phần bằng 8m. ta gọi đầu cọc đó là A, đoạn AC = 6m, đoạn BC = 8m. vị trí điểm H cách C một đoạn sau đây thì cọc sẽ vuông góc với mặt đất.
 1đ
Câu 4. 	 
GT
C
B
A
H
O
D
1
Cho đường tròn(O,R) có hai tiếp tuyến AB,AC cắt nhau tại A. AO cắt BC tại H
KL
a.H là trung điểm BC.
b.Đường kéo dài của bán kính CO cắt đường tròn tại D chứng minh rằng BD song song với AO.
0,5đ
 	 Giải
a. Có AB = AC (t/c tiếp tuyến)
	OB = OC = R
	Þ OA là trung trực của BC
	Þ OA ^ BC và HB = HC 0,75đ
b. Xét DCBD có:
	 là đường trung bình của DCBD
	Þ BD // OH hay OA // BD 0,75đ