Đề thi chọn học sinh giỏi Toán 9 thi ngày 05 - 12 - 2015

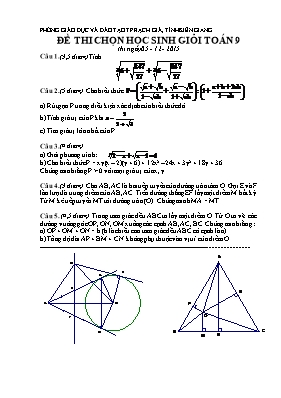
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO TP RẠCH GIÁ, TÌNH KIÊN GIANG
ĐỀ THI CHỌN HỌC SINH GIỎI TOÁN 9
thi ngày 05 - 12 - 2015
Câu 1. (3,5 điểm) Tính 
Câu 2. (5 điểm) Cho biểu thức 
a) Rút gọn P trong điều kiện xác định của biểu thức đó.
b) Tính giá trị của P khi 
c) Tìm giá trị lớn nhất của P.
Câu 3. (4 điểm) 
a) Giải phương trình: 
b) Cho biểu thức P = xy(x 2)(y + 6) + 12x2 24x + 3y2 + 18y + 36
Chứng minh rằng P > 0 với mọi giá trị của x, y.
Câu 4. (3 điểm) Cho AB, AC là hai tiếp tuyến của đường tròn tâm O. Gọi E và F lần lượt là trung điểm của AB, AC. Trên đường thẳng EF lấy một điểm M bất kỳ. Từ M kẻ tiếp tuyến MT tới đường tròn (O). Chứng minh MA = MT.
Câu 5. (4,5 điểm) Trong tam giác đều ABC ta lấy một điểm O. Từ O ta vẽ các đường vuông góc OP, ON, OM xuống các cạnh AB, AC, BC. Chứng minh rằng:
a) OP + OM + ON = h (h là chiều cao tam giác đều ABC có cạnh là a).
b) Tổng độ dài AP + BM + CN không phụ thuộc vào vị trí của điểm O. 
--------------------------------------------------------------------------------------------------