Đề thi chọn học sinh giỏi giải Toán trên máy tính cầm tay năm học 2011 - 2012 môn: Toán lớp 9

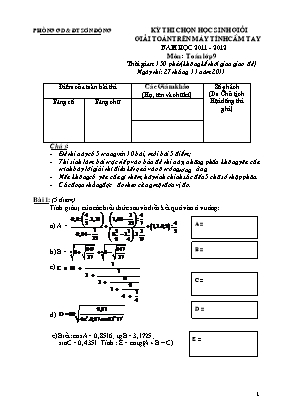
phßng Gd & ®t S¬n ®éng	 kú thi chän häc sinh giái 
gi¶i to¸n trªn m¸y tÝnh cÇm tay
	 n¨m häc 2011 - 2012
 M«n : To¸n líp 9 
 Thêi gian: 150 phót (kh«ng kÓ thêi gian giao ®Ò)
 Ngµy thi: 27 th¸ng 11 n¨m 2011	
§iÓm cña toµn bµi thi
C¸c Gi¸m kh¶o
(Hä, tªn vµ ch÷ kÝ)
Sè ph¸ch
(Do Chñ tÞch Héi ®ång thi ghi)
B»ng sè
B»ng ch÷
Chó ý: 
§Ò thi nµy cã 5 trang với 10 bµi, mçi bµi 5 ®iÓm;
ThÝ sinh lµm bµi trùc tiÕp vµo b¶n ®Ò thi nµy, nh÷ng phÇn kh«ng yªu cÇu tr×nh bµy lêi gi¶i th× ®iÒn kÕt qu¶ vµo « trèng t­¬ng øng. 
NÕu kh«ng cã yªu cÇu g× thªm, h·y tÝnh chÝnh x¸c ®Õn 5 ch÷ sè thËp ph©n. 
C¸c ®o¹n th¼ng ®­îc ®o theo cïng mét ®¬n vÞ ®o.
Bài 1: (5 điểm)
Tính giá trị của các biểu thức sau và điền kết quả vào ô vuông:
A = 
B = 
 	a) A = 	 KQ: 
 b) B = 
D = 
C = 
c) 
d) 
E = 
 e) Biết: cosA = 0,8516 ; tgB = 3,1725 ; 
 sinC = 0,4351. Tính : E = cotg(A + B – C) 
Bài 2: (5 điểm)
Tìm giá trị của x, y dưới dạng phân số (hoặc hỗn số) từ các phương trình sau rồi điền kết quả vào ô vuông :
x =
 a) 
y = 
b) 
Bài 3: (5 điểm)
b = 
a = 
a) Tìm các số tự nhiên a và b biết rằng	
b) T×m sè tù nhiªn lín nhÊt, nhá nhÊt (t­¬ng øng ®Æt lµ a, b) cã d¹ng chia hÕt cho 7
Bµi 4:(5®iÓm) 
a) Mét ng­êi göi a ®ång vµo ng©n hµng víi l·i suÊt tiÕt kiÖm lµ r%/th¸ng. BiÕt r»ng hµng th¸ng ng­êi ®ã kh«ng rót l·i suÊt ra. H·y lËp c«ng thøc tÝnh sè tiÒn c¶ gèc vµ l·i cña ng­êi ®ã sau 1 th¸ng, 2 th¸ng , 3 th¸ng , 1 n¨m theo a vµ r? ¸p dông víi a = 1 triÖu ®ång vµ r = 0,4
¸p dông víi a= 1 triÖu ®ång, r =0,4. Tæng sè tiÒn c¶ gèc vµ l·i cña ng­êi ®ã sau 1 th¸ng, 2 th¸ng , 3 th¸ng , 1 n¨m lµ:
Sau 1 th¸ng
Sau 2 th¸ng
Sau 3 th¸ng
Sau 1 n¨m
Tæng sè tiÒn
b) NÕu cø mçi th¸ng ng­êi ®ã göi vµo ng©n hµng 1 triÖu ®ång vµ l·i xuÊt vÉn lµ 0,4% (c¸c th¸ng còng kh«ng rót l·i suÊt ra) th× sau mét n¨m ng­êi ®ã cã ®­îc bao nhiªu tiÒn ?
Bài 5: (5 điểm )
Cho U0 = 2; U1 = 3; Un + 1 = 3Un - 2Un - 1 ( n Î N* ) 
ViÕt quy tr×nh bÊm phÝm liªn tôc tÝnh Un ( n ≥ 3 ).
...............................................Sö dông quy tr×nh hoµn thµnh b¶ng sau:
n
2
3
4
5
6
7
8
9
10
Un
5
9
17
33
65
129
257
513
1025
b) Chøng minh U2n + Un + 1 -1 lµ sè chÝnh ph­¬ng.
Bài 6: (5 điểm) 
Cho f(x) = x3+bx2+cx+d
BiÕt f(1) = 3; f(2) = 8; f(3) = 15. TÝnh f(2009) vµ f(2010) (Tr×nh bµy lêi gi¶i vµ viÕt kÕt qu¶)
BiÕt f(x) Chia cho (x+3) d­ 1; chia cho (x-4) d­ 8, chia cho (x+3)(x-4) ®­îc th­¬ng lµ x-3 vµ cßn d­. H·y x¸c ®Þnh b,c,d (Tr×nh bµy lêi gi¶i vµ viÕt kÕt qu¶).
Bµi 7: (5 ®iÓm)
 Trªn m¨t ph¼ng to¹ ®é vu«ng gãc Oxy Cho c¸c ®iÓm A(1,8; 4,2) B(-2,1; -1,2); C(3,9; -4,1)
 Chu vi 	 
a) TÝnh chu vi tam gi¸c ABC
 SABC 	 
TÝnh diÖn tÝch tam gi¸c ABC
TÝnh c¸c gãc cña tam gi¸c ABC.
Bài 8: (5 điểm) 
Cho tam giác ABC có ; AB = 4cm ; AC = 6cm và trung tuyến AM. Từ B, kẻ BH vuông góc với AC tại H và từ M, kẻ MK vuông góc với AC tại K (H, K Î AC). Tính độ dài đường trung tuyến AM.
Bài 9: (5 điểm)
Cho tam giác ABC có AB = 8,91cm ; AC = 10,32cm và . Tính:
Độ dài đường cao BH.
Diện tích tam giác ABC.
Độ dài cạnh BC. 
Bài 10 (5 điểm): 
Cho ®­êng trßn t©m O néi tiÕp tam gi¸c ABC. Gäi E, M, F lµ c¸c tiÕp ®iÓm (MÎAB, E Î BC ; F Î AC ). §Æt AB = c; BC = a; CA = b.
LËp c«ng thøc tÝnh diÖn tÝch ΔEMF theo a, b, c.
b) ¸p dông tÝnh diÖn tÝch ΔEMF khi a = 5cm; b = 6cm; c = 7cm
SΔEMF = 
phßng Gd & ®t s¬n ®éng	 h­íng dÉn chÊm thi 
	chän häc sinh giái CÊp huyÖn
	 n¨m häc 2011 - 2012
 M«n : gi¶i to¸n b»ng m¸y tÝnh casio 
 Ngµy thi: 27 th¸ng 11 n¨m 2011
 Thêi gian: 150 phót (kh«ng kÓ thêi gian giao ®Ò)
Bài 1: (5 điểm)
Tính giá trị của các biểu thức sau và điền kết quả vào ô vuông:
 Mỗi câu đúng 1 điểm
A = 2 
B = 3 
 	a) A = 	 KQ: 
 b) B = 
D = 40,99744 
C = 
c) 
d) 
 e) Biếtt: cosA = 0,8516 ; tgB = 3,1725 ; sinC = 0,4351. 
E = 0,2066
Tính : E = cotg(A + B – C) ?
Bài 2: (5 điểm)
Tìm giá trị của x, y, z dưới dạng phân số (hoặc hỗn số) từ các phương trình sau rồi điền kết quả vào ô vuông : Mỗi câu đúng 2,5 điểm
x =
 a) 
y = 6
b) 
Bài 3: (5 điểm) Mỗi câu đúng 2,5 điểm
a = 1
b = 3
a) Tìm ccác số tự nhiên a và b biết rằng: 
 b)T×m sè tù nhiªn lín nhÊt, nhá nhÊt (t­¬ng øng ®Æt lµ a, b) cã d¹ng chia hÕt cho 7
C¸ch gi¶i
KÕt qu¶
Gi¶ sö sè lín nhÊt cã d¹ng lµ , khi ®ã ta ph©n tÝch = 192900+=7.27557+1+
+Tõ ®ã suy ra z=4 
a=192934
T­¬ng tù phÇn trªn
b=112133
Bµi 4:(5®iÓm) Mỗi câu đúng 2,5 điểm 
a) Tæng qu¸t ng­êi ®ã göi a ®ång l·i suÊt lµ r% 
Sau 1 th¸ng, tæng sè tiÒn (c¶ gèc vµ l·i) lµ: a(1+r%) ( ®ång)
Sau 2 th¸ng, tæng sè tiÒn (c¶ gèc vµ l·i) lµ: a(1+r%)2 ( ®ång)
Sau 3 th¸ng, tæng sè tiÒn (c¶ gèc vµ l·i) lµ: a(1+r%)3 (®ång)
Sau 1 n¨m, tæng sè tiÒn (c¶ gèc vµ l·i) lµ: a(1+r%)12 ( ®ång)
¸p dông víi a = 1000000 ; r = 0,4. BÊm trªn m¸y ®­îc kÕt qu¶ lÇn l­ît lµ : 
Sau 1 th¸ng
Sau 2 th¸ng
Sau 3 th¸ng
Sau 1 n¨m
Tæng sè tiÒn
1004000
1008016
1012048,064
1049070,208
b) NÕu cø mçi th¸ng ng­êi ®ã göi vµo ng©n hµng 1 triÖu ®ång vµ l·i xuÊt vÉn lµ 0,4% (c¸c th¸ng còng kh«ng rót l·i suÊt ra) th× sau mét n¨m ng­êi ®ã cã ®­îc sè tiÒn lµ:
Sè tiÒn sau 1 n¨m lµ: 12316622,09 ®ång. 
Bài 5: (5 điểm )
Cho U0 = 2; U1 = 3; Un + 1 = 3Un - 2Un - 1 ( n Î N* ) 
ViÕt quy tr×nh bÊm phÝm liªn tôc tÝnh Un ( n ≥ 3 ).
	(2 điểm)KÕt qu¶:
n
2
3
4
5
6
7
8
9
10
Un
5
9
17
33
65
129
257
513
1025
 (1 điểm)
b) TÝnh c¸c Un vµ dù ®o¸n sè h¹ng tæng qu¸t lµ Un = 2n + 1 ( n Î N )
Chøng minh b»ng quy n¹p:
Un + 1 = 3Un - 2Un - 1 = 3( 2n + 1) - 2( 2n - 1 + 1) = 3.2n + 3 - 2n - 2 = 2n + 1 + 1(®pcm).
* Do ®ã ta cã:
 U2n + Un + 1 - 1 = (22n + 1) + (2n + 1 + 1) - 1 = (2n)2 + 2.2n + 1 = (2n + 1)2 ( lµ sè chÝnh ph­¬ng ).	(2 điểm)
Bài 6: (5 điểm) Mỗi câu đúng 2,5 điểm
a) §Æt f’(x) = f(x) – (x-2) f(x) = f’(x) + x-2
L¹i cã f’(1) = f’(2) = f’(3) = 0 f’(x) chia hÕt cho (x-1)(x-2)(x-3) 
mµ f’(x) cã bËc lµ 3, hÖ sè bËc cao nhÊt lµ 1 nªn f’(x) = (x-1)(x-2)(x-3) f(x) = (x-1)(x-2)(x-3)+x-2
f(2009) = 8084294343 ; f(2010)= 8096384512 	
Thay x=2009; x=2010 TÝnh ®­îc: 
b) f(x) = (x+3)(x-4)(x-3) + mx+n (D­ lµ mx+n) ta cã:
f(-3) = m.(-3)+ n = 1
f(4) = m.4 + n = 8
gi¶i hÖ phương trình t×m ®­îc m =1; n=4. Tõ ®ã suy ra :
b = -4 ; c =-9; d=40.
Bµi 7: (5 ®iÓm)
Trªn m¨t ph¼ng to¹ ®é vu«ng gãc Oxy Cho c¸c ®iÓm A(1,8; 4,2) B(-2,1; -1,2); C(3,9; -4,1)
 Chu vi 21,88671	 
a) TÝnh chu vi tam gi¸c ABC
 SABC 21,855	 
TÝnh diÖn tÝch tam gi¸c ABC
TÝnh c¸c gãc cña tam gi¸c ABC.
(2 ®iÓm)
Bài 8: (5 điểm)
 Cho tam giác ABC có ; AB = 4cm ; AC = 6cm và trung tuyến AM. Từ B, kẻ BH vuông góc với AC tại H và từ M, kẻ MK vuông góc với AC tại K (H, K Î AC). Tính độ dài đường trung tuyến AM.
Cách giải: 
.Ta có 
 Nên AH = AB. cos cm
Mặt khác: BH//MK (gt) mà MB = MC
Suy ra KH = KC cm 
 và MK = ( vì MK là đường trung bình của ) (3 điểm)
 = 
Do đó = 2,64575 cm (2 điểm)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A
H
B
M
K
C
4
6
1200
Bài 9: (5điểm)
Cho tam giác ABC có AB = 8,91cm ; AC = 10,32cm và . Tính:
Độ dài đường cao BH.
Diện tích tam giác ABC.
Độ dài cạnh BC
 Cách giải:
Ta có BH = AB Sin = 8,91.sin720 
= 8,47391 cm 	 (2 ñieåm)đ
SABC = AC.BH = 10,32.8.474 
= 43,72539 cm2	(1 ñieåm)đ
Ta có AH = AB. cos = 8,91.cos720 
 Suy ra HC = AC – AH = 10,32 - 8,91.cos720
 Do đó BC = 
(2 ñieåm)đ
BH = 8,47391 cm
SABC = 43,72539 cm2
BC = 11,36053 cm 
Bài 10: Cho ®­êng trßn t©m O néi tiÕp tam gi¸c ABC. Gäi E, M, F lµ c¸c tiÕp ®iÓm (MÎAB, E Î BC ; F Î AC ). §Æt AB = c; BC = a; CA = b.
LËp c«ng thøc tÝnh diÖn tÝch ΔEMF theo a, b, c.
Cách giải:
TÝnh ®­îc 
(1®iÓm)
§Æt S1 = SΔAMF ; S2 = SΔBMF ; S3 = SΔCEF ; Ta cã:
 (1 ®iÓm)
	 (1 ®iÓm)
b) ¸p dông tÝnh diÖn tÝch ΔEMF khi a = 5cm; b = 6cm; c = 7cm
SΔEMF = 3. 359 3 cm2
 (2 ®iÓm)