Đề thi CASIO huyện Quế Sơn

UBND HUYỆN QUẾ SƠN
PHÒNG GD&ĐT
KỲ THI HỌC SINH GIỎI THỰC HÀNH
Môn: Giải toán trên máy CASIO lớp 9
Thời gian: 120 phút (Không kể thời gian giao đề)
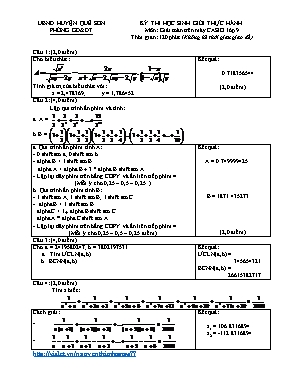
Câu 1: (2,0 điểm)
Cho biểu thức:
Tính giá trị của biểu thức với:
 x = 2,478369; y = 1,786452
Kết quả:
 0.718356544
(2,0 điểm)
Câu 2: (4,0 điểm)
Lập qui trình ấn phím và tính:
a. A = .
b.B = 
a. Qui trình ấn phím tính A: 
- 0 shift sto a; 0 shift sto b
- alpha B + 1 shift sto B
 alpha A + alpha B ¸ 3 ^ alpha B shift sto A
- Lặp lại dãy phím trên bằng COPY và ấn liên tiếp phím = 
(Mỗi ý cho 0,25 – 0,5 – 0,25 )
b. Qui trình ấn phím tính B: 
- 1 shift sto A; 1 shift sto B; 1 shift sto C
- alpha B + 1 shift sto B
 alpha C + 1¸ alpha B shift sto C
 alpha A * alpha C shift sto A
- Lặp lại dãy phím trên bằng COPY và ấn liên tiếp phím = 
(Mỗi ý cho 0,25 – 0,5 – 0,25 điểm)
Kết quả:
 A = 0.749999425
 B = 1871.435273
(2,0 điểm)
Câu 3: (4,0 điểm)
Cho a = 2419580247; b = 3802197531.
Tìm ƯCLN(a,b) 
 b. BCNN(a,b).
Kết quả:
ƯCLN(a,b) = 
 345654321
BCNN(a,b) = 
 26615382717
Câu 4: (2,0 điểm)
 Tìm x biết: 
Cách giải:
- 
- 
- 
(Mỗi ý cho 0,50 điểm)
Kết quả:
 x1 = 106.8316894
 x2 = -112.8316894
(0,5 điểm)
Câu 5: (2,0 điểm)
	Giải phương trình:
(Đoán nghiệm hoặc giải bằng phương pháp lặp để tìm một nghiệm. Chia đa thức để hạ xuống bậc 3. Sử dụng chức năng giải phương trình bậc ba của máy để giải.)
Kết quả:
x1 = 2
x2 = -5
x3 = 3
x4 = 4
(2,0 điểm)
Câu 6: (3,0 điểm)
	Dãy số {un} xác định như sau: u1 = 1, u2 = 2
với n lẻ
với n chẵn
a. Lập qui trình tính un.
b. Tính u5; u10; u15; u20.
a. Lập qui trình tính un:
- 1 shift sto A; 2 shift sto B
- Alpha B x 2,008 + Alpha A x 2,009 shift sto A 
 Alpha A x 2,008 - Alpha B x 2,009 shift sto B
- Lặp lại dãy phím trên bằng COPY và ấn liên tiếp phím = 
(0,25 – 0,50 – 0,25)
Kết quả:
 u5 = 4065204553
 u10 =3272558202
 u15 =1099255229
 u20 =8892514964
(Mỗi ý cho 0,5 điểm)
Câu 7: (3,0 điểm)
Dãy số {xn } xác định như sau: x0 = 3, 
a. Lập qui trình ấn phím để tính xn và tính x3 ; x6 ; x9 ; x12.
b. Tính x2009.
a. Qui trình ấn phím:
- 3 =
- ( √ 3 x - 1)/( + √ 3)
- Lặp lại phím = để có xn.
(Mỗi ý 0,25 điểm)
b. Cách tính:
- Để ý kết quả thấy kết quả lặp lại với chu kỳ N = 6
- 2009 chia 6 dư 5 nên x2009 = x5.
(Mỗi ý cho 0,5 điểm)
Kết quả:
x3  = 0.204634926
x6  = -4.886751346
x9  = 0.204634926
x12 = -4.886751346
x2009 = x5 = -1.127711849
(1,25 điểm)
Câu 8: (3,0 điểm)
Tam giác vuông ABC (Â=900) có AB = 3cm; AC = 4cm. AH, AD lần lược là đường cao, phân giác của tam giác. Tính chu vi của tam giác AHD.
Cách tính:
- Áp dụng pitago tính được BC = 5 (cm)
- BH = ; AH = 
- 
- AD = 
 CV = +
 +
(Mỗi ý cho 0,5 điểm)
Hình vẽ:
A
B
C
D
H
Kết quả:
 CV = 5.16722325
(1,0 điểm)
Câu 9: (3,0 điểm) Cho ba đường tròn bán kính bằng nhau và bằng 5cm, đôi một tiếp xúc nhau (hình vẽ). Tính diện tích hình giới hạn bởi ba đường tròn đó (phần được tô màu).
Cách tính:
- Tam giác O1O2O3 là tam giác đều có cạnh 10cm.
- Diện tích cần tính bằng diện tích O1O2O3 trừ diện tích ba quạt.
- Diện tích mỗi quạt bằng diện tích hình tròn do góc ở tâm bằng 600.
- S = 
(Mỗi ý cho 0,5 điểm)
Hình vẽ:
Kết quả:
 S = 4,031362019
(1,0 điểm)
Câu 10: (4,0 điểm) Hai đường tròn (O1) và (O2) có bán kính lần lược là r1 = 3cm và r2 = 1cm tiếp xúc ngoài với nhau tại I. CD là tiếp tuyến chung của hai đường tròn (CÎ (O1), DÎ (O2), C≠D). a. Tính số đo góc O2O1C.
b. Tính diện tích hình giới hạn bởi hai cung nhỏ và CD (Phần tô mầu)
Cách tính:
- Hạ O2H vuông góc với O1C. Có: 
 O1O2 = 3+ 1 = 4(cm).
 O1H = 3 -1 = 2(cm)
- O2O1H là nửa tam giác đều nên O2O1C = 600.
- S = SThang - Squạt 1 - Squạt 2 
- O2H = 
- Squạt 1 = S(O1)/6 ; Squạt 2 = S(O2)/3 
- S = 
(Mỗi ý cho 0,5 điểm)
Hình vẽ:O1
O2
C
D
I
Kết quả:
 O2O1C = 600
 S = 1.168616699
(1,0 điểm)
(Chỉ yêu cầu ghi kết quả S vì kết quả O2O1C đã thể hiện ở phần cách tính)