Đề ôn thi môn Toán học 12

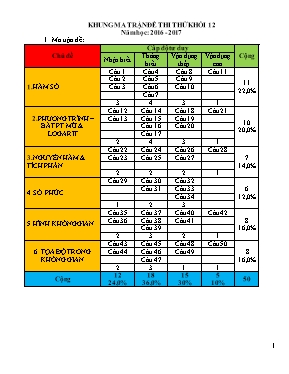
KHUNG MA TRẬN ĐỀ THI THỬ KHỐI 12
Năm học: 2016 - 2017
Ma trận đề: 
Chủ đề
Cấp độ tư duy
Cộng
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
1. HÀM SỐ 
Câu 1
Câu 4
Câu 8
Câu 11
11
22,0%
Câu 2
Câu 5
Câu 9
Câu 3
Câu 6
Câu 10
Câu 7
3
4
3
1
2. PHƯƠNG TRÌNH –BẤT PT MŨ & LOGARIT
Câu 12
Câu 14
Câu 18
Câu 21
10
20,0%
Câu 13
Câu 15
Câu 19
Câu 16
Câu 20
Câu 17
2
4
3
1
3. NGUYÊN HÀM & TÍCH PHÂN
Câu 22
Câu 24
Câu 26
Câu 28
7
14,0%
Câu 23
Câu 25
Câu 27
2
2
2
1
4. SỐ PHỨC
Câu 29
Câu 30
Câu 32
6
12,0%
Câu 31
Câu 33
Câu 34
1
2
3
5. HÌNH KHÔNG GIAN
Câu 35
Câu 37
Câu 40
Câu 42
8
16,0%
Câu 36
Câu 38
Câu 41
Câu 39
2
3
2
1
6. TỌA ĐỘ TRONG KHÔNG GIAN
Câu 43
Câu 45
Câu 48
Câu 50
 8
16,0%
Câu 44
Câu 46
Câu 49
Câu 47
2
3
1
1
Cộng
12
24,0%
18
36,0%
15
30%
5
10%
50
Mô tả đề kiểm tra
CHỦ ĐỀ
CÂU
MÔ TẢ
1. Hàm số 
Nhận biết:
Câu 1 : Tìm giá trị lớn nhất và nhỏ nhất. 
Câu 2 : Cho đồ thi hàm bậc 3 hay trùng phương, tìm điểm CĐ, CT.
Câu 3 : Tìm tiệm cận đứng hay ngang của hàm số nhất biến. 
Thông hiểu:
Câu 4: Tính giá trị cực trị của hàm bậc ba hoặc trùng phương. 
Câu 5 : Cho hàm bậc 3 hay trùng phương tìm khoảng tăng, giảm.
Câu 6 : Giao điểm của đường cong và đường thẳng. 
Câu 7 : Đồ thị hàm số. 
Vận dụng:thấp
Câu 8 : Tìm tham số để hàm số có cực trị. 
Câu 9 : Tiếp tuyến.
Câu 10 : Tính giá trị hàm số. 
Vận dụng cao
Câu 11 :Tìm m để hàm bậc 3 đồng hay nghịch biến trên (a;b
2. PHƯƠNG TRÌNH –BẤT PT MŨ & LOGARIT
Nhận biết:
Câu 12 : Công thức lôgarít. 
Câu 13 : Giải phương trình 
Thông hiểu:
Câu 14. Giải bất pt logarit cơ bản .
Câu 15 : Công thức lôgarit. 
Câu 16 : Đạo hàm hàm ln.
Câu 17 : Tính giá trị biểu thức.
Vận dụng thấp
Câu 18 : Biểu diễn lôgarit theo lôgarit. 
Câu 19 : Bất pt mũ giải bằng nhiều cách.
Câu 20 : Bài toán tham số. 
Vận dụng cao
Câu 21: Bài toán tham số.
3. NGUYÊN HÀM & TÍCH PHÂN
Nhận biết:
Câu 22 : Tính chất tích phân. 
Câu 23 : Kiểm tra công thức tính dthp hay thể tích vật tròn xoay .
Thông hiểu:
Câu 24 : Tìm nguyên hàm của f(x)
Câu 25 : Tìm một nguyên hàm F(x) của f(x) biết F(x0) = b.
Vận dụng:thấp
Câu 26 : Cho kết quả được biểu thị qua số m ,n tính m+n hay m.n.
Câu 27 : Tính kết hợp bởi 2 pp ( lưu ý hs không thể bấm máy được) .
Vận dụng cao
Câu 28 : Bài toán vận dụng tính diện tích hình phẳng.
4. SỐ PHỨC
Nhận biết:
Câu 29: Cho tọa độ M biểu diễn cho z tìm phần thực, ảo. 
Thông hiểu:
Câu 30 : Tìm mo-đun của z.
Câu 31 : Giải phương trình và nhân hai số phức. 
Vận dụng:thấp
Câu 32 : Tính mô đun số phức.
Câu 33 : Tìm số phức thỏa điều kiện. 
Câu 34 : Tìm số phức z thỏa điều kiện cho trước .
5. HÌNH KHÔNG GIAN 
Nhận biết:
Câu 35 : Tính chiều cao khối chóp.
Câu 36 : Thể tích khối lập phương. 
Thông hiểu:
Câu 37 : Tính thể tích khối chóp biết cạnh đáy và góc cạnh bên với đáy tính thể tích.
Câu 38 : Thể tích khối nón. 
Câu 39 : Tính thể tích khối trụ.
Vận dụng:thấp
Câu 40 : Tính thể tích khối chóp. 
Câu 41 : Tính thể tích khối chóp. 
Vận dụng cao
Câu 42 : Bài toán ứng dụng thực tế. 
6. TỌA ĐỘ TRONG KHÔNG GIAN 
Nhận biết:
Câu 43 : Tìm vecto chỉ phương. 
Câu 44 : Tìm trọng tâm.
Thông hiểu:
Câu 45 : Viết phương trình mặt phẳng trung trực của đoạn thẳng.
Câu 46 : Viết pt mặt cầu (S) biết tâm I và tiếp xúc mp ( P ) .
Câu 47 : Xét vị trí tương đối của hai đường thẳng.
Vận dụng:thấp
Câu 48 : Tìm tọa độ điểm thỏa mãn về thể tích tứ diện.
Câu 49 : Tìm bán kính mặt cầu tiếp xúc trong và tiếp xúc ngoài. 
Vận dụng cao
Câu 50 : Tính thể tích tứ diện.
ĐỀ ÔN THI 2017
Câu 1. Cho hàm số xác định, liên tục trên đoạn [-4;5] và có bảng biến thiên như sau:
 x
 -4 0 1 5
 y’
 + 0 - 0 +
 y
 9 
 -7 -3
Khẳng định nào sau đây là khẳng định đúng?
A.Giá trị nhỏ nhất của hàm số là -7, giá trị lớn nhất của hàm số là 6.
B. Giá trị nhỏ nhất của hàm số là -7, giá trị lớn nhất của hàm số là -3.
C. Giá trị nhỏ nhất của hàm số là 6, giá trị lớn nhất của hàm số là 9.
D. Giá trị nhỏ nhất của hàm số là -7, giá trị lớn nhất của hàm số là 9.
Câu 2. Cho hàm số xác định, liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ. Hàm số đạt cực tiểu tại điểm nào dưới đây? 
A. x=0.	B. 	C. 	D. x=2. 
Câu 3. Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số ?
A. x=3.	B. x=-3	C. x=2.	D. y=3. 
Câu 4. Tìm giá trị cực đại yCD của hàm số . 
A. 	B. 	C. 	D. 
Câu 5. Hàm số nghịch biến trên khoảng nào?
A. 	B. 	C. 	D. . 
Câu 6. Biết rằng đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt; kí hiệu là tọa độ của hai điểm đó. Tính 
A. 	B. 	C. 	D. 
Câu 7. Đồ thị hình bên là của hàm số nào?
 A. .
B. .
C. .
D. .
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số có ba điểm cực trị. 
A. 	B. 	C. 	D. 
Câu 9. Gọi có tung độ bằng 5. Tiếp tuyến của (C) tại M cắt các trục tọa độ Ox, Oy lần lượt tại A và B. Tính diện tích S của tam giác OAB?
A. 	B. 	C. 	D. 
Câu 10. Biết O(0;0), A(2;-4) là các điểm cực trị của đồ thị hàm số .
Tính giá trị của hàm số tại x=-2. 
A. 	B. 	C. 	D. 
Câu 11. Tìm tất cả các tham số thực m để hàm số luôn luôn nghịch biến trên 
A. 	B. 	C. 	D. 
Câu 12. Với các số thực dương a, b bất kì. Mệnh đề nào sau đây đúng? 
A. 	B. 
C. 	D. 
Câu 13. Tìm nghiệm của phương trình 
A. 	B. 	C. 	D. 
Câu 14. Tìm tập nghiệm S của bất phương trình 
A. 	B. 	C. 	D. 
Câu 15. Với các số thực dương a, b bất kì. Mệnh đề nào sau đây đúng? 
A. 	B. 
C. 	D. 
Câu 16. Đạo hàm của hàm số là.
	A. 	B. 	
C. 	D. .
Câu 17. Cho . Tính giá trị biểu thức 
A. 	B. 	C. 	D. 
Câu 18. Đặt . Hãy biểu diễn theo a và b. 
	A. 	B. 	
C. 	D. . 
Câu 19. Cho hàm số . Khẳng định nào sau đây là khẳng định sai?
A. 	B. 
C. 	D. 
Câu 20. Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình có hai nghiệm phân biệt sao cho 
A. m=4.	B. m=-4.	C. 	D. 
Câu 21. Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình có nghiệm. 
A. 	B. 	C. 	D. 
Câu 22. Biết rằng là một hàm số liên tục và có đạo hàm trên đoạn [0;2] và Tính . 
A. I=3	B. I=2	C. I=0	D. I=6. 
Câu 23. Viết công thức tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số liên tục, trục hoành và hai đường thẳng x=a, x=b với a<b. 
A. 	B. 	
C. 	D. 
Câu 24. Biết tích phân với a>0. Tìm a. 
A. a=1.	B. a=e.	C. a=2.	D. a=ln2. 
Câu 25. Biết F(x) là một nguyên hàm của hàm số và . Tính 
A. 	B. 	C. 	D. 
Câu 26. Biết tích phân với Tìm tổng a+b. 
A. 	B. 	C. 	D. . 
Câu 27. Một ôtô đang chạy với vận tốc 20m/s thì người lái đạp phanh. Sau khi đạp phanh, ôtô chuyển động chậm dần đều với vận tốc (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?
A. 10m.	B. 7m	.	C. 5m.	D. 3m.
Câu 28. Cho hình thang cong giới hạn bới các đường và . Đường thẳng chia thành hai phần có diện tích là và như hình vẽ bên. Tìm để .
A. 	 B. 	C. 	D. 
Câu 29. Cho số phức Tìm phần thực và phần ảo số phức 
A. Phần thực bằng 3 và phần ảo bằng 4.	B. Phần thực bằng 3 và phần ảo bằng -4.
C. Phần thực bằng 3 và phần ảo bằng 4i	D. Phần thực bằng 3 và phần ảo bằng -4i. 
Câu 30. Cho hai số phức . Tính mô đun số phức 
A. 	B. 	C. 	D. 
Câu 31. Kí hiệu là hai nghiệm phức của phương trình . Tính 
A. 	B. 	C. 	D. 
Câu 32. Kí hiệu là bốn nghiệm phức của phưong trình . Tính tổng 
A. 	B. 	C. 	D. 
Câu 33. Cho số phức z có phần ảo bằng 164 và với số nguyên dương n thỏa mãn Tìm n? 
A. n=697.	B. n=-656.	C. n=679. 	D. n=656. 
Câu 34. Tìm c biết a,b và c là các số nguyên dương thỏa mãn 
A. c=198.	B. c=189.	C. c=198 hoặc c=-198.	D. c=-198. 
Câu 35. Một hình chóp có điện tích đáy bằng 12m2 và thể tích khối chóp đó là 72m3. Chiều cao h của khối chóp là. 
A. 	B. 	C. 	D. . 
Câu 36. Tính thể tích V của khối lập phương ABCD.A’B’C’D’, biết .
A. 	B. 	C. 	D. 
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng a, góc , SA vuông góc với đáy, góc giữa SC và đáy bằng 600. Thể tích V của khối chóp S.ABCD là. 
A. 	B. 	C. 	D. . 
Câu 38. Cắt khối nón bởi một mặt phẳng qua trục tạo thành một tam giác ABC đều có cạnh bằng a; biết B, C thuộc đường tròn đáy. Thể tích của khối nón.
A. 	B. 	C. 	D. 
Câu 39. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Diện tích toàn phần của khối trụ là:
A. B. C. D.
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA vuông góc với đáy, biết khoảng cách từ điểm B đến mặt phẳng (SCD) bằng . Tính thể tích khối chóp S.ABCD. 
A. 	B. 	C. 	D. . 
Câu 41. Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh bằng a, SA vuông góc với đáy và SBD là một tam giác đều. Gọi M, N lần lượt là trung điểm SB và SD. Tính thể tích V của khối chóp A.OMN. 
	A. 	B. 	C. 	D. 
Câu 42. Từ tấm tôn hình chữ nhật cạnh 90cm x 180cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 80cm theo 2 cách (như hình minh họa bên dưới). 
Cách 1. Gò tấm tôn ban đầu thành mặt xung quanh của cái thùng.
Cách 2. Cắt tấm tôn ban đầu thành 3 tấm bằng nhau và gò các tấm đó thành mặt xung quanh của 3 cái thùng. 
Ký hiệu là thể tích của thùng gò được theo cách thứ nhất và là tổng thể tích của ba thùng gò được theo cách thứ 2. Tính tỉ số 
A. 	 B.	 C. 3	 D.2.
Câu 43. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: . Vecto nào dưới đây là một vecto chỉ phương của đường thẳng d? 
A. 	B. .	C. .	D. .
Câu 44. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;3), B(3;-2;-9), C(2;0;0). Tìm tọa độ trọng tâm G của tam giác ABC. 
A. G(2;0;-2).	B. G(6;0;-6).	C. G(3;0;-3).	D. G(2;0;2).
Câu 45. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;0;1), B(3;2;1). Phương trình nào dưới đây là phương trình của mặt phẳng trung trực của đoạn thẳng AB. 
A. 2x+y+z-6=0.	B. x+y-5=0.	C. x+y-3=0.	D. x+y-1=0.
Câu 46. Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới dây là phương trình của mặt cầu có tâm I(2;-1;3) và tiếp xúc với mặt phẳng (P): 4x+3y+45=0?
A. 	B. 
C. 	D. 
Câu 47. Cho hai đường thẳng d: và d’:. Mệnh đề nào dưới đây đúng?
A. d và d’ chéo nhau và vuông góc với nhau. 	B. d và d’ cắt nhau	
C. d và d’ chéo nhau	D. d và d’ vuông góc với nhau. 
Câu 48. Cho tứ diện ABCD với A(2;1;-1), B(3;0;1), C(2;-1;3), Tìm tọa độ điểm D để thể tích tứ diện bằng 5. 
A. 	B.	 
C. 	D. 	
Câu 49. Cho mặt cầu (S): Viết phương trình mặt cầu có tâm là gốc tọa độ và tiếp xúc với mặt cầu (S). 
A. 	B. 
C. 	D. 
Câu 50. Cho điểm S(0;0;1) và hai điểm M, N lần lượt chuyển động trên hai bán trục dương Ox, Oy sao cho OM+ON=1. Tính giá trị lớn nhất của thể tích tứ diện S.OMN. 
A. 	B. 	C. 	D. 
------Hết------
ĐÁP ÁN
1. Hàm số. 
Nhận biết. 
Câu 1. Cho hàm số xác định, liên tục trên đoạn [-4;5] và có bảng biến thiên như sau:
 x
 -4 0 1 5
 y’
 + 0 - 0 +
 y
 9 
 -7 -3
Khẳng định nào sau đây là khẳng định đúng?
A.Giá trị nhỏ nhất của hàm số là -7, giá trị lớn nhất của hàm số là 6.
B. Giá trị nhỏ nhất của hàm số là -7, giá trị lớn nhất của hàm số là -3.
C. Giá trị nhỏ nhất của hàm số là 6, giá trị lớn nhất của hàm số là 9.
D. Giá trị nhỏ nhất của hàm số là -7, giá trị lớn nhất của hàm số là 9.
Phương án nhiễu. Câu A lấy hai đầu mút, câu B lấy hai giá trị của y bên dưới, câu C lấy hai gái trị của y bên trên. 
Câu 2. Cho hàm số xác định, liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ. Hàm số đạt cực tiểu tại điểm nào dưới đây? 
A. x=0.	B. 	C. 	D. x=2. 
Phương án nhiễu. Câu B lấy x cực đại, câu C lấy -2 của đề hay hay trong hình, câu D lấy x=2 trong hình. 
Câu 3. Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số ?
A. x=3.	B. x=-3	C. x=2.	D. y=3. 
Phương án nhiễu. Câu B sai dấu trừ, câu C của tiệm cận ngang, câu D sai kí kiệu y. 
Thông hiểu.
Câu 4. Tìm giá trị cực đại yCD của hàm số . 
A. 	B. 	C. 	D. 
Phương án nhiễu. Câu B lấy y cực tiểu, câu C lấy x cực tiểu, câu D lấy x cực đại.
Câu 5. Hàm số nghịch biến trên khoảng nào?
A. 	B. 	C. 	D. . 
Phương án nhiễu. Câu B khoảng đồng biến, câu C lấy 2 giá trị cực trị, câu D vừa đồng biến vừa nghịch biến. 
Câu 6. Biết rằng đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt; kí hiệu là tọa độ của hai điểm đó. Tính 
A. 	B. 	C. 	D. 
Đáp án: 
Phương án nhiễu: Câu B lấy câu C câu D 
Câu 7. Đồ thị hình bên là của hàm số nào?
 A. .
B. .
C. .
D. .
Vận dụng thấp. 
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số có ba điểm cực trị. 
A. 	B. 	C. 	D. 
Phương án nhiễu. Câu B lấy m để hàm số có một cực trị, câu C lấy m để hàm số có một cực trị, câu D vừa có ba cực trị vừa có một cực trị.
Câu 9. Gọi có tung độ bằng 5. Tiếp tuyến của (C) tại M cắt các trục tọa độ Ox, Oy lần lượt tại A và B. Tính diện tích S tam giác OAB?
A. 	B. 	C. 	D. 
Đáp án: PTTT của (C) tại M(2;5): y = -3x+11; A(11/3;0); B(0;11). Diện tích tam giac OAB là 121/6. 
Câu 10. Biết O(0;0), A(2;-4) là các điểm cực trị của đồ thị hàm số .
Tính giá trị của hàm số tại x=-2. 
A. 	B. 	C. 	D. 
Câu B tính sai câu C tính sai câu D tính sai 
Ta có .
Yêu cầu bài toán 
Câu 10.
Vận dụng cao. 
Câu 11. Tìm tất cả các tham số thực m để hàm số luôn luôn nghịch biến trên 
A. 	B. 	C. 	D. 
Phương án nhiễu. Câu B thiếu dấu bằng, câu C và câu D chỉ đúng một trường hợp. 
Cách 1. 
Tập xác định: 
Tính 
Xét hàm số với . 
Yêu cầu đề 
Vì hàm là hàm bậc nhất nên: 
Cách 2. 
Tập xác định: 
Tính 
Đặt . 
Để hàm số luôn nghịch biến trên 
Trường hợp 1: 
Do 	
Để 
Vậy 
Trường hợp 2: 
Lúc đó 	
Để 
Vậy 
Đáp số: 
2. Phương trình mũ và lôgarit. 
Nhận biết.
Câu 12. Với các số thực dương a, b bất kì. Mệnh đề nào sau đây đúng? 
A. 	B. 
C. 	D. 
Câu 13. Tìm nghiệm của phương trình 
A. 	B. 	C. 	D. 
Phương án nhiễu: Câu B cho x-3 =1, câu C lấy , lấy 
Thông hiểu.
Câu 14. Tìm tập nghiệm S của bất phương trình 
A. 	B. 	C. 	D. 
Đáp án: 
Câu B học sinh chỉ giải 
Câu C học sinh chỉ giải 
Câu D học sinh giải bất phương trình sai 
Câu 15. Với các số thực dương a, b bất kì. Mệnh đề nào sau đây đúng? 
A. 	B. 
C. 	D. 
Câu 16. Đạo hàm của hàm số là.
	A. 	B. 	
C. 	D. .
Câu 17. Cho . Tính giá trị biểu thức 
A. 	B. 	C. 	D. 
Vận dụng thấp. 
Câu 18. Đặt . Hãy biểu diễn theo a và b. 
	A. 	B. 	
C. 	D. . 
Câu 19. Cho hàm số . Khẳng định nào sau đây là khẳng định sai?
A. 	B. 
C. 	D. 
Câu 20. Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình có hai nghiệm phân biệt sao cho 
A. m=4.	B. m=-4.	C. 	D. 
Phương án nhiễu: Câu B lấy gần giống đáp án, câu C lấy rồi suy ra m, câu D lấy rồi suy ra m. 
Đáp án. 
Đặt khi đó phương trình (1) có dạng: 
Để phương trình (1) có hai nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt tương ứng 
Vì 
Vậy để phương trình (1) có hai nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt sao cho 
Khi và chỉ khi 
Vận dụng cao. 
Câu 21. Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình có nghiệm. 
A. 	B. 	C. 	D. 
Phương án nhiễu: Là các tập con của phượng án đúng. 
Đáp án. 
Đặt 
Phương trình (1) trở thành 
Nếu không thỏa mãn. 
Nếu 
Biến đổi 
Xét hàm số lập bảng biến thiên ta được 
3. Tích phân.
Nhận biết.
Câu 22. Biết rằng là một hàm số liên tục và có đạo hàm trên đoạn [0;2] và Tính . 
A. I=3	B. I=2	C. I=0	D. I=6. 
Câu 23. Viết công thức tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số liên tục, trục hoành và hai đường thẳng x=a, x=b với a<b. 
A. 	B. 	
C. 	D. 
Thông hiểu.
Câu 24. Biết tích phân với a>0. Tìm a. 
A. a=1.	B. a=e.	C. a=2.	D. a=ln2. 
Câu 25. Biết F(x) là một nguyên hàm của hàm số và . Tính 
A. 	B. 	C. 	D. 
Phương án nhiễu. Câu B tính nguyên hàm có dấu trừ, câu C thế vào , câu D tính nguyên hàm thiếu chia 2. 
Vận dụng thấp.
Câu 26. Biết tích phân với Tìm tổng a+b. 
A. 	B. 	C. 	D. . 
Đáp án: 
Câu 27. Một ôtô đang chạy với vận tốc 20m/s thì người lái đạp phanh. Sau khi đạp phanh, ôtô chuyển động chậm dần đều với vận tốc (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?
A. 10m.	B. 7m	.	C. 5m.	D. 3m.
Đáp án: 
Vận dụng cao. 
Câu 28. Cho hình thang cong giới hạn bới các đường và . Đường thẳng chia thành hai phần có diện tích là và như hình vẽ bên. Tìm để .
A. 	 B. 	C. 	D. 
Đáp án: 
4. Số phức. 
Nhận biết.
Câu 29. Cho số phức Tìm phần thực và phần ảo số phức 
A. Phần thực bằng 3 và phần ảo bằng 4.	B. Phần thực bằng 3 và phần ảo bằng -4.
C. Phần thực bằng 3 và phần ảo bằng 4i	D. Phần thực bằng 3 và phần ảo bằng -4i. 
Câu B lấy thực và ảo của z, câu C sai 4i, câu D sai i nhưng của z.
Thông hiểu.
Câu 30. Cho hai số phức . Tính mô đun số phức 
A. 	B. 	C. 	D. 
Đáp án: 
Câu B ngược của đáp án, câu C thiếu căn, câu D tính sai 
Câu 31. Kí hiệu là hai nghiệm phức của phương trình . Tính 
A. 	B. 	C. 	D. 
Đáp án: 
Câu B tính Nên 
Câu C lấy hai số phức cộng lại. 
Câu D tính modun cộng lại. 
Vận dụng thấp.
Câu 32. Kí hiệu là bốn nghiệm phức của phưong trình . Tính tổng 
A. 	B. 	C. 	D. 
Đáp án: 
Câu B chỉ tính tổng mô đun 2 số phức. Câu C lấy thiếu lấy căn, câu D lấy 
Câu 33. Cho số phức z có phần ảo bằng 164 và với số nguyên dương n thỏa mãn Tìm n? 
A. n=697.	B. n=-656.	C. n=679. 	D. n=656. 
Phương án nhiễu. Câu B lấy phần thực của z, câu C gần giống đáp án, câu D lấy –a. 
Đáp án: 
Từ 
Câu 34. Tìm c biết a,b và c là các số nguyên dương thỏa mãn 
A. c=198.	B. c=189.	C. c=198 hoặc c=-198.	D. c=-198. 
Phương án nhiễu. Câu B đảo đáp án, câu C lấy a bằng 6 và a=-6, câu D lấy a=-6. 
Đáp án: 
Để c là số nguyên dương khi và chỉ khi 
Do a và b là số nguyên và số 107 là số nguên tố nênẫt có hai trường hợp.
5. Thể tích. 
Nhận biết.
Câu 35. Một hình chóp có điện tích đáy bằng 12m2 và thể tích khối chóp đó là 72m3. Chiều cao h của khối chóp là. 
A. 	B. 	C. 	D. . 
Câu 36. Tính thể tích V của khối lập phương ABCD.A’B’C’D’, biết .
A. 	B. 	C. 	D. 
Thông hiểu.
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng a, góc , SA vuông góc với đáy, góc giữa SC và đáy bằng 600. Thể tích V của khối chóp S.ABCD là. 
A. 	B. 	C. 	D. . 
Câu B thiếu chia 3, câu C tính sai diện tích hình thoi thiếu nhân 2, câu D tính diện tích hình thoi như hình vuông. 
Đáp án. 
Câu 38. Cắt khối nón bởi một mặt phẳng qua trục tạo thành một tam giác ABC đều có cạnh bằng a; biết B, C thuộc đường tròn đáy. Thể tích của khối nón.
A. 	B. 	C. 	D. 
Bán kính đáy khối nón là , chiều cao khối nón là , suy ra , chọn C.
Câu 39. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Diện tích toàn phần của khối trụ là:
A. B. C. D.
Đáp án: Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng 3a
Ta có : l=h=2r=3a.
Diện tích toàn phần của khối trụ là: S=
Vận dụng thấp.
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA vuông góc với đáy, biết khoảng cách từ điểm B đến mặt phẳng (SCD) bằng . Tính thể tích khối chóp S.ABCD. 
A. 	B. 	C. 	D. . 
Đáp án. 
. 
Câu 41. Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh bằng a, SA vuông góc với đáy và SBD là một tam giác đều. Gọi M, N lần lượt là trung điểm SB và SD. Tính thể tích V của khối chóp A.OMN. 
	A. 	B. 	C. 	D. 
Ta có: 
Tính thể tích khối chóp 
Ta có: 
Nên 
Tính 
Hoặc 
. 
Vậy 
Vận dụng cao. 
Câu 42. Từ tấm tôn hình chữ nhật cạnh 90cm x 180cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 80cm theo 2 cách (như hình minh họa bên dưới). 
Cách 1. Gò tấm tôn ban đầu thành mặt xung quanh của cái thùng.
Cách 2. Cắt tấm tôn ban đầu thành 3 tấm bằng nhau và gò các tấm đó thành mặt xung quanh của 3 cái thùng. 
Ký hiệu là thể tích của thùng gò được theo cách thứ nhất và là tổng thể tích của ba thùng gò được theo cách thứ 2. Tính tỉ số 
A. 	 B.	 C. 3	 D.2.
Đáp án. 
Vì các thùng đều có chung chiều cao nên: 
+) Diện tích đáy 1:
	Chu vi đáy 1: =180 =. 	=
+) Diện tích đáy 2: 
	Chu vi đáy 2: =60 =. 	=3=
Vậy =3.
6. Hình học không gian. 
Nhận biết.
Câu 43. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: . Vecto nào dưới đây là một vecto chỉ phươn