Đề ôn tập kiểm tra trắc nghiệm Chương 1 môn Giải tích Lớp 12 (Cơ bản)

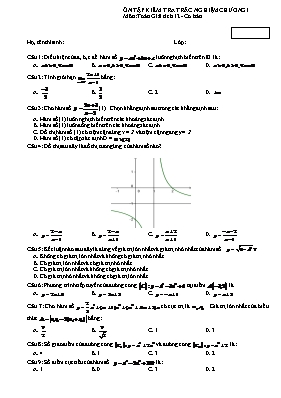
ÔN TẬP KIỂM TRA TRẮC NGHIỆM CHƯƠNG 1
Môn: Toán Giải tích 12 - Cơ bản
Họ, tên thí sinh:............................................................................. Lớp: .............................
Câu 1: Điều kiện của a, b, c để hàm số luôn nghịch biến trên là:
A. 	B. 	C. 	D. 
Câu 2: Tính giới hạn bằng:
A. 	B. 	C. 2	D. 
Câu 3: Cho hàm số (1) . Chọn khẳng định sai trong các khẳng định sau:
A. Hàm số (1) luôn nghịch biến trên các khoảng xác định
B. Hàm số (1) luôn đồng biến trên các khoảng xác định
C. Đồ thị hàm số (1) có tiệm cận đứng x = 2 và tiệm cận ngang y = 2
D. Hàm số (1) có tập xác định D = 
Câu 4: Đồ thị sau đây là đồ thị tương ứng của hàm số nào?
A. 	B. 	C. 	D. 
Câu 5: Kết luận nào sau đây là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
A. Không có giá trị lớn nhất và không có giá trị nhỏ nhất
B. Có giá trị lớn nhất và có giá trị nhỏ nhất
C. Có giá trị lớn nhất và không có giá trị nhỏ nhất
D. Có giá trị nhỏ nhất và không có giá trị lớn nhất
Câu 6: Phương trình tiếp tuyến của đường cong tại điểm là
A. 	B. 	C. 	D. 
Câu 7: Cho hàm số có cực trị là . Giá trị lớn nhất của biểu thức bằng:
A. 	B. 	C. 1	D. 3
Câu 8: Số giao điểm của đường cong và đường cong là:
A. 4	B. 1	C. 3	D. 2
Câu 9: Số điểm cực tiểu của hàm số là:
A. 1	B. 0	C. 3	D. 2
Câu 10: Đồ thị sau đây là đồ thị tương ứng của hàm số nào?
A. 	B. 
C. 	D. 
Câu 11: Tập xác định của hàm số là:
A. 	B. 	C. 	D. 
Câu 12: Cho hàm số . Kết luận nào sau đây đúng?
A. Hàm số có cực đại và cực tiểu nằm về cùng 1 phía của trục tung
B. Hàm số có cực đại và cực tiểu nằm về hai phía của trục tung
C. Hàm số không có cực trị
D. Cả ba phương án A, B, C đều sai
Câu 13: Giá trị m để hàm số không có cực trị là:
A. 	B. 	C. 	D. 
Câu 14: Phương trình tiếp tuyến của đường cong đi qua điểm là:
A. 	B. 	C. 	D. 
Câu 15: Chọn phát biểu đúng trong các phát biểu sau.Trên khoảng thì hàm số :
A. Có giá trị lớn nhất là Maxy = 1	B. Có giá trị lớn nhất là Maxy = 2
C. Có giá trị nhỏ nhất Miny =1	D. Có giá trị nhỏ nhất Miny = 2
Câu 16: Tọa độ giao điểm có hoành độ nhỏ hơn 1 của đường và đường thẳng là:
A. 	B. 	C. 	D. 
Câu 17: Hàm số nghịch biến trên:
A. 	B. 	C. 	D. 
Câu 18: Đồ thị sau đây là đồ thị tương ứng của hàm số nào?
A. 	B. 	C. 	D. 
Câu 19: Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [0;3] là:
A. M = 3 ; m = -1	B. M = 0; m = 2	C. M = 6; m = 1	D. M = 3; m = 1
Câu 20: Tất cả các giá trị của m để đường cắt đường tại bốn điểm phân biệt là:
A. 	B. 	C. 	D. 
Câu 21: Gọi lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số Khi đó, bằng:
A. 	B. 	C. 	D. 9
Câu 22: Trên đoạn [0;2] hàm số đạt giá trị lớn nhất tại x bằng giá trị nào sau đây:
A. x = 0	B. x = 2	C. x = 3	D. x = -
Câu 23: Phương trình tiếp tuyến của đường cong tại giao điểm có hoành độ âm của với đường thẳng là
A. 	B. 	C. 	D. 
Câu 24: Cho hàm số có đồ thị (C). Đường thẳng cắt đồ thị (C) tại 2 điểm phân biệt M và N thì tung độ trung điểm I của đoạn thẳng MN bằng:
A. 1	B. -2	C. 	D. -3
Câu 25: Đồ thị hàm số có các đường tiệm cận là:
A. Tiệm cận đứng x = 1; tiệm cận ngang y = -1
B. Tiệm cận đứng x = -1; tiệm cận ngang y = -1
C. Tiệm cận đứng y = 1; tiệm cận ngang x = -1
D. Tiệm cận đứng x = -1; tiệm cận ngang y = 1
Câu 26: Phương trình có 4 nghiệm phân biệt khi:
Câu 27: Cho hàm số. Hàm số có giá trị cực đại, giá trị cực tiểu trên đoạn là?
A.
B. 
C. 
D. 
Câu 28: Cho hàm số. (m là tham số). Với giá trị nào của m thì hàm số đi qua điểm (1;2)?
A. 
B. 
C. 
D. 
Câu 29: Đồ thị sau đây là của hàm số nào ? Chọn 1 câu đúng.
A. B. C. D. 
Câu 30. Hàm số đồng biến trên tập xác định của nó khi: 
A. B. C. D. 
Câu 31: Giá trị của m để hàm số nghịch biến trên là:
	A. 	B. 	C. 	D. 
Câu 32: Hàm số đạt cực tiểu tại x = 2 khi :
A. Không tồn tại m 	B. m = -1 	 C.m=1	 D. 
Câu 33.Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số có 3 điểm cực trị tạo thành một tam giác vuông cân.
Câu 34.Trong tất cả các hình chữ nhật có diện tích S, chu vi của hình chữ nhật có chu vi nhỏ nhất bằng bao nhiêu:
A. 	B. 	C. 	D. 
Câu 35. Cho hàm số . Phương trình: có hai nghiệm phân biệt khi m bằng. 
A. B. C. D.