Đề minh họa môn Toán - Đề 2

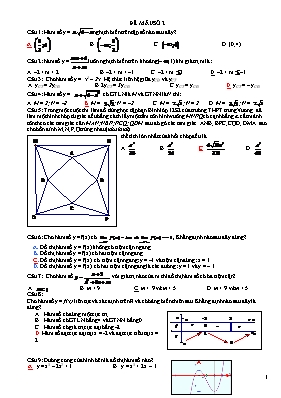
ĐỀ MẪU SỐ 2
Câu 1: Hàm số y = nghịch biến trên tập số nào sau đây? 
A. B. C D. (0;4)
Câu 2: hàm số y =luôn nghịch biến trên khoảng (–;1) khi giá trị m là:
A. –2 < m < 2 B. –2 < m < –1 C. –2 < m 1 D. –2 < m –1
Câu 3: Cho hàm số y = x3 – 2x . Hệ thức liên hệ giữa yCĐ và yCT.
 A. yCT = 2yCĐ B.2 yCT = 3yCĐ C. yCT = yCĐ D. yCT = – yCĐ 
Câu 4: Hàm số y = có GTLN là M và GTNN là N thì:
A. M = 2; N = –2 B. M = ; N = –2 C. M = ; N = 2 D. M = ; N = 
Câu 5: Trong một cuộc thi làm đồ dùng học tập bạn Bình lớp 12S2 của trường THPT trưng Vương đã làm một hình chóp tứ giác đều bằng cách lấy một tấm tôn hình vuông MNPQ có cạnh bằng a, cắt mảnh tôn theo các tam giác cân MAN; NBP; PCQ; QDM sau đó gò các tam giác ANB; BPC; CQD; DMA sao cho bốn đỉnh M;N;P;Q trùng nhau (như hình)
thể tích lớn nhất của khối chóp đều là
A. B. C. D. 
Câu 6: Cho hàm số y = f(x) có , Khẳng định nào sau đây đúng?
A. Đồ thị hàm số y = f(x) không có tiệm cận ngang
B. Đồ thị hàm số y = f(x) có hai tiệm cận ngang
C. Đồ thị hàm số y = f(x) có tiệm cận ngang: y = –1 và tiệm cận đứng: x = 1
D. Đồ thị hàm số y = f(x) có hai tiệm cận ngang là các đường: y = 1 và y = – 1
Câu 7: Cho hàm số với giá trị nào của m thì đồ thị hàm số có ba tiệm cận?
 A. B. m > 9 C. m 9 và m ¹ 5 
Câu 8: 
Cho hàm số y = f(x) liên tục và xác định trên R và có bảng biến thiên sau. Khẳng định nào sau đây là đúng?
Hàm số có đúng một cực trị. 
Hàm số có GTLN bằng 4 và GTNN bằng 0
Hàm số có giá trị cực đại bằng –2
D. Hàm số đạt cực đại tại x = -2 và đạt cực tiểu tại x = 2
Câu 9: Đường cong của hình bên là đồ thị hàm số nào? 
 A. y = x3 – 2x2 + 1 B. y = x3 + 2x – 1 
 C. y = x4 – 2x2 + 1 D. y = – x3 + 2x2 – 1 
Câu 10: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 
 có ba điểm cực trị tạo thành một tam giác đều.
A. m = B. m = 1 C. m = D. m Î Æ
Câu 11: (H) là đồ thị của hàm số y = và đường thẳng d: y = kx + 1. Để d cắt (H) tại hai điểm phân biệt A và B, sao cho M(–1;– 4) là trung điểm của đoạn thẳng AB. Thì giá trị thích hợp của k là:
A. 4 B. 6 C. 3 D. 5
Câu 12: Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kếp kỳ hạn một quý với lãi suất 1,65% một quý. Sau bao lâu người đó có được ít nhất 20 triệu đồng ( cả vốn lẫn lãi) từ vốn ban đầu ( với lã suất không thay đổi)
A. 52 tháng B. 54 tháng C. 36 tháng D. 60 tháng
Câu 13: Cho a > 0 vµ a ¹ 1. T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau: 
	A. cã nghÜa víi "x 	B. loga1 = a vµ logaa = 0
	C. logaxy = logax.logay	D. (x > 0,n ¹ 0)
Câu 14: Cho ; . Tính theo a, b bằng
A. 2a + b B. 2a + b – 1 C. 2a + b + 1 D. a + b – 2 .
Câu 15: Giả sử ta có hệ thức a2 + 4b2 = 12ab (a, b > 0). Hệ thức nào sau đây là đúng?
A. 	B. 
C. 	D. 
Câu 16: Cho f(x) = . §¹o hµm f’(0) b»ng:
	A. 2	B. ln2	 C. 2ln2	D. 1
Câu 17: Hµm sè y = cã tËp x¸c ®Þnh lµ:
	A. D = (0; +¥)	B.D = (-¥; 0)	C. D = (2; 3)	D. D = (-¥; 2) È (3; +¥)
Câu 18: Cho f(x) = x2e-x. bÊt ph­¬ng tr×nh f’(x) ≥ 0 cã tËp nghiÖm lµ:
	A. (2; +¥)	B. [0; 2]	C. (-2; 4]	D. [–2;3] 
Câu 19: Giải phương trình: ta được nghiệm :
	A. x = 24	B. x = 36	C. x = 45	 D. x = 64
Câu 20: Bất phương trình: có tập nghiệm là:
	A. (0; +∞)	B. 	 C. 	 D. 
Câu 21: §Ó gi¶i bÊt ph­¬ng tr×nh: ln > 0 (*), mét häc sinh lËp luËn qua ba b­íc nh­ sau:
	B­íc1: §iÒu kiÖn: Û (1)
	B­íc2: Ta cã ln > 0 Û ln > ln1 Û (2)
	B­íc3: (2) Û 2x > x - 1 Û x > -1 (3)
	KÕt hîp (3) vµ (1) ta ®­îc 
	VËy tËp nghiÖm cña bÊt ph­¬ng tr×nh lµ: (-1; 0) È (1; +¥)
	Hái lËp luËn trªn ®óng hay sai? NÕu sai th× sai tõ b­íc nµo?
	A. LËp luËn hoµn toµn ®óng	B. Sai tõ b­íc 1	C. Sai tõ b­íc 2	D. Sai tõ b­íc 3
Câu 22 : Tính tích phân .
A.	.	B. .	C.	.	D.	.
Câu 23 : Cho đường cong . Với mỗi , gọi là diện tích của phần hình thang cong đã cho nằm giữa hai đường vuông góc với trục Ox tại điểm có hoành độ 0 và . Khi đó 
A.	.	B.	.	C.	.	D.	.
Câu 24 : Tìm nguyên hàm của hàm số .
A.	.	B.	.
C.	D.	
Câu 25 : Tính tích phân .
A.	.	B.	.	C.	.	D.	.
Câu 26 : Ký hiệu K là khoảng hoặc đoạn hoặc nửa khoảng của . Cho hàm số xác định trên K. Ta nói được gọi là nguyên hàm của hàm số trên K nếu như :
A.	, C là hằng số tuỳ ý.	B.	.
C.	, C là hằng số tuỳ ý.	D.	
Câu 27 : Tập hợp các điểm biểu diễn số phức trên mặt phẳng toạ độ thoả mãn điều kiện là : 
A.	Đường thẳng đi qua hai điểm và .	B.	Hai điểm và . 
C.	Đường tròn tâm , bán kính .	D.	Đường tròn tâm , bán kính .
Câu 28 : Cho số phức . Môđun của số phức là 
A.	.	B.	3	C.	5	D.	4
Câu 29 : Cho xác định trên khoảng . Biến đổi nào sau đây là sai ?
A.	B.	
C.	D.	, C là một hằng số.
Câu 30 : Gọi là ba nghiệm của phương trình . Tính .
A.	B.	.	C.	.	D.	.
Câu 31 : Giải phương trình sau trên tập số phức : 
A.	.	B.	.	C.	.	D.	.
Câu 32 : Cho chuyển động thẳng xác định bởi phương trình , được tính bằng giây, được tính bằng mét. Tìm vận tốc của chuyển động tại (giây).
A.	.	B.	C.	.	D.	
Câu 33 : Tính diện tích hình phẳng giới hạn bởi hai đường và .
A.	.	B.	.	C.	.	D.	.
Câu 34 : Tìm số phức , biết .
A.	.	B.	.	C.	.	D.	.
Câu 35. Đường chéo của một hình hộp chữ nhật bằng d, góc giữa đường chéo và mặt đáy là , góc nhọn giữa hai đường chéo của đáy bằng . Thể tích của hình hộp đó là:
A. 	 	B. 	 
C. 	D. 
Câu 36. Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh 2a, SA = a, và mặt bên (SAB) vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AB, BC. Khi đó thể tích của khối chóp S.MBND là:
	A. 	B. 	C. 	D. Kết quả khác.
Câu 37. Cho tứ diện ABCD. Gọi B’ và C’ lần lượt thuộc các cạnh AB và AC thỏa và . Khi đó tỉ số thể tích của hai khối tứ diện bằng:
A. 	B. 	C. 	D. 
Câu 38. Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD = a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB, SC tạo với đáy một góc . Khoảng cách từ A đến mặt phẳng (SCD) là:
 	A. 	 	B. 	 	C. 	D. 
Câu 39. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón là:
A. 	B. 	C. 	D. 
Câu 40. Để làm cống thoát nước cho một khu vực dân cư người ta cần đúc 500 ống hình trụ có đường kính trong và chiều cao của mỗi ống bằng 1m, độ dày của thành ống là 10 cm. Chọn mác bê tông là 250 (tức mỗi khối bê tông là 7 bao xi măng). Hỏi phải chuẩn bị bao nhiêu bao xi-măng để làm đủ số ống nói trên.
	A. 	B. 	C. 	D. 
Câu 41. Một hình trụ có bán kính đáy bằng , thiết diện qua trục là một hình chữ nhật ABCD với AD = 2AB và AD song song với trục của hình trụ. Khi đó diện tích xung quanh hình trụ là:
	A. 	B. 	C. 	D. 
Câu 42. Bán kính mặt cầu ngoại tiếp hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên cùng bằng a là:
	A. 	B. 	C. 	D. 	
Câu 43. Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 4x – 6y – 10z + 5 = 0. Tìm khẳng định sai trong các khẳng định sau:
	A. Một vectơ pháp tuyến của (P) là B. Mặt phẳng này cắt cả ba trục tọa độ.
C. Điểm 	D. Mặt phẳng (P) có cặp VTCP là .
Câu 44. Trong không gian với hệ tọa độ Oxyz , phương trình mặt cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P) có phương trình là:
	A. 	B. 
	C. 	D. 
Câu 45. Trong không gian với hệ tọa độ Oxyz cho . Gọi M là điểm thuộc cạnh BC sao cho MC = 2MB. Độ dài của đoạn AM là:
	A. 	B. 	C. 	D. 
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: và mặt phẳng (P): . Giá trị nào của m để đường thẳng (d) vuông góc với mặt phẳng (P).
	A. 	B. 	C. 	D. 
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: và mặt phẳng (P):. Điểm M nào dưới đây thuộc đường thẳng (d) và cách mặt phẳng (P) một đoạn bằng 2?
	A. B. C. D. 
Câu 48. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x = 2t - 1; y = t; z = 3t – 5 nằm trên mặt phẳng (P) , thì tổng bằng giá trị nào dưới đây:
	A. 3	B. 2	C. 4	D. 0
Câu 49. Trong không gian với hệ tọa độ Oxyz cho các điểm và đường thẳng (d):. Tìm tọa độ của điểm M thuộc (d) để thể tích của tứ diện MABC bằng 3.
	A. 	B. 
	C. 	D. 
Câu 50. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, AB = a và . M là trung điểm của AA’ . Thể tích của khối tứ diện MA’BC’ theo a là:
	A. 	B. 	C. 	D. Kết quả khác.
	HƯỚNG DẨN GIẢI CHI TIẾT 
1A
2D
3D
4B
5C
6C
7C
8D
9A
10A
11D
12B
13D
14C
15A
16B
17C
18B
19D
20B
21D
22B
23C
24B
25B
26B
27C
28C
29B
30C
31C
32A
33C
34C
35A
36A
37D
38C
39A
40B
41A
42B
43D
44B
45C
46B
47B
48A
49A
50B
Câu 1. A. 
 Gợi ý: TXĐ: D = (–¥;4]
 + y’ = lập BBT suy ra hàm số nghịch biến 
Câu 2. D. –2 < m 
Gợi ý: TXĐ D = 
 + y’ = 
 Hàm số nghịch biến trên từng khoảng xác định Û m2 – 4 < 0 Û – 2 < m < 2
 Để hàm số nghịch biến trong khoảng (–¥; 1) Û (–¥; 1) Í (–¥; – m) Û 1 £ – m Û m £ – 1
 Kết hợp ĐK Þ –2 < m 
Câu 3. D. yCT = – yCĐ 
 Gợi ý: + y = x3 – 2x 
 + TXĐ : D = 
 + y’ = 3x2 – 2 = 0 
Câu 4. B. M = ; N = –2 
Gợi ý: y = 
 + TXĐ: D = [–2;2]
 + y’ = = 0 
 + y(2) = 2; y(–2) = – 2 
Câu 5. C. 
 Gợi ý: Gọi cạnh hình vuông ABCD là x thì đường cao mặt bên là: SM= suy ra chiều cao của phối chóp SO = Vậy V = lập bbt suy ra V lớn nhất tại x = 
Ta tìm maxV = 
Câu 6. C. Đồ thị hàm số y = f(x) có tiệm cận ngang: y = –1 và tiệm cận đứng: x = 1
Câu 7. C. m < 9 và m ¹ 5 
Gợi ý: 
 + Để hàm số có ba tiệm cận Û x2 + 6x + m = 0 phải có hai nghiệm phân biệt khác –5 Û m < 9 và m ¹ 5 
Câu 8. D. Hàm số đạt cực đại tại x = -2 và đạt cực tiểu tại x = 2
Câu 9. A. y = x3 – 2x2 + 1 
Câu 10. A. m = 
Gợi ý: y = x4 + 2(m – 2)x2 + m2 – 5m + 5 
 + y’ = 4x3 + 4(m – 2)x 
 + Để hàm số có ba cực trị Û y’ = 0 có ba nghiệm phân biệt Û m < 2 
 + y’ = 0 
 + Ba điểm cực trị của đồ thị: A(0;m2 – 5m + 5); 
 + ABC là tam giác đều Û AB = BC Û ( 2 – m) + (2 – m)4 = 4(2 – m)
 Û (2 – m)[(2 – m)3 – 3] = 0 Þ m = 
Câu 11. D. 5
 + Phương trình hoành độ giao điểm của (H) và d: = kx + 1 Û kx2 + 2kx – 2 = 0 (1)
 + Để có hai gđ Û (1) có hai nghiệm x1 và x2 khác – 2 Û k2 + 4k > 0 Û k 0
 + Ta luôn có Vậy ta có d phải qua M Û k = 5
Câu 12. B. 54 tháng 
Gợi ý: Số tiền cả vốn lẫn lãi người gửi sẽ có sau n quý: 
 S = 15( 1 + 0,0165)n = 15.1,0165n ( triệu đồng) 
 Suy ra logS = log15 + nlog1,0165 hay n = 
 Để có được số tiền 20 triệu đồng thì phải sau một thời gian: n = (quý) 
 » 54 tháng
Câu 13. D. (x > 0,n ¹ 0)
Câu 14. C. 2a + b + 1
Gợi ý : 
Câu 15. A. 
Gợi ý: a2 + 4b2 = 12ab Û (a + 2b)2 = 16ab Û 
 Û 
Câu 16. B. ln2
Gợi ý: f(x) = . Þ f’(0) = ln2
Câu 17. C. D = (2; 3)
 Gợi ý: y = 
 HSXĐ Û – x2 + 5x – 6 > 0 Û 2 < x < 3
Câu 18. B. [0; 2]
Gợi ý: f(x) = x2e-x.
 + f’(x) ≥ 0 Û e–x(2x – x2) ³ 0 Û 0 £ x £ 2
Câu 19. D. x = 64
Gợi ý : 
Câu 20. B. 
Gợi ý: (1) Điều kiện: 
 (1) Þ 3x – 2 > 6 – 5 x Û x > 1 
Câu 21. D. Sai tõ b­íc 3
Câu 22. B. .
Dùng máy tính được , chọn B.
Câu 23. C.	.
Từ định nghĩa tích phân, . Chọn C.
Câu 24. B.	.
. Chọn B.
Câu 25. B.	.
Dùng máy tính được . Chọn B.
Câu 26. B.	.
Theo định nghĩa nguyên hàm chọn B.
Câu 27. C.	Đường tròn tâm , bán kính .
 (với M là điểm biểu diễn số phức z, I(0;1)) => M nằm trên đường tròn tâm , bán kính . Chọn C.
Câu 28. C.	
. Chọn C.
Câu 29. B.	
Vì nên không biến đổi được . Chọn B.
Câu 30. C.	.
, nên . Chọn C.
Câu 31. C.	.
Bấm máy tính nhập biểu thức VT – VP , dùng chức năng CALC lần lượt thay các giá trị của các phương án, chọn được . Chọn C.
Câu 32. A.	.
Ta có vận tốc của chuyển động , do đó . Chọn A.
Câu 33. C.	.
. Diện tích cần tìm là 
Câu 34. C.	.
Bấm máy tính nhập biểu thức VT – VP , dùng chức năng CALC lần lượt thay các giá trị của các phương án, chọn được . Chọn C.
Câu 35. A. 
HD giải: 
Tính được: và 
Tính được : 
Tính được: 
Câu 36. A. 
HD giải: Gọi là chiều cao khối chóp.Vì tam giác SAB vuông tại S 
Diện tích tứ giác BMDN là: 
Câu 37. D. 
HD giải: Áp dụng bài toán tỉ số thể tích. 
Câu 38. C. 
HD giải:
+ Khoảng cách từ A đến mặt phẳng (SCD) là độ dài đoạn HK
+ Tính được 
+ Dùng công thức: 
+ Suy được : 
Câu 39. A. 
HD giải: ( đơn giản áp dụng công thức)
Câu 40. B. 
HD giải:
+ Tính thể tích khối trụ bán kinh 0,6m: 
+ Tính thể tích khối trụ bán kinh 0,5m: 
+ Lượng hồ bê tông cho một ống là: 
+ Lượng hồ bê tông để làm 500 ống là: 
+ Số lương bao xi-măng cần mua là 1.209,1532(bao)
Câu 41. A. 
HD giải: ( đơn giản áp dụng công thức)
Câu 42. B. 
HD giải:
	+ R = 
Câu 43. D. Mặt phẳng (P) có cặp VTCP là 
HD giải:
Dễ thấy cặp vectơ cùng phương thì không làm được VTCP cho mặt phẳng.
Tự kiểm chứng ba phương án còn lại đều đúng.
Câu 44. B. 
HD giải: + Tính 	chọn B.
Câu 45. C. 
Câu 46. B. 
HD giải: Dùng điều kiện hai vectơ cùng phương. 
Câu 47. B. 
HD giải:
+ Thay tọa độ các điểm M vào phương trình của (d) loại A, D.
+ Thay tọa độ điểm M của hai phương án B, C vào công thức tính khoảng cách loại C.
Câu 48. A. 3
HD giải:
Theá phöông trình d vaøo phöông trình cuûa , ta ñöôïc :
	m(2t – 1) + t – n(3t – 5) – 4n = 0 Û (2m – 3n + 1)t – m + n = 0 (1)
	Ñeå d Ì thì (1) thoûa vôùi moïi t Û Û m = n = 1. 	Vaäy m + 2n =3
Câu 49. A. 
Câu 50. B. 
HD giải: + Dùng phương pháp tọa độ.