Đề kiểm tra một tiết Toán 12 chương I (Hình học) ban cơ bản

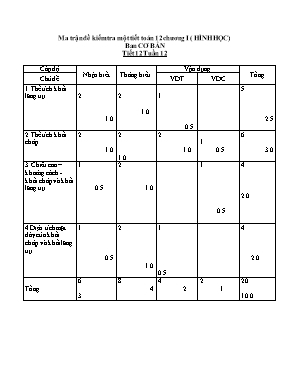
Ma trận đề kiểm tra một tiết toán 12 chương I ( HÌNH HỌC)
Ban CƠ BẢN
Tiết 12 Tuần 12
Cấp độ
Nhận biết
Thông hiểu
Vận dụng
Tổng
Chủ đề
VDT
VDC
1.Thể tích khối lăng trụ.
2
1.0
2	
 1.0
1
	0.5
5
2.5
2.Thể tích khối chóp.
2
1.0
2
	1.0
2
 1.0
1	
 0.5 
6
3.0
3.Chiều cao –khoảng cách -khối chóp và khối lăng trụ.
1
 0.5
2
1.0
1
	0.5
4
 2.0
4.Diện tích mặt đáy của khối chóp và khối lăng trụ
1
0.5
2
1.0
1
	0.5
4	
 2.0
Tổng
6
 3 
8
 4
4
 2 
2
 1
20
 10.0 
Đề kiểm tra 1 tiết chương I-ĐỀ CHÍNH CHƯA CHIA MÃ ĐỀ.
Khối 12 (ban cơ bản)
CÂU 1 Cho hình chóp S.ABCD có đáy ABCD là hình thang có AB // CD, AB= 2a, CD = 3a, đường cao của hình thang bằng a và SA = 2a vuông góc với đáy. Khi đó, thể tích khối chóp S.ABCD bằng:
A. 	B. 	C. 	D. 
CÂU 2 Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a. Thể tích của (H) bằng:
A. 	B. 	C. 	D. 
CÂU 3 Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và chiều cao của hình chóp là . Tính theo a thể tích khối chóp S.ABC.
A. B. C. D. 
CÂU 4 Cho hình chóp S.ABCD có đáy ABCD là hình thoi có AC= a, BD = 2a, SA = 3a và SA vuông góc với đáy. Khi đó, thể tích khối chóp S.ABCD bằng:
A. 	B. 3	C. 2	D. 
CÂU 5 Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, đường cao SA vuông góc với đáy.Thể tích khối chóp S.ABC bằng . Khi đó đường cao SA bằng:
A.3a	 B.5a C.4a	 D. a
CÂU 6 Khối chóp tam giác có thể tích và chiều cao thì diện tích đáy của khối chóp bằng:
A. 	B. 	C. 	D. 
CÂU 7 Khối lăng trụ đứng có diện tích đáy 2a3 và độ dài cạnh bên có thể tích bằng:
A. 	B. 	C. 	D. 
CÂU 8 Cho khối chóp SABC có cạnh SA vuông góc mặt đáy, ABC là tam giác vuông cân tại A , SA=AB=AC=a . Thể tích của khối chóp là.
A. B. C. D. 
CÂU 9 Cho hình chóp SA BC có đáy ABC là tam giác vuông cân tại B với AC = a biết SA vuông góc với đáy ABC và SB hợp với đáy một góc 60o. Tính thể tích hình chóp
A. 	B. 	C. 	D. 
CÂU 10 Cho hình chóp đều S.ABCD gọi O là tâm của đa giác đáy ABCD,đường cao là:
A .SB B. SA C.SC D.SO
CÂU 11 Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 2a, khoảng cách từ A đến mặt
phẳng (A’BC) bằng . Khi đó thể tích lăng trụ ABC.A’B’C’ tính theo a bằng:
A. 	B. C. 	 D. 
CÂU 12 Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh . SA vuông góc với đáy. Góc giữa cạnh bên SC và mặt đáy bằng 600. Tính theo a thể tích khối chóp S.ABCD. 
A. B. C. D. 
CÂU 13 Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ xuống (ABC) là trung điểm của AB. Mặt bên (ACC’A’) tạo với đáy góc . Tính thể tích khối lăng trụ này 
A. 	B. 	 	C. 	 D. 	
CÂU 14 Diện tích của tam giác ABC vuông tại A là:
A. B. C. D. 
CÂU 15 Cho tam giác ABC vuông tại B, sinA là: 
A. B. C. D. 
CÂU 16 Cho lăng trụ đứng có đáy ABC là tam giác vuông tại B. AB = 2a, BC = a. . Tính theo a thể tích khối lăng trụ .
A. B. C. D. 
CÂU 17 Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng . Góc giữa cạnh bên và mặt đáy bằng 300.Tính theo a thể tích khối chóp S.ABCD.
A. B. C. D. 
CÂU 18 Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA =3a và SA vuông góc với đáy. Khi đó, thể tích khối chóp S.ABCD bằng:
A. 	 B. 	 C. 	 D. 
CÂU 19 Cho hình chóp đều S.ABC có cạnh bên bằng a và các mặt bên hợp với đáy một góc 450. Thể tích của khối chóp S.ABC tính theo a bằng:
A. B. C. D. 
CÂU 20 Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng . Thể tích khối chóp S.ABCD theo a và bằng
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
C
A
D
B
A
C
A
A
D
A
A
D
B
A
D
A
D
B
B