Đề kiểm tra khảo sát lớp 12 THPT môn: Toán năm 2017

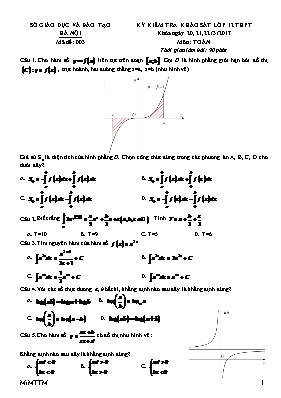
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NỘI
Mã đề: 003
KỲ KIỂM TRA KHẢO SÁT LỚP 12 THPT
Khóa ngày 20, 21,22 /3 /2017
Môn: TOÁN
Thời gian làm bài: 90 phút
Cho hàm số liên tục trên đoạn . Gọi D là hình phẳng giới hạn bởi đồ thị , trục hoành, hai đường thẳng x=a, x=b (như hình vẽ).
Giả sử S0 là diện tích của hình phẳng D. Chọn công thức đúng trong các phương án A, B, C, D cho dưới đây?
A. .	B. .
C. .	D. .
Biết rằng . Tính 
	A. T=10.	B. T=9.	C. T=5.	D. T=6.
Tìm nguyên hàm của hàm số .
	A. .	B. .
	C. .	D. .
Với các số thực dương a, b bất kì, khẳng định nào sau đây là khẳng định đúng?
	A. . B. .
	C. . D. .
Cho hàm số có đồ thị như hình vẽ:
Khẳng định nào sau đây là khẳng định đúng?
	A. .	B. .	C. .	D. .
Tìm số cạnh ít nhất của hình đa diện có 5 mặt.
	A. 9 cạnh.	B. 6 cạnh.	C. 8 cạnh.	D. 7 cạnh.
Cho mặt cầu (S) bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
	A. .	B. .	C. .	D. .
Tìm phương trình đường tiệm cận đứng của đồ thị hàm số .
	A. 	B. 	C. 	D. 
Cho hình chóp S.ABC có , , SA=SB=SC=a. Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).
	A. 	B. 	C. 	D. 
Cho hàm số liên tục trên , có đạo hàm . Hàm số đã cho có bao nhiêu điểm cực trị?
	A. Chỉ có 1 điểm cực trị.	B. Có 2 điểm cực trị.
	C. Không có cực trị.	D. Có 3 điểm cực trị.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị của các hàm số .
	A. 	B. 	C. 	D. 
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , cạnh bên SA vuông góc với mặt phẳng đáy và SA=3. Mặt phẳng qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
	A. 	B. 	C. 	D. 
Trong không gian Oxyz, cho các điểm . Tìm phương trình mặt phẳng (P) qua A, B và song song với trục hoành.
	A. 	B. 
	C. 	D. 
Hàm số đồng biến trên khoảng nào dưới đây?
	A. 	B. 	C. 	D. 
Trong không gian Oxyz, mặt phẳng (P): . Tính khoảng cách d từ điểm đến mặt phẳng (P).
	A. 	B. 	C. 	D. 
Tìm giá trị lớn nhất của hàm số trên .
	A. 	B. 	C. 	D. 
Trong không gian Oxyz, cho điểm và mặt cầu . Đường thẳng d thay đổi, đi qua điểm M, cắt mặt cầu (S) tại hai điểm A, B phân biệt. Tính diện tích lớn nhất S của tam giác OAB.
	A. 	B. 	C. 	D. 
Tìm giá trị nhỏ nhất của hàm số trên đoạn .
	A. 	B. 	C. 	D. 
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA’ và BC bằng . Tính thể tích V của khối lăng trụ ABC.A’B’C’.
	A. 	B. 	C. 	D. 
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc (m/s). Đi được 5(s), người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc (m/s2). Tính quãng đường S(m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
	A. (m).	B. (m).	C. (m).	D. (m).
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số . Tính .
	A. 	B. 
	C. 	D. 
Tìm nghiệm của phương trình .
	A. x=10.	B. x=7.	C. x=8.	D. x=9.
Hàm số nào sau đây đồng biến trên ?
	A. 	B. .	C. .	D. .
Cho hình nón có độ dài đường sinh l=2a, góc ở đỉnh của hình nón . Tính thể tích của khối nón đã cho.
	A. 	B. 	C. 	D. 
Tính tổng T tất cả các nghiệm của phương trình .
	A. T=1.	B. T=2.	C. T=8.	D. T=0.
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng .
	A. 	B. 	C. 	D. 
Trong không gian với hệ trục toạ độ Oxyz, cho ba điểm . Tìm toạ độ điểm D sao cho tứ giác ABCD là hình bình hành.
	A. 	B. 	C. 	D. 
Tìm số giao điểm n của hai đồ thị và .
	A. n=4.	B. n=2.	C. n=1.	D. n=0.
Cho hình trụ có đường cao h=5cm, bán kính đáy r=3cm. Xét mặt phẳng (P) song song với trục của hình trụ, cách trục 2cm. Tính diện tích S của thiết diện của hình trụ với mặt phẳng (P).
	A. cm2.	B. cm2.	C. cm2.	D. cm2.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Biết và Tính thể tích V của khối chóp S.ABC.
	A. 	B. 	C. 	D. 
Trong không gian Oxyz, cho mặt cầu (S): . Tính bán kính R của mặt cầu (S).
	A. 	B.	C. 	D. 
Cho hàm số liên tục trên nửa khoảng , có bảng biến thiên như hình vẽ:
x
 -3 -1 1 2
y’
y
 0 3
 -2 -5
Khẳng định nào sau đây là khẳng định đúng?
	A. Hàm số đạt cực tiểu tại 	B. 
	C. 	D. Giá trị cực tiểu của hàm số là 1.
Tìm điểm cực tiểu của hàm số .
	A. 	B. 	C. 	D. 
Hình nào sau đây không có tâm đối xứng?
	A. Tứ diện đều.	B. Hình bát diện đều.	C. Hình lập phương.	D. Hình hộp.
Cho là hàm số chẵn, có đạo hàm trên đoạn . Biết rằng và . Tính .
	A. 	B. 	C. 	D. 
Trong không gian Oxyz, cho các điểm . Tìm toạ độ tâm I của đường tròn ngoại tiếp tam giác ABC.
	A. 	B. 	C. 	D. 
Cho . Biết rằng với m, n là các số tự nhiên và tối giản. Tính .
	A. 	B. 	C. 	D. 
Trong không gian Oxyz, cho các điểm và . Mặt phẳng (P) đi qua các điểm M, N sao cho khoảng cách từ điểm B đến (P) gấp hai lần khoảng cách từ điểm A đến (P). Có bao nhiêu mặt phẳng (P) thoả mãn đề bài?
	A. Có hai mặt phẳng (P).	B. Không có mặt phẳng (P) nào.
	C. Có vô số mặt phẳng (P).	D. Chỉ có một mặt phẳng (P).
Tìm tập nghiệm S của bất phương trình .
	A. 	B. 	C. 	D. 
Tìm nguyên hàm của hàm số .
	A. 	B. 
	C. 	D. 
Hình sau là đồ thị của một trong bốn hàm số cho trong các phương án A, B, C, D. Hỏi đó là hàm nào?
	A. 	B. 	C. 	D. 
Trong không gian Oxyz, mặt cầu (S): cắt mặt phẳng theo giao tuyến là đường tròn (C). Tính diện tích S của hình tròn giới hạn bởi (C).
	A. 	B. 	C. 	D. 
Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình nghiệm đúng với mọi giá trị của ?
	A. Có 5 giá trị nguyên.	B. Có 4 giá trị nguyên.
	C. Có 7 giá trị nguyên.	D. Có 6 giá trị nguyên.
Cho hàm số có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y=4 tại điểm có hoành độ âm và đồ thị của hàm số cho bởi hình vẽ dưới đây:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
	A. 	B. 	
	C. 	D. 
Tìm tập xác định D của hàm số 
	A. 	B. 	C. 	D. 
Trong không gian Oxyz, cho mặt phẳng (P): . Vectơ nào sau đây không là vectơ pháp tuyến của mặt phẳng (P)?
	A. 	B. 	C. 	D. 
Cho Tính theo a, b.
	A. B. 	C. 	D. 
Trong không gian Oxyz, cho các điểm . Tìm toạ độ của vectơ .
	A. 	B. 	C. 	D. 
Một công ti dự kiến chi 1 tỉ đồng để sản xuất các thùng đựng sơn hình trụ có dung tích 5 lít. Biết rằng chi phí để làm mặt xung quanh của thùng đó là 100.000 đ/m2, chi phí để làm mặt đáy là 120.000 đ/m2. Hãy tính số thùng sơn tối đa mà công ti đó sản xuất được (giả sử chi phí cho các mối nối không đáng kể).
	A. 12525 thùng.	B. 58135 thùng.	C. 57582 thùng.	D. 18209 thùng.
Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất 6,5% một năm. Biết rằng, cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Tính số tiền tối thiểu x (triệu đồng, ) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng.
	A. 140 triệu đồng.	B. 154 triệu đồng.	C. 145 triệu đồng.	D. 150 triệu đồng.