Đề kiểm tra khảo sát lớp 12 môn Toán học

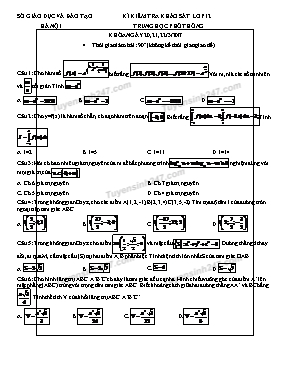
SỞ GIÁO DỤC VÀ ĐÀO TẠO KÌ KIỂM TRA KHẢO SÁT LƠP 12
 HÀ NỘI TRUNG HỌC PHỔ THÔNG
KHÓA NGÀY 20,21,22/3/2017
Thời gian làm bài: 90’ (không kể thời gian giao đề)
Câu 1: Cho hàm số biết rằng Với m,n là các số tự nhiên và tối giản. Tính 
A.
B.
C.
D.
Câu 2: Cho y=f(x) là hàm số chẵn, có đạo hàm trên đoạn . Biết rằng Tính 
A. I=2
B. I=5 
C. I=11 
D. I=14
Câu 3: Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình nghiệm đúng với mọi giá trị của 
A. Có 6 giá trị nguyên
B .Có 7 giá trị nguyên
C. Có 5 giá trị nguyên
D. Có 4 giá trị nguyên
Câu 4: Trong không gian Oxyz, cho các điểm A(1;2;-1); B(2;3;4) C(3;5;-2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC.
A.
B.
C.
D.
Câu 5: Trong không gian Oxyz cho điểm và mặt cầu . Đường thẳng d thay đổi, đi qua M, cắt mặt cầu (S) tại hai điểm A;B phân biệt. Tính diện tích lớn nhất S của tam giác OAB.
A.
B. 
C.
D.
Câu 6: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA’ và BC bằng . Tính thể tích V của khối lăng trụ ABC.A’B’C’.
A..	 B.	C.	D.
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , cạnh bên SA vuông góc với mặt đáy và SA=3. Mặt phẳng qua A và vuông góc với SC cắt các cạnh SB;SC;SD lần lượt tại các điểm M,N,P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
A.	B.	C.	 D.
Câu 8: Cho hàm số có đồ thị như hình vẽ:
Khẳng định nào sau đây đúng?
A.	B.	C.	D.
Câu 9: Hình nào sau đây không có tâm đối xứng:
Hình lập phương 	B. Hình hộp 	C. Tứ diện đều 	D. Hình bát diện đều
Câu 10: Tìm giá trị lớn nhất của hàm số trên 
A.	B.	C.	D.
Câu 11: Trong không gian Oxyz, mặt phẳng (P): . Tính khoảng cách d từ điểm M(1;-2;3) đến mặt phẳng (P).
A.	B.	C.	D.
Câu 12: Trong không gian Oxyz, mặt cầu ; cắt mặt phẳng (P): theo giao tuyến là đường tròn (C ).. Tính diện tích S của hình tròn giới hạn bởi (C ).
A.	B.	C.	D.
Câu 13: Một công ty dự kiến chi 1 tỷ đồng để sản xuất các thùng đựng sơn hình trụ có dung tích 5 lít. Biết rằng chi phí để làm mặt xung quanh của thùng đó là 100.000 đ/m2.Chi phí để làm mặt đáy là 120.000 đ/m2.Hãy tính số thùng sơn tối đa mà công ty đó sản xuất được.(Giả sử chi phí cho các mối nối không đáng kể).
A.12525 thùng 	B.18209 thùng	 C. 57582 thùng	 D. 58135 thùng.
Câu 14: Cho hình nón có độ dài đường sinh , góc ở đỉnh của hình nón . Tính thể tích V của khối nón đã cho:
A.	B.	C.	D.
Câu 15: Tìm điểm cực tiểu của hàm số 
A.	B.	 C.	D.
Câu 16: Tính diện tích S của hình phẳng giới hạn bởi đồ thị của các hàm số 
A.	B.	C.D.
Câu 17: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-1); B(2;-1;3) C(-3;5;1). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
A.D(-4;8;-3) 	B.D(-2;2;5) 	C.D(-2;8;-3) 	D.D(-4;8;-5)
Câu 18: Trong không gian với hệ trục tọa độ Oxyz, cho A(0;1;1); B(2;5;-1). Tìm phương trình mặt phẳng (P) qua A,B và song song với trục hoành.
A.	B.
C.	D.
Câu 19: Tìm nghiệm của phương trình 
A.x=7 	B.x=10 	C.x=8 	D.x=9
Câu 20: Trong không gian Oxyz, cho mặt cầu (S):. Tính bán kính R của mặt cầu (S).
A.R=3 	B.	C.R=9 D.
Câu 21: Trong không gian Oxyz, cho các điểm A(-1;2;-3); B( 2;-1;0). Tìm tọa độ của vecto .
A.	B.	C.	D.
Câu 22: Hàm số nào sau đây đồng biến trên R?
A.	B.	C.	D.
Câu 23: Cho mặt cầu (S) bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
A.	B.h=R	C.	D.
Câu 24: Biết rằng .Tính 
A.T=9 	B.T=10 	C.T=5	D.T=6
Câu 25: Hình bên là đồ thị của một trong bốn hàm số cho trong các phương án A;B;C;D, hỏi đó là hàm số nào:
A.	B.	C.	D.
Câu 26: Tìm tập xác định D của hàm số 
A.	B.	C.	D.D=R
Câu 27: Tìm giá trị nhỏ nhất của hàm số trên đoạn [-3;2].
A. 
B. 
C. 
D. 
Câu 28: Trong không gian Oxyz, cho các điểm A(1;0;0), B(-2;0;3), M(0;0;1) và N(0;3;1). Mặt phẳng (P) đi qua các điểm M, N sao cho khoảng cách từ điểm B đến (P) gấp hai lần khoảng cách từ điểm A đến (P). Có bao nhiêu mặt phẳng (P) thỏa mãn đề bài?
A. Có hai mặt phẳng (P).
B. Không có mặt phẳng (P) nào.
C. Có vô số mặt phẳng (P).
D. Chỉ có một mặt phẳng (P).
Câu 29: Trong không gian Oxyz, cho mặt phẳng (P): x – z – 1 = 0. Veto nào sau đây không là vecto pháp tuyến của mặt phẳng (P)?
A. 
B. 
C. 
D. 
Câu 30: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh A. Biết và . Tính thể tích V của khối chóp S.ABC. 
A. .
B. 
C. 
D. 
Câu 31: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc . Đi được 5 (s), người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc . Tính quãng đường S(m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
A. S = 94,00 (m)
B. S = 96,25 (m)
C. S = 87,50 (m)
D. S = 95,70 (m)
Câu 32: Tìm số giao điểm n của hai đồ thị và.
A. n = 0
B. n = 1
C. n = 4
D. n = 2
Câu 33: Cho . Tính theo a, b
A.	
B.
C. 	
D. 
Câu 34: Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Tính M + m.
A. B. 
C. 
D. 
Câu 35: Với các số thực dương a, b bất kì. Khẳng định nào sau đây là khẳng định đúng?
A. 
B. 
C. 
D. 
Câu 36: Tìm phương trình đường tiệm cận đứng của đồ thị hàm số .
A. y = 2.
B. x = 1.
C. y = 1.
D. x = -1.
Câu 37: Cho hàm số liên tục trên nửa khoảng [-3;2), có bảng biến thiên như hình vẽ:
Khẳng định nào sau đây là khẳng định đúng?
A. 
B. 
C. Giá trị cực tiểu của hàm số là 1.
D. Hàm số đạt cực tiểu tại x = -1.
Câu 38: Tìm nguyên hàm của hàm số 
A. 	
B. 
C. 
D. 
Câu 39: Tìm nguyên hàm của số 
A. 
B. 
C. 
D. 
Câu 40: Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất 6,5% một năm. Biết rằng, cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Tính số tiền tối thiểu x (triệu đồng, ) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy giá trị 30 triệu đồng.
A. 150 triệu đồng.
B. 154 triệu đồng.
C. 145 triệu đồng.
D. 140 triệu đồng.
Câu 41: Cho hàm số liên tục trên ℝ, có đạo hàm Hàm số đã cho có bao nhiêu điểm cực trị?
A. Có 3 điểm cực trị.
B. Không có cực trị.
C. Chỉ có 1 điểm cực trị.
D. Có 2 điểm cực trị.
Câu 42: Cho hình chóp S.ABC có Tính khoảng cách d từ A đến mặt phẳng (SBC).
A. 
B. 
C. 
D. 
Câu 43: Cho hàm số có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và có đồ thị của hàm số cho bởi hình vẽ dưới đây:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
A. 
B. 
C. 
D. 
Câu 44: Hàm số đồng biến trên khoảng nào dưới đây?
A. 
B. 
C. 
D. 
Câu 45: Tính tổng T tất cả các nghiệm của phương trình .
A. T = 0.
B. T = 2.
C. T = 1.
D. T = 8.
Câu 46: Tìm tập nghiệm S của bất phương trình 
A. 
B. 
C. 
D. 
Câu 47: Cho hình trụ có đường cao h = 5cm, bán kính đáy r = 3cm. Xét mặt phẳng (P) song song với trục của hình trụ, cách trục 2cm. Tính diện tích S của thiết diện của hình trụ với mặt phẳng (P).
A. 
B. 
C. 
D. 
Câu 48: Cho hàm số liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị , trục hoành, hai đường thẳng x = a, x = b ( như hình vẽ dưới đây).
Giả sử SD là diện tích của hình phẳng D. Chọn công thức đúng trong các phương án A, B, C, D cho dưới đây?
A. 
B. 
C. 
D. 
Câu 49: Tìm số cạnh ít nhất của hình đa diện có 5 mặt.
A. 6 cạnh.
B. 7 cạnh.
C. 8 cạnh.
D. 9 cạnh.
Câu 50: Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng (-2;0).
A. 
B. 
C. 
D. 
HƯỚNG DẪN GIẢI CHI TIẾT
Thực hiện: Ban chuyên môn Tuyensinh247.com
1D
2D
3C
4A
5D
6C
7C
8C
9C
10B
11D
12A
13D
14A
15B
16C
17A
18B
19D
20A
21D
22D
23C
24B
25C
26A
27B
28C
29C
30A
31B
32D
33C
34A
35B
36B
37
38B
39A
40C
41D
42D
43B
44C
45B
46A
47B
48A
49C
50A
Câu 1:
Ta có:
Chọn D.
Câu 2
– Cách giải
Do f(x) là hàm chẵn nên f(-2x)=f(2x), suy ra
Đặt 
Hay 
Chọn D
Câu 3
Phương pháp:
Ta có 
Lời giải:
Đặt , khi đó bất phương trình đã cho có dạng 
Yêu cầu bài toán trở thành tìm các giá trị nguyên của m để bất phương trình nghiệm đúng với mọi giá trị của t.
Ta có để bất phương trình nghiệm đúng với mọi giá trị của t thì 
Suy ra các giá trị nguyên của m là -4, -3, -2, -1, 0
Đáp án C.
Câu 4.
Phương pháp:
Tâm đường tròn ngoại tiếp tam giác thì cách đều các đỉnh của tam giác đó
Lời giải:
Gọi I(x;y;z). Khi đó ta có 
Với 
Phương trình mặt phẳng đi qua điểm A và có vtpt là 
Mặt khác từ 
Từ (1) và (2) ta có hệ phương trình 
Đáp án A.
Mặt cầu đã cho có tâm O(0;0;0) và bán kính 
Có nên M nằm trong mặt cầu
Khi đó diện tích AOB lớn nhất khi OM ⊥ AB. Khi đó và 
Chọn đáp án D
Câu 6.
Phương pháp:
 Thể tích khối lăng trụ trong đó B là diện tích đáy, h là chiều cao
Khoảng cách giữa hai đường thẳng là độ dài đường vuông góc chung của hai đoạn thẳng đó.
Lời giải:
Gọi M là trung điểm của BC. Từ M kẻ MK vuông góc với AA’.
Ta có MK vuông góc AA’, MK vuông góc với BC ( vì 
Vậy khoảng cách giữa AA’ với BC là MK.
Diện tích tam giác đều cạnh a là 
Xét tam giác ABC có 
Ta có
Thể tích lăng trụ 
Đáp án C
Câu 7
Ta chứng minh được ∆ AMN vuông tại M và ∆ APN vuông tại P
⇒ Trục của đường tròn ngoại tiếp tứ giác AMNP là đường thẳng trung trực của AN trong mặt phẳng (SAC)
⇒ O là tâm mặt cầu ngoại tiếp chóp C.AMNP
⇒ Bán kính mặt cầu ngoại tiếp C.MNP là 
Thể tích mặt cầu đó là 
Chọn đáp án C
Câu 8
Đồ thị hàm số đã cho có tiệm cận đứng nên c, d cùng dấu
Đồ thị hàm số đã cho có tiệm cận ngang nên a,c cùng dấu
⇒ ad > 0
Đồ thị hàm số đã cho cắt Oy tại là điểm có tung độ âm nên b, d trái dấu
⇒ bc < 0
Chọn đáp án C
Câu 9
–Cách giải.
Hình tứ diện đều không có tâm đối xứng
Chọn C
Câu 10
–Phương pháp
Tìm giá trị lớn nhất (nhỏ nhất) của hàm số trên 1 đoạn [a;b]
+ Tính y’, tìm các nghiệm x1, x2, ... thuộc [a;b] của phương trình y’ = 0
+ Tính y(a), y(b), y(x1), y(x2), ...
+ So sánh các giá trị vừa tính, giá trị lớn nhất trong các giá trị đó chính là GTLN của hàm số trên [a;b], giá trị nhỏ nhất trong các giá trị đó chính là GTNN của hàm số trên [a;b]
– Cách giải
Câu 10
–Phương pháp
Tìm giá trị lớn nhất (nhỏ nhất) của hàm số trên 1 đoạn [a;b]
+ Tính y’, tìm các nghiệm x1, x2, ... thuộc [a;b] của phương trình y’ = 0
+ Tính y(a), y(b), y(x1), y(x2), ...
+ So sánh các giá trị vừa tính, giá trị lớn nhất trong các giá trị đó chính là GTLN của hàm số trên [a;b], giá trị nhỏ nhất trong các giá trị đó chính là GTNN của hàm số trên [a;b]
– Cách giải
Chọn B
Câu 11
– Cách giải
Chọn D
Câu 12
– Cách giải
 (S) có tâm I(1;-2;0) bán kính R=3
Gọi H là tâm đường tròn ta có , Gọi M là một điểm thuộc đường tròn thì 
Chọn A
Câu 13
– Cách giải
Gọi R là bán kính đường tròn đáy có 
Số tiền làm mặt xung quanh là :
Số tiền làm hai mặt đáy 
Số tiền làm một hộp là 
Số thùng nhiều nhất có thể làm là 
Chọn đáp án D
Câu 14
- Cách giải:
Chọn A
Câu 15
– Cách giải.
Chọn B
Câu 16: 
Phương pháp: Nắm vững công thức tính diện tích hình phẳng giới hạn bởi 2 đường y = f(x) và y = g(x). Trước hết ta giải phương trình f(x) – g(x) = 0, thu được các nghiệm a, b, c,d ta lấy 2 nghiệm nhỏ nhất và lớn nhất, giả sử là a và b thì diện tích cần tính là: .
Lời giải:
Ta có: 
Chọn C.
Câu 17: 
Phương pháp: Để tứ giác ABCD là hình bình hành thì ta cần giải 1 trong 2 phương tình sau: .
Lời giải: 
Ta có: x=-4;y=8,z=-3 , D(-4;8;-3)
Chọn A
Câu 18:
Phương pháp: (P) // Ox thì (P) sẽ có 1 vectơ chỉ phương là (1; 0; 0). Ta sẽ dựa vào việc P qua AB để tìm ra vectơ chỉ phương thứ 2 là . Qua đó viết được vectơ pháp tuyến của (P) là và từ đó có được mặt (P).
Lời giải:
Ta có: 
.
Chọn B.
Câu 19: 
Ta có: 
Chọn D.
Câu 20:
Phương pháp: Ta nhớ lại công thức mặt cầu tâm I(a; b; c) và bán kính R là:.
Lời giải:
Ta có phương trình đã cho tương đương với: 
Chọn A.
Câu 21:
Phương pháp: Ta nhớ công thức: 
Lời giải:
Chọn D.
Câu 22:
Phương pháp: Để hàm số đồng biến trên R thì ( dấu “ = “ chỉ xảy ra ở hữu hạn điểm). Tuy nhiên ta sẽ nhớ với các hàm số mũ là logarit thì:
Hàm đồng biến trên R khi và chỉ khi 
Lời giải:
Ý A là , ý B thì là hàm đống biến nên nghịch biến trên R.
 Do vậy hàm này đồng biến trên .
Chọn D.
Câu 23:
Phương pháp: Áp dụng công thức khi mặt trụ nội tiếp mặt cầu thì: 
Lời giải:
Ta có: Khi mặt trụ nội tiếp mặt cầu thì: .
Diện tích xung quanh hình trụ: 
Áp dụng BĐT Cô Si ta có: 
Dấu “ = “ xảy ra khi và chỉ khi nên: 
Chọn C.
Câu 24:
Để tính ta sẽ đổi cận như sau: 
Đặt 
Như vậy ta có: Chọn B.
Câu 25:
Nhìn vào dạng đồ thị ta thấy ngay đây là đồ thị của hàm trùng phương 
Nhìn vào hình dạng của đồ thị thì ta sẽ thấy sự biến thiên là giảm tăng giảm tăng tương ứng với dấu - + - + trong bảng biến thiên.
Như vậy hệ số của phải > 0 thì với 3 nghiệm phân biệt của phương trình f’(x) = 0 ta sẽ có bảng dấu như vậy.
Các bạn tự suy luận hệ số < 0 thì sẽ có ngược lại.
Chọn C.
Câu 26: 
Ta có hàm số xa với a không nguyên có TXĐ là (0;+∞)
Chọn A.
Câu 27: 
Phương pháp: Để tìm GTLN, GTNN của hàm số y = f(x) trên [a; b] ta lần lượt tìm GTLN hoặc GTNN của các giá trị f(a), f(b) và với là toàn bộ nghiệm của phương trình f’(x) = 0 trên đoạn đã cho.
Lời giải:
.
Do đó giá trị nhỏ nhất cần tìm là – 1.
Chọn B.	
Câu 28:
Có nên M ∈ đoạn AB và AB = 3AM ⇒ BM = 2AM
Ta thấy N ∉ AB nên mọi mặt phẳng qua MN và không chứa A, B đều thỏa mãn đề bài
Vậy có vô số mặt phẳng thỏa mãn
Chọn đáp án C
Câu 29: 
Phương pháp: Vectơ pháp tuyến của mặt phẳng (P) ax + by + cz + d = 0 là (a; b; c). Thi k. cũng là vecto pháp tuyến của mặt phẳng (P)
Lời giải: Dễ có vectơ pháp tuyến của mặt phẳng cần tìm là (1; 0; -1). Nên đáp án A,B,D đúng.
Chọn C.
Câu 30:
Phương pháp: Tam giác đều cạnh a có độ dài đường cao là và công thức thể tích hình chóp .
Lời giải:
Ta có:
Chọn A.
Câu 31
– Phương pháp:
+ Dựng đồ thị hàm số v theo t
+ Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số đó và trục hoành
– Cách giải
Từ khi bắt đầu phanh đến khi dừng lại ô tô đi thêm được khoảng thời gian là 
Ta có đồ thị vận tốc xe theo thời gian như hình bên
Quãng đường đi được của xe bằng diện tích tam giác có đáy 5,5 (s) và chiều cao 35 (m/s) nên có giá trị bằng: 
Chọn đáp án B
Câu 32
– Phương pháp
Số giao điểm của hai đồ thị hàm số y = f(x) và y = g(x) là số nghiệm của phương trình 
f(x) = g(x)
– Cách giải
Xét phương trình hoành độ giao điểm của 2 đồ thị hàm số:
Phương trình này có 2 nghiệm nên 2 đồ thị hàm số cắt nhau tại 2 điểm. Vậy n = 2
Chọn đáp án D
Câu 33
– Phương pháp
Dùng phép biến đổi logarit đưa về logarit cùng cơ số
– Cách giải
Chọn đáp án C
Câu 34
– Phương pháp
Tính y’ và khảo sát hàm số trên TXĐ để tìm GTLN, GTNN của hàm số.
– Cách giải
TXĐ: [1;5]
Có 
Có 
Chọn đáp án A
Câu 35
log(ab) = log a + log b
Chọn đáp án B
Câu 36
– Phương pháp
Đồ thị hàm số với ad ≠ bc thì có tiệm cận đứng 
– Cách giải
Đồ thị hàm số đã cho có tiệm cận đứng x = 1
Chọn đáp án B
Câu 37
Không có đáp án đúng
Câu 38
– Phương pháp
Sử dụng công thức nguyên hàm hợp
– Cách giải
Chọn đáp án B
Câu 39
– Phương pháp
Sử dụng công thức nguyên hàm hợp
– Cách giải
Chọn đáp án A
Câu 40
– Phương pháp
Công thức lãi kép: Với A0 là số tiền gửi ban đầu, r% là lãi suất hàng năm, sau n năm cả vốn lẫn lãi người đó có là 
– Cách giải
Nếu ban đầu ông Việt gửi x triệu đồng thì sau 3 năm số tiền lãi của ông có là 
Để số tiền này đủ mua chiếc xe máy thì 
Mà x là tối thiểu nên x = 145
Chọn đáp án C
Câu 41
– Phương pháp
Số điểm cực trị của hàm số đã cho là số nghiệm của f ‘(x) mà qua nghiệm đó f ‘(x) đổi dấu
– Cách giải
 nên f ‘(x) có 3 nghiệm x = 0; x = 1 và x = –1 và f ‘(x) đổi dấu khi qua 2 nghiệm x = 0 và x = –1; không đổi dấu khi qua nghiệm x = 1 (vì số mũ của x – 1 là chẵn)
Vậy đồ thị hàm số đã cho có 2 cực trị
Chọn đáp án D
Câu 42
Gọi M là trung điểm AC.
Ta có ∆ SAC vuông cân tại S nên SM ⊥ AC và 
Ta có ∆ SAB và ∆ SBC đều nên AB = BC = a, suy ra ∆ ABC vuông cân tại B
Suy ra 
Suy ra ∆ SMB vuông cân tại M
⇒ SM ⊥ MB
⇒ SM ⊥ (ABC) 
Chọn đáp án D
Câu 43
– Phương pháp
Tìm f ‘(x), tìm f(x) rồi dùng công thức diện tích hình thang cong.
– Cách giải
Đồ thị hàm số y = f’(x) là đồ thị hàm số bậc hai, nhận Oy làm trục đối xứng nên 
f ‘(x) = ax2 + c
Đồ thị hàm số y = f’(x) đi qua (0;–3); (–1;0) và (1;0) nên c = –3; a = 3
Dễ thấy đồ thị hàm số y = f(x) đạt cực trị tại x = ±1
Vì y = f(x) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm nên f (–1) = 4
⇒ f(x) = x3 – 3x + 2
Có f(x) giao Ox tại x = –2 và x = 1
Diện tích hình phẳng cần tính là 
Chọn đáp án B
Câu 44
Hàm số y = x4 – 1 là parabol có bề lõm quay lên trên nên đồng biến trên (0;+∞)
Chọn đáp án C
Câu 45
– Phương pháp
Đặt ẩn phụ sử dụng định lý Viét cho phương trình bậc 2
– Cách giải
Đặt phương trình đã cho trở thành . Vì ∆’ = 42 – 4 = 12 > 0 nên phương trình đó có 2 nghiệm t1, t2 thỏa mãn với x1, x2 là 2 nghiệm của phương trình đã cho
Vậy phương trình đã cho có 2 nghiệm có tổng bằng 2
Chọn đáp án B
Câu 46
– Phương pháp
Tìm điều kiện xác định rồi giải phương trình
– Cách giải
Điều kiện: 
Với điều kiện trên bất phương trình đã cho tương đương với 
Kết hợp điều kiện ta có nghiệm của bất phương trình là 
Chọn đáp án A
Câu 47
– Phương pháp
Xác định chiều dài và chiều rộng của thiết diện
– Cách giải
Gọi AB là giao của (P) với hình tròn đáy (O) của hình trụ. Gọi H là trung điểm AB. Ta có OH ⊥ AB; OH = 2cm; OA = OB = 3cm
Thiết diện thu được là hình chữ nhật có các kích thước là và h = 5cm nên có diện tích 
Chọn đáp án B
Câu 48
Ta thấy f(x) 0 với x ∈ (0;b) nên 
Chọn đáp án A
Câu 49
– Phương pháp
Mỗi mặt của đa diện phải có ít nhất 3 cạnh và mỗi cạnh của đa diện là cạnh chung của 2 mặt nên số cạnh của đa diện n mặt không nhỏ hơn 
– Cách giải
Với đa diện 5 mặt thì số cạnh của nó không nhỏ hơn 
⇒ Đa diện 5 mặt có ít nhất 8 cạnh
(Lấy ví dụ hình chóp tứ giác)
Chọn đáp án C
Câu 50
– Phương pháp
Tìm điều kiện của m để hàm số đồng biến trên khoảng (a;b):
+ Lập bất phương trình y’ ≥ 0
+ Cô lập m đưa về phương trình 
+ Khảo sát hàm số f(x) trên (a;b) để tìm m
– Cách giải
Có 
Với x ∈ (–2;0) ta có 
Có 
Vậy tất cả các giá trị m cần tìm là 
Chọn đáp án A