Đề kiểm tra học kỳ II môn Toán Lớp 7 - Đề 1 - Năm học 2011-2012 - Trường THCS Vinh Giang (Có đáp án)

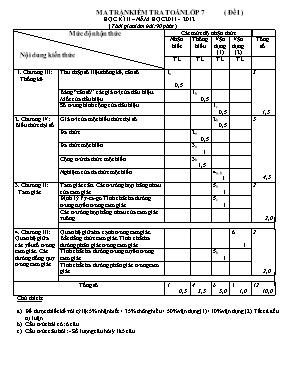
 MA TRẬN KIỂM TRA TOÁN LỚP 7 ( Đề I )
HỌC KÌ II – NĂM HỌC 2011 - 2012
 (Thời gian làm bài: 90 phút )
 Mức độ nhận thức
 Nội dung kiến thức
Các mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng(1)
 Vận dụng
 (2) 
Tổng số 
TL
TL
TL
TL
1. Chương III:
 Thống kê
Thu thập số liệu thống kê, tần số
1a
 0,5
3
 1,5
Bảng “tần số” các giá trị của dấu hiệu. Mốt của dấu hiệu
1b
 0,5
Số trung bình cộng của dấu hiệu
1c
 0,5
2. Chương IV:
Biểu thức đại số
Giá tri của một biểu thức đại sô
2b
 0,5
5
 4,5
Đa thức
2a
 0,5
Đa thức một biến
3a
 1 
Cộng trừ đa thức một biến
3b
 1,5
Nghiệm của đa thức một biến
4a, b
 1
3. Chương II:
 Tam giác
Tam giác cân. Các trường hợp bằng nhau của tam giác
5a
 1
2
 2,0
Định lý Py-ta-go. Tính chất ba đường trung tuyến trong tam giác
5c
 1
Các trường hợp bằng nhau của tam giác vuông
4. Chương III:
Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác 
Quan hệ giữa ba cạnh trong tam giác. Bất đẳng thức tam giác. Tính chất ba đường phân giác trong tam giác
6
 1
2
 2,0
Tính chất ba đường trung tuyến trong tam giác
5b
 1
Tính chất ba đường phân giác trong tam giác
Tổng sô
1
 0,5
4
 3,5
6
 5,0
1
 1,0
12
 10,0
Chú thích: 
Đề được thiết kế với tỷ lệ: 5% nhận biết + 35% thông hiểu + 50% vận dụng(1)+ 10% vận dụng (2). Tất cả đều tự luận.
Cấu trúc bài có: 6 câu
Cấu trúc câu hỏi: - Số lượng câu hỏi ý là 5 câu
PHÒNG GD&ĐT HUYỆN PHÚ LỘC	KIỂM TRA HỌC KÌ II NĂM HỌC 2011 - 2012 
TRƯỜNG THCS VINH GIANG MÔN : TOÁN - LỚP 7
 Thời gian làm bài: 90 phút	
ĐỀ CHÍNH THỨC ( Đề1)
.
Câu1: (1,5đ)
 Điểm kiểm tra 1 tiết môn toán của lớp 7A được bạn lớp trưởng ghi lại như sau
5
8
4
8
6
6
5
7
4
3
6
7
7
3
8
6
7
6
5
9
7
9
7
4
4
7
10
6
7
5
4
7
6
5
2
8
Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
Lập bảng “tần số” và tìm Mốt của dấu hiệu.
Tính số trung bình cộng của dấu hiệu.
Câu2: (1đ)
 Cho đa thức M = 6 x6y + x4y3 – y7 – 4x4y3 + 10 – 5x6y + 2y7 – 2,5.
Thu gọn và tìm bậc của đa thức.
Tính giá trị của đa thức tại x = -1 và y = 1.
Câu3: (2,5)
 Cho hai đa thức:
 P(x) = x2 + 5x4 – 3x3 + x2 + 4x4 + 3x3 – x + 5
 Q(x) = x - 5x3– x2 – x4 + 4x3 - x2 + 3x – 1
Thu gọn rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.
Tính P(x) + Q(x) và P(x) - Q(x) 
Câu4: (1đ)
Tìm nghiệm của các đa thức 
 a. R(x) = 2x + 3 b. H(x) = (x – 1)( x+ 1)
Câu5: (3đ)
 Cho ABC cân tại A ( A nhọn ). Tia phân giác góc của A cắt BC tại I.
 a. Chứng minh AI BC.
 b. Gọi D là trung điểm của AC, M là giao điểm của BD với AI. Chứng minh rằng M là trọng tâm của tâm giác ABC.
 c. Biết AB = AC = 5cm; BC = 6 cm. Tính AM.
Câu6: (1đ)
 Trên tia phân giác góc A của tam giác ABC ( AB > AC) lấy điểm M.
 Chứng minh MB - MC < AB – AC
 .. Hết .
PHÒNG GD&ĐT HUYỆN PHÚ LỘC	KIỂM TRA HỌC KÌ II NĂM HỌC 2011 - 2012 
TRƯỜNG THCS VINH GIANG MÔN : TOÁN - LỚP 7
ĐỀ CHÍNH THỨC
ĐÁP ÁN VÀ THANG ĐIỂM
( Đáp án này gồm 02 trang )
Câu
Ý
Nội dung
Điểm
1
a
b
c
- Dấu hiệu ở đây là điểm kiểm tra toán một tiết của mỗi học sinh
- Số các giá trị là : N = 36
Bảng tần số:
Giá trị (x)
2
3
4
5
6
7
8
9
10
Tần số (n)
1
2
5
5
7
9
4
2
1
N = 36
 M0 = 7
 X = 
0,5
0,5
0,5
2
a
b
- Thu gọn đa thức ta được: M = y7 + x6y - x4y3 + 7,5 ; đa thức có bậc 7
- Thay x = -1 và y = 1 vào đa thức ta được :
 M(-1; 1) = 17 + (-1)6.1 - (-1)4.13 + 7,5 = 1 + 1 - + 7,5 = 
0,5
0,5
3
a
b
- Thu gọn rồi săp xếp theo lũy thừa giảm dần của biến, ta được:
 P(x) = x2 + 5x4 - 3x3 + x2 + 4x4 + 3x3 - x + 5 = 9x4 + 2 x2 - x + 5
 Q(x) = x - 5x3 - x2 - x4 + 4x3 - x2 + 3x - 1= - x4 - x3 - 2x2 + 4x - 1
P(x) + Q(x) = 8x4 - x3 + 3x + 4
P(x) - Q(x) = 10 x4 - x3 + 4x2 - 5x + 6
1
0,75
0,75
4
a
b
Tìm được nghiệm của đa thức a. R(x) = 2x + 3 là x = 
 b. H(x) = (x – 1)( x+ 1) là x = 1 và x = -1 
0,5
0,5
5
a
b
c
- Vẽ hình đúng và ghi GT, KL đúng .
- Chứng minh được AIB = AIC (cgc) => I1 = I2 ( Hai góc tương ứng)
 Mà I1 + I2 = 1800 ( Hai góc kề bù) => I1 = I2 = 900 => AI BC . đpcm
- Ta có DA = DC => BD là đường trung tuyến ứng với cạnh AC.
Trong tam giác cân ABC ( cân tại A), AI là đường phân giác ứng với đáy BC => AI cũng là đường trung tuyến 
=> M là giao của AI và BD nên M là trọng tâm của tam giác ABC ( Tính chất ba đường trung tuyến của tam giác) đpcm
Trong tam giác cân ABC ( Cân tại A), AI là phân giác cũng là trung tuyến => IB = IC = BC
=> IB = IC = 3 (cm)
Áp dụng định lí Py-ta-go vào tam giác vuông AIB, ta có: AI2 = AB2 – IB2 = 52 – 32 = 16
 => AI = 4 (cm)
M là trọng tâm của tam giác ABC => AM = AI = . 4 = 8/3 (cm)
0,5
0,5
0,5
0,5
6
- kẻ MI vuông góc với AB; MJ vuông góc với AC => MI = MJ (1) ( Tính chất tia phân giác của góc)
- Ta lại có AB – AC = AI + IB – ( AJ + JC) => AB – AC = IB – JC (2) ( hai tam giác vuông AIM và AJM bằng nhau ( ch-gn) => AI = AJ).
- Trên tia IB lấy điểm C’ sao cho IC’ = JC. Từ (2) suy ra AB – AC = IB – IC’ = C’B (3)
Trong tam giác BMC’, ta có C’B > BM – MC’ ( BĐT tam giác) (4)
- Măt khác ta có MIC’ = MJC (cgc) => MC’ = MC (5).
Từ (3), (4) và (5) suy ra AB – AC > MB - MC đpcm
0,25
0,25
0,25
0,25
 MA TRẬN KIỂM TRA TOÁN LỚP 7 ( Đề II )
HỌC KÌ II – NĂM HỌC 2011 - 2012
 (Thời gian làm bài: 90 phút )
 Mức độ nhận thức
 Nội dung kiến thức
Các mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng(1)
 Vận dụng
 (2) 
Tổng số 
TL
TL
TL
TL
1. Chương III:
 Thống kê
Thu thập số liệu thống kê, tần số
1a
 0,5
3
 1,5
Bảng “tần số” các giá trị của dấu hiệu. Mốt của dấu hiệu
1b
 0,5
Số trung bình cộng của dấu hiệu
1c
 0,5
2. Chương IV:
Biểu thức đại số
Giá tri của một biểu thức đại sô
2b
 0,5
5
 4,5
Đa thức
2a
 0,5
Đa thức một biến
3a
 1 
Cộng trừ đa thức một biến
3b
 1,5
Nghiệm của đa thức một biến
4a, b
 1
3. Chương II:
 Tam giác
Tam giác cân. Các trường hợp bằng nhau của tam giác
5a
 1
2
 2,0
Định lý Py-ta-go. Tính chất ba đường trung tuyến trong tam giác
5c
 1
Các trường hợp bằng nhau của tam giác vuông
4. Chương III:
Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác 
Quan hệ giữa ba cạnh trong tam giác. Bất đẳng thức tam giác. Tính chất ba đường phân giác trong tam giác
6
 1
2
 2,0
Tính chất ba đường trung tuyến trong tam giác
5b
 1
Tính chất ba đường phân giác trong tam giác
Tổng sô
1
 0,5
4
 3,5
6
 5,0
1
 1,0
12
 10,0
Chú thích: 
Đề được thiết kế với tỷ lệ: 5% nhận biết + 35% thông hiểu + 50% vận dụng(1)+ 10% vận dụng (2). Tất cả đều tự luận.
Cấu trúc bài có: 6 câu
Cấu trúc câu hỏi: - Số lượng câu hỏi ý là 5 câu
PHÒNG GD&ĐT HUYỆN PHÚ LỘC	KIỂM TRA HỌC KÌ II NĂM HỌC 2011 - 2012 
TRƯỜNG THCS VINH GIANG MÔN : TOÁN - LỚP 7
 Thời gian làm bài: 90 phút	
ĐỀ CHÍNH THỨC ( Đề2)
.
Câu1: (1,5đ)
 Thời gian ( Tính bằng phút) giải một bài toán của học sinh lớp 7A được thầy giáo bộ môn ghi lại như sau
4
8
4
8
6
6
5
7
5
3
6
7
7
3
6
5
6
6
6
9
7
9
7
4
4
7
10
6
7
5
4
6
6
5
4
8
Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
Lập bảng “tần số” và tìm Mốt của dấu hiệu.
Tính số trung bình cộng của dấu hiệu.
Câu2: (1đ)
 Cho đa thức M = 3x6y + x4y3 – 4y7 – 4x4y3 + 11 – 5x6y + 2y7 - 2.
Thu gọn và tìm bậc của đa thức.
Tính giá trị của đa thức tại x = 1 và y = -1.
Câu3: (2,5)
 Cho hai đa thức:
 R(x) = x2 + 5x4 – 2x3 + x2 + 6x4 + 3x3 – x + 15
 H(x) = 2x - 5x3– x2 – 2 x4 + 4x3 - x2 + 3x – 7
Thu gọn rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.
Tính R(x) + H(x) và R(x) - H(x) 
Câu4: (1đ)
Tìm nghiệm của các đa thức 
 a. P(x) = 5x - 3 b. F(x) = (x +2)( x- 1)
Câu5: (3đ)
 Cho ABC cân tại A ( A nhọn ). Tia phân giác góc của A cắt BC tại I.
 a. Chứng minh AI BC.
 b. Gọi M là trung điểm của AB, G là giao điểm của CM với AI. Chứng minh rằng BG là đường trung tuyến của tam giác ABC.
 c. Biết AB = AC = 15cm; BC = 18 cm. Tính GI.
Câu6: (1đ)
 Cho đoạn thẳng AB. Gọi d là đường trung trực của AB. Trên đường thẳng d lấy điểm M bất kì. Trong mặt phẳng lấy đểm C sao cho BC < CA.
So sánh MB + MC với CA.
Tìm vị trí của M trên d sao cho MB + MC nhỏ nhất.
 .. Hết .
PHÒNG GD&ĐT HUYỆN PHÚ LỘC	KIỂM TRA HỌC KÌ II NĂM HỌC 2011 - 2012 
TRƯỜNG THCS VINH GIANG MÔN : TOÁN - LỚP 7
ĐỀ CHÍNH THỨC
 ĐÁP ÁN VÀ THANG ĐIỂM (Đề 2)
( Đáp án này gồm 02 trang )
Câu
Ý
Nội dung
Điểm
1
a
b
c
- Dấu hiệu ở đây là thời gian ( tính bằng phút) giải một bài toán toán của mỗi học sinh
- Số các giá trị là : N = 36
Bảng tần số:
Giá trị (x)
3
4
5
6
7
8
9
10
Tần số (n)
2
6
5
10
7
3
2
1
N = 36
 M0 = 6
 X = 
0,5
0,5
0,5
2
a
b
- Thu gọn đa thức ta được: M = - 2y7 - 2x6y -x4y3 + 9 ; đa thức có bậc 7
- Thay x = 1 và y = -1 vào đa thức ta được :
 M(1; -1) = -2.17 -2 .16.(-1) - 14.(-1)3 + 9 = -2 +2 ++9  = 12,5
0,5
0,5
3
a
b
- Thu gọn rồi săp xếp theo lũy thừa giảm dần của biến, ta được:
 R(x) = x2 + 5x4 – 2x3 + x2 + 6x4 + 3x3 – x + 15 = 11x4 + x3 +2x2 – x + 15
 H(x) = 2x - 5x3– x2 – 2 x4 + 4x3 - x2 + 3x – 7 = -2x4 - x3 -2x2 + 5x - 7
R(x) + H(x) = 9x4 + 4x +8
R(x) - H(x) = 13x4 + 2x3+ 4x2 – 6x + 22
1
0,75
0,75
4
a
b
Tìm nghiệm của các đa thức 
a. P(x) = 5x - 3 có nghiệm 5x - 3 = 0 x = 
b. F(x) = (x +2)( x- 1) có nghiệm (x +2)( x- 1) = 0 (x +2) = 0 hoặc 
( x- 1) =0 x= -2 hoặc x = 1
0,5
0,5
5
a
b
c
- Vẽ hình đúng và ghi GT, KL đúng .
- Chứng minh được AIB = AIC (cgc) => I1 = I2 ( Hai góc tương ứng)
 Mà I1 + I2 = 1800 ( Hai góc kề bù) => I1 = I2 = 900 => AI BC . đpcm
- Ta có MA = MB => CM là đường trung tuyến ứng với cạnh AB.
Trong tam giác cân ABC ( cân tại A), AI là đường phân giác ứng với đáy BC => AI cũng là đường trung tuyến 
=> G là giao của AI và CM nên G là trọng tâm của tam giác ABC ( Tính chất ba đường trung tuyến của tam giác) => BG là đường trung tuyến của tam giác ABC. đpcm
- Trong tam giác cân ABC ( Cân tại A), AI là phân giác cũng là trung tuyến => IB = IC = BC => IB = IC = 9 (cm)
- Áp dụng định lí Py-ta-go vào tam giác vuông AIB, ta có: AI2 = AB2 – IB2 = 152 – 92 = 144
 => AI = 12 (cm)
G là trọng tâm của tam giác ABC => GI = AI = . 12 = 4 (cm) 
0,5
0,5
0,5
0,5
0,5
0,5
6
a
b
- M 0 d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có :
 MA + MC > AC. Vậy MB + MC > AC
 Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H. 
 Vậy khi M H thì : MB + MC = HB + HC = HA + HC
 => MB + MC = AC
Vậy ta có MB + MC ≥ AC
- Khi M trùng với H thì HB + HC = AC. 
Tức là MB + MC nhỏ nhất khi M H giao điểm của AC với d. 
0,25
0,25
0,25
0,25