Đề kiểm tra học kỳ 2 môn: Toán 7 - Trường THCS Tô Hiệu

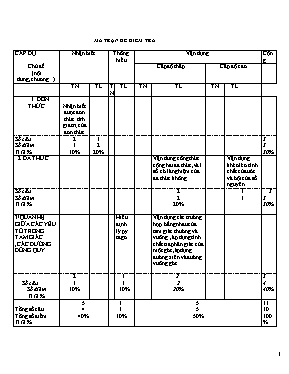
 MA TRẬN ĐỀ KIỂM TRA
CẤP ĐỘ
Chủ đề 
(nội dung,chương)
Nhận biết
Thông hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
TN
TL
TN
TL
TN
TL
TN
 TL
 1. ĐƠN THỨC
Nhận biết được đơn thức.tính gia trị của đơn thức
Số câu 
Số điểm 
Tỉ lệ %
2
1
10%
1
2
20%
3
3
30%
 2.ĐA THỨC
Vận dung công thức cộng hai đa thức,và 1 số có là nghiệm của đa thức không
Vận dụng khéo léo tính chất của ước và bội của số nguyên
Số câu 
Số điểm 
Tỉ lệ %
2
2
20%
1
1
 3
3
30% 
3/QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC ,CÁC ĐƯỜNG ĐỒNG QUY 
Hiểu định lý py tago
Vận dụng các trường hợp bằng nhau của tam giác thường và vuông ,áp dụng tính chất tia phân giác của một góc,áp dụng đường xiên và đường vuông góc
 Số câu 
Số điểm 
Tỉ lệ %
2
1
10%
1
1
10%
 2
2
20%
5`
4
40%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
5
4
40%
1
1
 10%
5
5
 50%
11
10
100%
Trường THCS TÔ Hiệu ĐỀ KIỂM TRA HỌC KỲ II 
Họ và tên ............................... Môn : Toán 7
Lớp:..................................... Thời gian :90’
Điểm 
Lời nhận xét của giáoviên
 ĐỀ BÀI
 A.Trắc nghiệm(2 điểm)
 Khoanh tròn vào đáp án mà em cho là đúng nhất:
Câu 1: Trong các biểu thức sau đâu không phải là đơn thức.
A, 4x2y B, 8-2y C, D, -2y
Câu 2. Giá trị của biểu thức tại ; là:
 A. B. C. D. .
Câu 3:Tổng ba góc trong một tam giác bằng:
 A, 1000 B,900 C, 1800 D, 3600
Câu 4: Trực tâm là giao điểm của :
 A. Ba đường phân giác. B.Ba đường cao 
 C. Ba đường trung tuyến D.Ba đường trung trực 
B.Tự luận( 8 điểm)
Câu 1: (2điểm)
a/viết 2 đơn thức đồng dạng có hai biến x và y
b/Tính tổng của 2 đơn thức vừa lấy ở trên.
c/Tính giá trị của đa thức tổng tại x=1 và y=-1.
Câu 2:(2 điểm) Cho hai đa thức:
a, Tính tổng M+N.
b, x=0 có phải là nghiệm của đa thức M+N hay không?vì sao
Câu 3: (3,0 điểm).
Cho ABC có AB = 3 cm; AC = 4 cm; BC = 5 cm.
a) Chứng tỏ tam giác ABC vuông tại A.
b)Vẽ phân giác BD (D thuộc AC), từ D vẽ DE ^ BC (E Î BC). Chứng minh DA = DE.
c) ED cắt AB tại F. Chứng minh DADF = DEDC rồi suy ra DF > DE.
Câu 4 (1,0 điểm): 
Tìm n Z sao cho ( 2n - 3 )( n + 1)
 BÀI LÀM
............................................................................................................................................................................................................................................................................................................................................................................................................................................................................
............................................................................................................................................................................................................................................................................................................................................................................................................................................................................
..................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
........................................................................................................................................................
.................................................................................................................................................................................................................................................................................................................... ..................................................................................................................................................................................................................................................................................................................................................................... ..................................................................................................................................................................................................................................................................................................................................................................................................................................................................
............................................................................................................
.................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
..............................................................................................................................
.......................................................................................................................................................... .............. ............ ............................................................................................................................................................................................................................................................................................................................................................................................................................................................................
................................................................................................................................................................................................................................................................................................................................................................................................................................................................
..................................................................................................................................................
 ĐÁP ÁN
I. TRẮC NGHIỆM ( 2 điểm):- Mỗi câu đúng được 0,5 điểm.
Câu
1
2
3
4
Đáp án
B
A
C
B
II. TỰ LUẬN: (8điểm).
Câu
Nội dung
Điểm
1
a/Lấy 2 ví dụ về đơn thức đồng dạng chứa cả hai biến x, y.
b/Tính đúng tổng của 2 đơn thức vừa lấy ví dụ ở trên.
c/Tính đúng giá trị của đa thức tổng tại x =1 và y = -1.
0,5
O,5
0,5
C2
a,Tính tổng M+N.
b, Thay x = 0 vào đa thức ta có:
 -3.03 + 02 - 0 -1= - 1
Vậy x = 0 không phải là nghiệm của đa thức 
0,5
0.5
0.5
0.5
0.5
3
Hình
vẽ
0.5
a)
Chứng minh 
Suy ra ABC vuông tại A.
0.75
b)
Chứng minh ABD = EBD (cạnh huyền – góc nhọn).
Suy ra DA = DE.
0.75
c)
Chứng minh DADF = DEDC suy ra DF = DC
Chứng minh DC > DE.
Từ đó suy ra DF > DE.
1
4
Xét các giá trị của n + 1 là ước của 5:
n + 1
-1
1
-5
5
n
-2
0
-6
4
0.5
0.5