Đề kiểm tra học kỳ 1 môn Toán Lớp 9 - Trường THCS Trà Phú

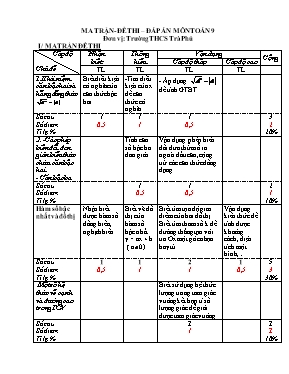
MA TRẬN- ĐỀ THI – ĐÁP ÁN MễN TOÁN 9
Đơn vị: Trường THCS Trà Phỳ
 I/ MA TRẬN ĐỀ THI
 Cấp độ
Chủ đề 
Nhận biết
Thụng hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TL
TL
TL
TL
1.Khỏi niệm căn bậc hai và hằngđẳng thức
Biết điều kiện cú nghĩa của căn thức bậc hai
-Tỡm điều kiện của x để căn thức cú nghĩa
- Áp dụng để tớnh GTBT
Số cõu 
Số điểm 
Tỉ lệ %
1
0.5
1
1
1
0,5
3
2
20%
2. -Cỏc phộp biến đổi đơn giản biểu thức chứa căn bậc hai
- Căn bậc ba
Tớnh căn số bậc ba đơn giản
Vận dụng phộp biến đổi đưa thừa số ra ngoài dấu căn, cộng trừ cỏc căn thức đồng dạng
Số cõu 
Số điểm 
Tỉ lệ %
1
0.5
1
0,5
2
1
10%
Hàm số bậc nhất và đồ thị
Nhận biết được hàm số đồng biến, nghịch biến 
Biết vẽ đồ thị của hàm số bậc nhất 
y = ax + b
 ( a0) . 
Biết tỡm tọa độ giao điểm của hai đồ thị.
Biết tỡm tham số k để đường thẳng tạo với tia Ox một gúc nhọn hay tự
Vận dụng kiến thức để tớnh được khoảng cỏch, diện tớch một hỡnh,
Số cõu 
Số điểm 
Tỉ lệ %
1
0,5
1
1
2
1
1
0,5
5
3
30%
 Một số hệ thức về cạnh và đường cao trong TGV
.
Biết sử dụng hệ thức lượng trong tam giỏc vuụng kết hợp tỉ số lượng giỏc để giải được tam giỏc vuụng 
Số cõu 
Số điểm 
Tỉ lệ %
1
1
1
1
10%
Tỷ số lượng giỏc của gúc nhọn
Dựng định nghĩa cỏc tỉ số lượng giỏc để tớnh độ dài đoạn thẳng.
Biết sử dụng TSLG của hai gúc phụ nhau
Số cõu 
Số điểm 
Tỉ lệ %
1
0,75
1
1
2
1,75
17,5%
Đường trũn
Biết vẽ hỡnh
Biết sử dụng dấu hiệu nhận biết tiếp tuyến của đường trũn
Số cõu 
Số điểm 
Tỉ lệ %
1
0,25
1
1
2
1,25
12,5%
Tổng số cõu 
Tổng số điểm
Tỉ lệ %
3
1,25
12,5%
3
2,5
25%
7
4,75
47,5%
2
1,5
15%
15
10.0
100%
II. ĐỀ KIỂM TRA:
ĐỀ KIỂM TRA THI HỌC KỲ I
 Mụn: Toỏn Lớp 9 Thời gian: 90’
I/ Lý thuyết: (2điểm)
	1) Cho A là một biểu thức, xỏc định khi nào?
 	2) Tỡm điều kiện xỏc định của căn thức : .
II/ Bài tập: (8 điểm)
Bài 1: (1,5 điểm)Tớnh a) b) 
 c) 
Bài 2: (1 điểm) Cho đường thẳng y = (5 - k)x + k - 9 (d)
 Với giỏ trị nào của k thỡ (d) tạo với trục Ox một gúc nhọn? Lỳc đú
hàm số đồng biến hay nghịch biến
Bài 3:(2 điểm) Cho hai hàm số y = -2x – 4 (d) và y = x + 4 (d’)
a) Vẽ đồ thị hai hàm số trờn cựng mặt phẳng tọa độ?
b) Gọi giao điểm của đường thẳng (d) và (d’)với trục Oy là A và B, giao điểm của hai đường thẳng là C. Xỏc định tọa độ điểm C và tớnh diện tớchABC?
Bài 4: (3 điểm) 
 Cho tam giác ABC vuông ở A cú đường cao AH. Biết AB = 6 cm; AC = 8 cm, BC = 10 cm
 a. Chứng minh: Đường thẳng AC là tiếp tuyến của đường trũn tõm B bỏn kớnh BA.
 b.Tớnh: BH; CH; AH: góc B; góc C. 
 c. Gọi AD là đường phân giác của góc A; (D thuộc BC). Tính AD ?
Bài 5 ( 1 điểm) Tớnh giỏ trị của biểu thức : 
 B= Sin210 + Sin2 20 +Sin230 +Sin240 +.........+ Sin2 88 0 + Sin2 89 0
III/ HƯỚNG DẪN CHẤM:
I/ Lý thuyết: ( 2 điểm)
Cõu
Đỏp ỏn
Điểm
1
2
 xỏc định khi A 0
 xỏc định khi 6- 2x 0
 - 2x -6 x 3
Vậy: x 3 thỡ căn thức trờn cú nghĩa
0.5
0.5
0.5
0.5
II/ Bài tập: (8 điểm)
Bài
Đỏp ỏn
Điểm
1
a) = 
b) = 4 ( vỡ 43 = 64 ) c) 
0.5
0.5
0.5
2
 Để (d) tạo với trục Ox một gúc nhọn thỡ a > 0 
 Tức là : 5 – k > 0 k < 5
 Lỳc đú hàm số đồng biến. Vỡ a= 5 – k > 0 
0.5
0.5
3
a) Xỏc định đỳng cỏc điểm thuộc đồ thị
^
 Vẽ đỳng đồ thị 2 hàm số 
b) Vỡ C là giao điểm của
 hai đường thẳng (d ) và 
 ( d’) nờn ta cú phương 
trỡnh hoành độ giao điểm:
>
 -2x - 4 = x + 4 
-3x = 8 x = 
 y = x + 4 = -+ 4 = 
Vậy C( ;)
SQMN = AB. CH = .8 .= ( đvdt)
1
0.25
0.25
0.5
4
vẽ hình đúng cho 0,25 đ
a/Ta có: BC2 = 102 = 100 
 AB2 + AC2 = 62 + 82 = 100 
 => BC2 =AB2 + AC2 = 100 
=> ABC vuụng ở A => AC BA tại A, A thuộc (B;BA). Vậy AC là tiếp tuyến của (B;BA). 
0,5 
0,5 
b) Tam giỏc ABC vuụng ở A => AB2 = BC.BH 
=> BH = AB2 : BC = 62 : 10 = 3,6 (cm) 
+ Ta cú: BC = BH + CH => 10 = 3,6 + CH 
=> CH = 10 - 3,6 = 6,4 (cm) 
+ Ta cú: AH2 = BH.CH = 3,6.6.4 = 23
 => AH = = 4,8 (cm)
+ Sin B = AC : BC = 8 : 10 = 0,8 = Sin 530 => 
 + 
0,25
0,25
0,25
0,25
c/ Tính AD:
Vì AD là phân giác 
Ta có là góc ngoài của 
Trong
Ta có :(cm) 
0,5
0,25
5
 B= Sin210 + Sin2 20 +Sin230 +....+ Sin2 88 0 + Sin2 89 0
= ( Sin210 + Sin2 890 ) + (Sin220 + Sin2 880 ) + ............
+ ( Sin2440 + Sin2 460 ) + Sin2450
= ( Sin210 + cos2 10 ) + (Sin220 + cos2 20 ) + ............
+ ( Sin2440 + cos2 440 ) + Sin2450
= 1 + 1 + .........+ 1 + = 44 + 0,5 = 44,5
0,25
0,25
0,5