Đề kiểm tra học kì II môn Toán Lớp 7 - Đề 2 - Năm học 2015-2016 - Trường THCS Chu Văn An (Có đáp án)

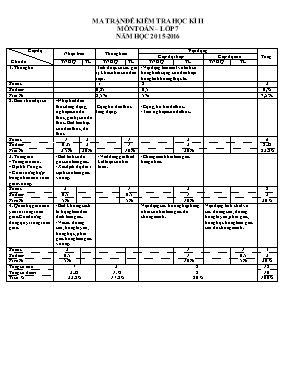
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ II
MÔN TOÁN – LỚP 7 
NĂM HỌC 2015-2016
 Cấp độ
 Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1. Thống kê
-Tính được số các giá trị khác nhau của dấu hiệu.
-Vận dụng tìm mốt và tính số trung bình cộng của dấu hiệu trong tình huống thực tế.
Số câu
 1
 2
3
Số điểm
 0,25
 0,5
0,75
Tỉ lệ %
 2,5%
 5%
7,5%
2. Biểu thức đại số
-Nhận biết đơn thức đồng dạng, nghiệm của đa thức, giá trị của đa thức. Biết tìm bậc của đơn thức, đa thức
-Cộng trừ đơn thức đồng dạng.
- Cộng, trừ hai đa thức.
- Tìm nghiệm của đa thức.
Số câu
1
2
1
2
6
Số điểm
0,25
2
1
2
5,25
Tỉ lệ %
2,5%
20%
10%
20%
52,5%
3. Tam giác 
- Tam giác cân. 
- Định lí Pitago. 
- Các trường hợp bằng nhau của tam giác vuông.
-Biết tính số đo góc của tam giác. 
-Xác định độ dài 1 cạnh của tam giác vuông. 
-Viết đúng giả thiết kết luận của bài toán.
-Chứng minh hai tam giác bằng nhau.
Số câu
2
1
2
5
Số điểm
0.5
0.5
1
2
Tỉ số %
5%
5%
10%
20%
4. Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác.
-Biết khoảng cách từ trọng tâm đến đỉnh tam giác.
-Về các đường cao, trung tuyến, trung trực, phân giác trong tam giác vuông.
Vận dụng các trường hợp bằng nhau của hai tam giác để chứng minh.
Vận dụng tính chất về các đường cao, đường trung tuyến, phân giác, trung trực trong tam giác cân để chứng minh.
Số câu
2
1
1
4
Số điểm
0.5
1
0.5
2
Tỉ số %
5%
10%
5%
20%
Tổng số câu
7
3,25
32,5%
3
1.75
17,5%
8
5
50%
18
Tổng số điểm
10
Tỉ số %
100%
ĐỀ 2:
TRƯỜNG THCS CHU VĂN AN ĐỀ KIỂM TRA HỌC KÌ II
	 Năm học: 2015 - 2016
 Môn: Toán 7 
	 Thời gian: 90 phút
 (không thể thời gian giao đề).
A. TRẮC NGHIỆM (2 điểm) 
Em hãy chọn phương án trả lời đúng nhất.
Câu 1: Điểm kiểm tra môn Toán của một nhóm học sinh được cho bởi bảng sau:
8
9
7
10
5
7
8
7
9
8
5
7
4
9
4
7
5
7
7
3
a) Số các giá trị khác nhau của dấu hiệu là:
A. 20
 B. 10
 C. 8
 D. 7
b) Mốt của dấu hiệu là:
A. 10
B. 7
C. 4
D. 3
c) Số trung bình cộng của dấu hiệu là:
A. 6,8
B. 6,6
C. 6,7
D. 6,5
Câu 2: Đơn thức nào sau đây đồng dạng với đơn thức ?
 A. 	 B. 	 C. D. 
Câu 3: Tam giác ABC có , . Số đo góc C là:
 A. 500 B. 700 C. 800 D. 900
Câu 4: Cho tam giác ABC vuông tại A, AB = 3cm và AC = 4cm thì độ dài cạnh BC là:
 A. 5 cm B. 7	 cm C. 6 cm D. 14 cm
Câu 5: Nếu AM là đường trung tuyến và G là trọng tâm của tam giác ABC thì:
 A. B. C. D. 
Câu 6: Cho tam giác ABC cân tại A, khi đó đường trung tuyến xuất phát từ đỉnh A cũng chính là:
A. Đường phân giác.
B. Đường trung trực.
C. Đường cao.
D. Đường phân giác, đường cao, đường trung trực.
B. TỰ LUẬN (8 điểm)
Bài 1: (1 điểm) Tính giá trị của biểu thức: tại x = 1 và y = 1.
Bài 2: (2 điểm) Cho hai đa thức: 	
 Tính A(x) + B(x); A(x) – B (x).
Bài 3: (2 điểm) Tìm nghiệm của các đa thức sau:
P(x) = 2x – 1
Q(x) = 
Bài 4: (3 điểm) Cho tam giác DEF cân tại D với đường trung tuyến DI.
 a) Chứng minh: DEI =DFI.
 b) Chứng minh DI ^ EF.
 c) Kẻ đường trung tuyến EN. Chứng minh rằng: IN song song với ED.
 --------------------hết---------------------
 ĐÁP ÁN VÀ THANG ĐIỂM
A. TRẮC NGHIỆM (2 điểm)
 Mỗi câu trả lời đúng được 0,25 điểm.
 Câu
1
2
3
4
5
6
a)
b)
c)
Đáp án
D
B
A
C
B
A
B
D
B. TỰ LUẬN: (8 điểm)
BÀI
ĐÁP ÁN
ĐIỂM
1
(1đ)
Thay x = 1 và y = 1 vào biểu thức 2xy + y - 1 ta được: 
2.1.1 + 1 - 1 = 2 ( 0,75đ) 
Vậy giá trị của biểu thức 2xy + y - 1 tại x = 1 và y = 1 là 2.
0,25
0,5
0,25
2
(2đ)
 A(x) = -7x4 – 2x3 + 4x2 - 2
 +
 B(x) = x4 + 4x3 - 2x2 + 3x - 5
 A(x) + B(x) = - 6x4 + 2x3 + 2x2 + 3x - 7
 A(x) = -7x4 – 2x3 + 4x2 - 2
 -
 B(x) = x4 + 4x3 - 2x2 + 3x - 5
 A(x) - B(x) = - 8x4 - 6x3 + 6x2 - 3x + 3
1
1
3
(2đ)
 a) 2x – 1 = 0 
 2x = 1 
 x = 1/2 
 Vậy x = ½ là nghiệm của đa thức 2x - 1 	
Q(x) = 2(x – 1) – 5(x + 2) +10 = 0
 2x - 2 – 5x - 10 + 10 = 0 	
 -3x = 2 	 
 x = -2/3
 Vậy x = -2/3 là nghiệm của đa thức Q(x). 
0,25
0,25
0,25
0,25
0,5
0,25
0,25
4
(3đ)
 Vẽ hình viết GT - KL đúng
D
 N
I
F
E
 DEF cân tại D
 GT IE = IF 
 ND = NF 
 KL a) Chứng minh: DEI =DFI.
 b) Chứng minh DI ^ EF.
 c) IN // ED.
 a) Xét DEI và DFI có: 
 DE = DF (vì DEF cân tại D)
 DI : cạnh chung
 IE = IF (vì DI là đường trung tuyến)
DEI =DFI ( c.c.c)
 b) Theo câu a ta có DEI =DFI ( c.c.c)
 Þ = (góc tương ứng) (1)
 mà và kề bù nên + = 1800 (2)
Từ (1) và (2) Þ = = 900 . Vậy DI ^ EF 
c) DDIF vuông (vì = 900 ) có IN là đường trung tuyến ứng với cạnh huyền DF 
Þ IN = DN = FN = DF 
Þ DDIN cân tại N Þ 
= (góc ở đáy) (1)
 *Mặt khác = (đường trung tuyến xuất phát từ đỉnh cũng là đường phân giác) (2)
 Từ (1), (2) suy ra: = nên NI // DE (hai góc so le trong bằng nhau).
0,5
0,25
0,25
0,25
0,25
0,5
0,5
0,25
0,25
Lưu ý: Học sinh làm theo cách khác đúng vẫn được điểm tối đa.
 GV ra đề 	 Tổ trưởng 	 Duyệt của BGH 
Nguyễn Thị Thu Hải