Đề kiểm tra định kì lần II - Năm 2016 - 2017 môn: Toán khối 12

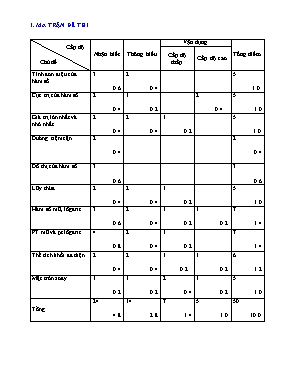
1. MA TRẬN ĐỀ THI 
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng điểm
Cấp độ thấp
Cấp độ cao
Tính đơn điệu của hàm số
3
0.6
2
0.4
5
 1.0
Cực trị của hàm số
2
0.4
1
0.2
2
 0.4
5
1.0
Giá trị lớn nhất và nhỏ nhất
2
0.4
2
0.4
1
0.2
5
 1.0
Đường tiệm cận
2
 0.4
2
0.4
Đồ thị của hàm số
3
0.6
3
0.6
Lũy thừa
2
0.4
2
0.4
1
0.2
5
1.0
Hàm số mũ, lôgarit
3
0.6
2
0.4
1
0.2
1
0.2
7
1.4
PT mũ và pt lôgarit
4
0.8
2
0.4
1
0.2
7
1.4
Thể tích khối đa diện
2
0.4
2
0.4
1
 0.2 
1
0.2
6
1.2
Mặt tròn xoay
1
0.2
1
0.2
2
0.4
1
0.2
5
1.0
Tổng
24
4.8
14
2.8
7
1.4
5
1.0
50
 10.0
Sở GD và ĐT Bắc Ninh
Trường THPT Hoàng Quốc Việt
-----------------------------------
ĐỀ KIỂM TRA ĐỊNH KÌ LẦN II- 2016- 2017
Môn: Toán- Khối 12
Thời gian: 90 phút
Cho hàm số y=. Khẳng định nào sau đây đúng?
	A. Hàm số đồng biến trên khoảng (-; 0)
	B. Hàm số nghịch biến trên khoảng (0; + )
	C. Hàm số đồng biến trên khoảng (0; 1)
	D. Hàm số nghịch biến trên khoảng (-; -1) và (0; +)
Cho hàm số y=. Khẳng định nào sau đây đúng?
 	A. Hàm số đạt cực tiểu tại x=-1
 	B. Hàm số đạt cực tiểu tại x=3
 	C. Hàm số có giá trị lớn nhất tại x=-1
 	D. Hàm số đạt giá trị nhỏ nhất tại x=3
Trong các hàm số sau, hàm số nào sau đây đồng biến trên khoảng (1; 3)? 
	A. 	B. 	C. 	D. 
 Cho hàm số: . Khẳng định nào sau đây sai?
 	A. Hàm số nghịch biến trên R	
 	B. Hàm số nghịch biến trên (-; 2) và (2; +)
 	C. Đồ thị hàm số có tiệm cận đứng x=2
 	D. Đồ thị hàm số có tiệm cận ngang y=1
Hàm số đồng biến trên khoảng (2; +) với giá trị của m là:
	A. m	D. m>
Số cực trị của hàm số y= là:
 	A. 4	B. 2	C. 3	D. 1
 Hàm số f(x) = đạt cực trị tại điểm:
	A. x = e	B. x = 	C. x = 2	D. x = 3
Hàm số đạt cực tiểu tại x = 2 khi :
	A. 	B. 	C. 	D. 
 Cho hàm số y=x3-3mx+2 (Cm). Tìm m để đường thẳng đi qua 2 điểm cực đại, cực tiểu của đồ thị hàm số cắt đường tròn tâm I(1; 1), bán kính R=1 tại A, B sao cho diện tích tam giác IAB lớn nhất
 	A m=	B. m= 	C. m=3	D. Đáp án khác
 Cho hàm số:. Tìm m để đồ thị hàm số có 3 điểm cực trị lập thành tam giác có 1 góc bằng 1200.
	A. m=	B. m=	C. m=	D. m= 
 Cho hàm số: . Khẳng định nào sau đây đúng?
Đồ thị có tiệm cận đứng y=2
Đồ thị có tiệm cận ngang y=2
C. Đồ thị có tiệm cận đứng x=2; tiệm cận ngang y=1
Đồ thị có tiệm cận đứng x=-2
 Cho hàm số: . Đồ thị hàm số có tất cả số tiệm cận là:
	 A. 1	B. 2	C. 3	D. 4
13. Đồ thị sau đây là của hàm số nào trong các hàm số sau?
 y 
	 x 
	A. 	B. 	
	C. 	D.
14. Đồ thị sau đây là của hàm số nào ? Chọn 1 câu đúng.
A. 	B.	C.	D.
	y
x
Cho f(x) là hàm số xác định và liên tục trên R có bảng biến thiên sau. Tìm m để đồ thị hàm số y=f(x) cắt đường thẳng (d) : y=m tại 3 điểm phân biệt.
 A. 3< m<5
 B. m=5; m=3
 C. 
 D. m<3
Giá trị lớn nhất của hàm số trên tập xác định D là:
 	A. 	B. 	C. 	D. 
 Giá trị lớn nhất của hàm số trên là:
 A. ymax=	B. ymax =0	C. ymax = 2	D. ymax = 
 Hàm số đạt giá trị nhỏ nhất trên đoạn [-4 ; 4] tại giá trị của x là:
 	A. -41	B. -1	C. -4	D. 40
 Nghiệm của phương trình là:
A.Vô nghiệm	B. -3 và 27	C. 27	D. và 27
20. Giá trị nhỏ nhất của hàm số trên [2 ; 3] là:
A. e	B. 1	C. 4-2ln2	D. -2 + 2ln2
21. Cho . Mệnh đề nào sau đây là đúng?
	A. a5> 	B. a2 -
22. Tập xác định của hàm số là :
A. 	B. 	C. 	D. 
23. Tìm m để phương trình có 2 nghiệm x1, x2 sao cho:
	 x1.x2 = 125.
A. m = 	B. m = 25	C. m = 2	D. m = 
24. Biểu thức A= rút gọn là:
	A. 	B. 	C. 	D. 
25. Hàm số y = có tập xác định là:
A. (1; + ¥)	B. (- ¥; +¥ )	 C. (-; 1]	 D. (- ¥; 1)
26. Một người gửi tiết kiệm triệu đồng vào một ngân hàng với lãi suất một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Sau năm mới rút lãi thì người đó được số tiền lãi là:
	A. triệu đồng	 	B. triệu đồng 
	C. triệu đồng 	D.triệu đồng
27. Nếu (a, b > 0) thì x bằng:
A. 	B. 	C. 	D. 
 28. Đạo hàm của hàm số là
A. 	B. 	C. 	D.
29. Hàm số y = có đạo hàm là:
	A. y’ = x2ex	B. y’ = -2xex	C. y’ = (2x - 2)ex	D. KÕt qu¶ kh¸c
30. Biết . Khi đó giá trị của bằng
A. 	B. 	C. 	D. 
31. Cho log153=a, log103=b. Biểu diễn log50 theo a, b
	A. 	B.	C. 	D. 
32. Tìm m để phương trình có 2 nghiệm x.
A. -2 m 2.	B. – 2< m <2.	C. -2 m 0.	D. -2 < m< 0.
33. Phương trình: có nghiệm là : 
	A. x=-3	B. x=2	C. x=3	D. x=5
34. Phương trình có nghiệm là:
A. x=1	B. x=-1	C. x=0	D. Cả 3 đều sai
35. Phương trình: (2x-3)x=1 có nghiệm là :
	A. x=0 ; x=2	B. Vô	nghiệm	C. x=1	D. Đáp án khác
36. Phương trình: 9x +6x=2.4x có nghiệm là :
	A. x= 3	B. x= 2	C. x= 1	D. x=0
37. Phương trình log(x2-1)=2 có nghiệm là:
	A. x=2 ; x=-2	B. x=1+2	C. x=	D. x=2
38. Phương trình ln(x-1)-ln(4x5+7)=0 có nghiệm :
	A. x=-3	B. x=3	C. Vô nghiệm	D. Nghiệm đúng với mọi x 
39. Phương trình: log2x+ log4x+ log8x=11 có nghiệm là:
	A. 24	B. 36	C. 45	D. 64
40. Cho chóp tứ giác đều S.ABCD có AB=a ; đường cao h=3a. Thể tích khối chóp S.ABCD bằng :
	A. a3	B. 3a3 	C. 	D. Đáp án khác
41. Cho hình hộp chữ nhật có . Thể tích khối hộp chữ nhật là :
	A. 	B. 	C. 	D. 
42. Cho hình chóp có đáy là hình thoi với , 
	, . Thể tích khối chóp là: 
A. 	B. 	C. 	D. 
43. Cho hình lăng trụ đứng tam giác , tam giác có, góc , . Thể tích khối lăng trụ là: 
A. 	B. 	C. 	D. 
44. Cho chóp S. ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu của S lên mặt phẳng đáy là trung điểm H của AB. Mặt phẳng (SAD) tạo với mặt đáy góc 600. Tính khoảng cách từ B đến mặt phẳng (SCD).
	A. 	B. 	C. 	D. a
45. Cho chóp S. BCD có đáy ABCD là hình bình hành. M là trung điểm SC, mặt phẳng (ABM) cắt SD tại N. Tỉ số thể tích bằng:
	A. 	B. 	C. 	D. 
46. Cho hình bình hành ABCD có góc ABC bằng 1200, AD=2cm và tam giác ABD vuông tại D. Cho hình bình hành ABCD quay xung quanh cạnh BC ta được khối tròn xoay có thể tích bằng:
	A. V=	B. V=	C. V=12	D. V=24
47. Tam giác ABC vuông tại A, có AB=10; AC=15. Cho tam giác ABC quanh xung quanh cạnh BC ta được 2 hình nón có diện tích xung quanh tương ứng là S1, S2. Tỉ số. Hệ thức nào dưới đây đúng?
	A. S1= S2	B. 3S1=2 S2	C.2 S1= 3S2	D. 5S1=2S2
48. Hình chữ nhật ABCD có AB=10; AD=15. cho hình chữ nhật ABCD quay xung quanh AB và AD ta được 2 khối trụ tròn xoay có thể tích tương ứng là V1, V2. Tính tỉ số .
	A. 	B. 	C. 1	D. Cả 3 đều sai
49. Cho hình nón có độ dài đường sinh l=5; bán kính r=3. Diện tích xung quanh của hình nón đó là:
A. 30	B. 15	C. 20	D. 75
50. Từ một chiếc thùng tôn hình trụ đã hỏng đáy, sau khi đã bỏ đáy đi và cắt chiếc thùng ấy theo một đường thẳng vuông góc với 2 đáy của thùng người ta được một miếng tôn hình chữ nhật như hình 
vẽ. Biết rằng miếng tôn hình chữ nhật đó có kích thước 2 cạnh là 30cm, 80cm. Tính thể tích của chiếc thùng ban đầu.
	A. V=	B. V=	
	C. V=	D. V=