Đề kiểm tra chương 1 Hình học 9

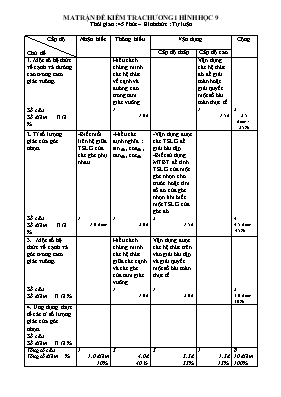
MA TRẬN ĐỀ KIỂM TRA CHƯƠNG 1 HÌNH HỌC 9 
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
1. Một số hệ thức về cạnh và đường cao trong tam giác vuông.
Hiểu cách chứng minh các hệ thức về cạnh và đường cao trong tam giác vuông
Vận dụng các hệ thức đó để giải toán hoặc giải quyết một số bài toán thực tế.
Số câu 
Số điểm Tỉ lệ %
1
1,0đ 
1
1,5đ 
2
2,5 điểm= 25% 
2. Tỉ số lượng giác của góc nhọn.
-Biết mối liên hệ giữa TSLG của các góc phụ nhau.
-Hiểu các định nghĩa : sin, cos, tan, cot.
-Vận dụng được các TSLG để giải bài tập.
-Biết sử dụng MTBT để tính TSLG của một góc nhọn cho trước hoặc tìm số đo của góc nhọn khi biết một TSLG của góc đó.
Số câu 
Số điểm Tỉ lệ %
1
1,0 điểm
1
2,0đ 
2
1,5đ 
4
4,5 điểm
 45% 
3. Một số hệ thức về cạnh và góc trong tam giác vuông.
Hiểu cách chứng minh các hệ thức giữa các cạnh và các góc của tam giác vuông.
Vận dụng được các hệ thức trên vào giải bài tập và giải quyết một số bài toán thực tế
Số câu 
Số điểm Tỉ lệ %
1
1,0đ 
1
2,0đ 
2
3,0 điểm 30% 
4. Ứng dụng thực tế các tỉ số lượng giác của góc nhọn.
Số câu 
Số điểm Tỉ lệ %
Tổng số câu 
Tổng số điểm %
1
1,0 điểm
10%
3
4,0đ 
40 % 
3
3,5đ
35% 
1
1,5đ
15%
8
10 điểm
100%
Thời gian : 45 Phút – Hình thức : Tự luận
Họ và tên .. KIỂM TRA HÌNH HỌC CHƯƠNG I
Lớp: Thời gian: 45’
Điểm
Lời phê của GV
Bài 1: (2,5điểm) Cho tam giác ABC vuông tại A có AB = 5cm, AC = 12cm, BC = 13cm.
Tính tỉ số lượng giác của góc nhọn B 
Tính số đo của góc B( làm tròn đến độ) 
 Bài 2: (1điểm) Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn : ; ; ; 
Bài 3 (1điểm): Tính giá trị biểu thức (không dùng máy tính)
 A = sin2 750 + sin2 150 - cos2 500 - cos2 400 + cot 400. cot 500
Bài 4 (3,5điểm): Cho tam giác vuông ABC, kẻ đường cao AH. Từ H kẻ HE vuông góc AB (E thuộc AB), kẻ HF vuông góc AC (F thuộc AC)
	a) Chứng minh rằng : AE . AB = AF . AC
	b) Cho AB = 5cm ; AH = 4cm. Tính AE
	c) Cho = 300. Tính HF
Bài 5 (2đ): Một cây bàng có bóng trên mặt đất đo được là 3,6 m, các tia sáng của mặt trời tạo với mặt đất một góc bằng 520. Tính chiều cao của cây bàng .
( Làm tròn đến chữ số thập phân thứ nhất).
ĐÁP ÁN
Bài 1: (2,5điểm) 
a). sinB = (0,5đ) cosB = (0,5đ)
 tanB = (0,5đ) cotB = (0,5đ)
b).sinB (0,5đ)
Bài 2: (1điểm) 
= (0,25đ)
(0,25đ)
(0,25đ)
(0,25đ)
Bài 3 (1điểm): A = sin2 750 + sin2 150 - cos2 500 - cos2 400 + cot 400. cot 500
 = (sin2 750 + sin2 150) – (cos2 500 + cos2 400) + tan 500. cot 500 (0,5đ)
 = 1 – 1 + 1 = 1 (0,5đ)
Bài 4 (3,5điểm): 
Hình vẽ: 0,25đ
a). (1,5đ) Chứng minh rằng : AE . AB = AF . AC 
 * AHB vuông tại H mà HEAB tại E 
 nên: AH2 = AE.AB (1) (0,5đ) 
 * AHC vuông tại H mà HFAC tại F 
 nên AH2 = AF.AC (2) (0,5đ)
 Từ (1) và (2) ta suy ra: AE.AB = AF.AC. (0,25đ)
b). (1đ) Tính AE
 Từ hệ thức AH2 = AE.AB (0,5đ)
Suy ra : AE = = =(cm) (0,5đ)
c). Tính HF
Xét HAF, có: HF = AH .sin 
HF = 4 .sin 300 = 2(cm)
Bài 5 (2đ): 
AB = AC.tanC (1đ)
 = 3,6.tan520 4,6 (0,75đ)
Vậy chiều cao cây bàng là 4,6 m (0,25đ)