Đề kiểm tra chương 1 Hình 9 có ma trận

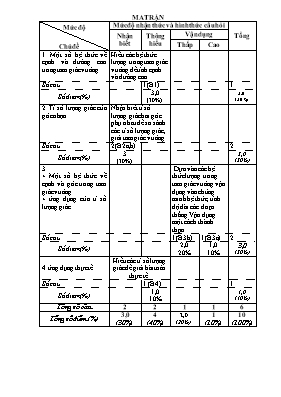
MA TRẬN
Mức độ
Chủ đề
Mức độ nhận thức và hình thức câu hỏi
Tổng
Nhận biết
Thông hiểu
Vận dụng
Thấp
Cao
1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
Hiểu các hệ thức lượng trong tam giác vuông để tính cạnh và đường cao.
Số câu
1(B1)
1
Số điểm (%)
3,0
(30%)
3,0
(30%)
2. Tỉ số lượng giác của góc nhọn
Nhận biết tỉ số lượng giác hai góc phụ nhau để so sánh các tỉ số lượng giác, giải tam giác vuông
Số câu
2(B2a,b)
2
Số điểm (%)
3
(30%)
3,0
(30%)
3. 
+ Một số hệ thức về cạnh và góc trong tam giác vuông
+ ứng dụng của tỉ số lượng giác
 Dựa vào các hệ thức lượng trong tam giác vuông vận dụng vào chứng minh hệ thức, tính độ dài các đoạn thẳng.	Vận dụng một cách thành thạo.
Số câu
1(B3b)
1(B3a)
2
Số điểm (%)
2,0
20%
1,0
10%
3,0
(30%)
4. ứng dụng thực tế
Hiểu các tỉ số lượng giác để giải bài toán thực tế.
Số câu
1 (B4)
1
Số điểm (%)
1,0
10%
1,0
(10%)
Tổng số câu
2
2
1
1
6
Tổng số điểm (%)
3,0
(30%)
4
(40%)
2,0
(20%)
1
(10%)
10
(100%)
ĐỀ BÀI
Bài 1 : (3,0 điểm)
	Cho tam giác ABC vuông tại A, kẻ đường cao AH, biết BH = 4, CH = 9. 
Tính độ dài các đoạn AB, AC, AH.
Bài 2 : (3,0 điểm)
	a) Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần
	sin240 , cos350 , sin540 , cos700 , sin780 
	b) Giải tam giác ABC vuông tại A biết BC = 10cm ; = 600
Bài 3 : (3,0 điểm)
	Cho tam giác nhọn ABC, kẻ đường cao AH. Từ H kẻ HE vuông góc AB (E thuộc AB), kẻ HF vuông góc AC (F thuộc AC)
	a) Chứng minh rằng : AE . AB = AF . AC
	b) Cho BH = 3cm; AH = 4cm. Tính AE, BE
Bài 4 : (1,0 điểm)
	Một cột cờ cao 7m có bóng trên mặt đất dài 4m. Tính góc a mà tia sáng mặt trời tạo với mặt đất (làm tròn đến phút)
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM
Bài
Câu
Nội dung chấm
Điểm chi tiết
Tổng số điểm
1
+ Hình vẽ 
9
4
+ BC = BH + CH = 4 + 9 = 13
+ AB2 = BH.BC = 4.13 = 52 AB = 
+ AC2 = CH.BC = 9.13 = 117 AC = 
+ AH2 = BH.CH = 4.9 = 36 AH = 6
0,5
1,0
1,0
0,5
3,0
2
a
+ cos350 = sin550 
+ cos700 = sin200 
+ Vì 200 < 240 < 540 < 550 < 780 
+ Nên : sin200 < sin240 < sin540 < sin550 < sin780 
+ Vậy : cos700 < sin240 < sin540 < cos350 < sin780 
0,25
0,25
0,25
0,25
0,50
3,0
b
+ + = 900 suy ra : = 900 – 600 = 300 
+ AB = BC.sin300 suy ra : AB = 5cm
+ AC = BC.sin600 suy ra : AC = 5
0,50
0.50
0.50
3
a
+ Hình vẽ
áp dụng hệ thức lượng cho DAHB và DAHC
+ AH2 = AE.AB
+ AH2 = AF.AC
+ Suy ra : AE.AB = AF.AC
0,25
0,25
0,25
0,25
3,0
b
+ Tính đúng AB = 5cm 
từ hệ thức AH2 = AE.AB 
Suy ra : AE = = =3,2
+ BE = AB – AE = 5 – 3,2 = 1,8
0,50
0,25
0,75
0,50
4
+ Tính đúng : 
+ Suy ra : a » 60015’
0,50
0,50
1,0