Đề kiểm tra 45 phút - Chương I: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Trường THPT Phan Bội Châu
 Tổ Toán 
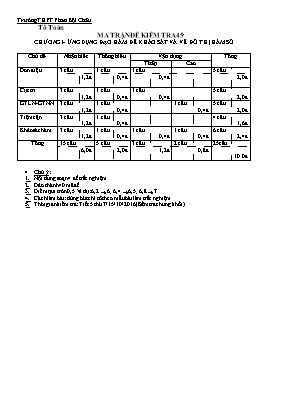
MA TRẬN ĐỀ KIỂM TRA 45/
CHƯƠNG I- ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Thấp
Cao
Đơn điệu
3 câu
1 câu
1 câu
5 câu
1,2đ
0,4đ
0,4đ
2,0đ
Cực tri
3 câu
1,2đ
1 câu
0,4đ
1 câu
0,4đ
5 câu
2,0đ
GTLN-GTNN
3 câu
1,2đ
1 câu
0,4đ
1 câu
0,4đ
5 câu
2,0đ
Tiệm cận
3 câu
1,2đ
1 câu
0,4đ
4 câu
1,6đ
Khảo sát hàm
3 câu
1,2đ
1 câu
0,4đ
1 câu
0,4đ
1 câu
0,4đ
6 câu
2,4đ
Tổng
15 câu
5 câu
3 câu
2 câu 
25câu 
6,0đ
2,0đ
1,2đ
0,8đ
10.0đ
Chú ý:
Nội dung soạn 4 đề trắc nghiệm.
Đảo thành 40 mã đề.
Điểm qui tròn 0,5.Ví dụ: 6,2 6; 6,4 6,5; 6,8 7.
Cách làm bài: dùng bút chì tô theo mẫu bài làm trắc nghiệm.
Thời gian kiểm tra: Tiết 5 thứ 7/15/10/2016(Kiểm tra chung khối).
Họ và tên :
Đề 2
Lớp :
Câu 1. Hỏi hàm số y = nghịch biến trên khoảng nào?
A. (-1;3) 	B. ( -; -1) và ( 3; +) 	C. ( 3; +) 	D. (-;3)
Câu 2. Hỏi hàm số y = nghịch biến trên khoảng nào?
A. R 	B. ( -;1) và (1;+ ) 	C. R \ {1} 	D. ( -;-1) và (-1;+ )
Câu 3. Hỏi hàm số đồng biến trên khoảng nào?
A.	B. 	C. 	D. 
Câu 4. Hỏi hàm số đồng biến trên khoảng nào?
A. 	B. (0 ; 1) 	C. (1 ; 2 ) 	D. 
Câu 5. Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên R.
A. ( -1; 0) 	B. ( - ; -1) (0; +) 	C. [-1; 0] 	D. ( - ; -1] [ 0; +) 
Câu 6. Tìm điểm cực đại của hàm số y = .
A. x = 0 	B. x = 2 	C. (0; 2) 	D. ( 2; 6)
Câu 7. Tìm điểm cực tiểu của đồ thị hàm số .
A.	B. 	C. 	D. 
Câu 8. Tìm điểm cực đại của hàm số .
A. 	B. 	C. 	D.
Câu 9. Cho hàm số có hai điểm cực trị là . Hỏi tích là bao nhiêu ?
A. – 8	B. 8	C. 5	D. - 5
Câu 10. Tìm tất cả các giá trị thực của tham số m để hàm số y = x3 – 2mx + 1 đạt cực tiểu tại x = 1 ?
A. m = -	B. m = - 	C. m = 	D. m = 
Câu 11. Hàm số có giá trị lớn nhất và giá trị nhỏ nhất của trên đoạn lần lượt là M và m. Tìm M và m.
A. 	B. 	C. 	D. 
Câu 12. Tìm giá trị lớn nhất của hàm số trên đoạn 
A. 	B. 	C. 	D. 
Câu 13. Giá trị lớn nhất, nhỏ nhất của hàm số: lần lượt là:
A. 4; -4 B. 4; 4 C. 4; -4 D. 4; 2
Câu 14. Tìm tất cả các giá trị thực của tham số m để hàm số của hàm số trên có giá trị lớn nhất trên đoạn [2; 3] là .
A. 0 	B. 1 	C. -5 	D. – 2
Câu 15. Tiệm cận đứng của đồ thị hàm số là
A. 	B. 	C. 	D. 
Câu 16. Tìm phương trình đường tiệm ngang và tiệm cận đứng của đồ thị hàm số  là:
A. y= 1 và x = 3 	B. y = x+2 và x = 1 	C. y = 3 và x = 1 	D. y = -3 và x = 1
Câu 17. Tìm phương trình đường tiệm ngang và tiệm cận đứng của đồ thị hàm số . 
A. 	B. 	C. 	D. 
Câu 18. Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận ?
A. 2	B. 1	C. 4	D. 3
Câu 19. Bảng biến thiên trong hình bên dưới là bảng biến thiến của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? 
A. 	B. 	C. 	D. 
Câu 20. Đồ thị trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A. 	B. 	C. 	D. 
Câu 21. Đồ thị trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A. B. C. D. 
Câu 22. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số tại 3 điểm phân biệt.
A. 	B. 	C. 	D. 
Câu 23. Tìm các giá trị thực của tham số m để đường thẳng cắt đồ thị hàm số tại 2 điểm phân biệt A, B sao cho .
A. 	B. 	C. 	D. 
Câu 24. Tìm các giá trị thực của tham số m để phương trình có 3 nghiệm phân biệt.
A. 	B. 	C. 	D. .
Câu 24. Tìm m để hàm số đồng biến trên khoảng .
A. 	B. 	C. 	D.