Đề kiểm tra 1 tiết môn: Hình học 9 ( tiết 16 tuần 08 theo ppct)

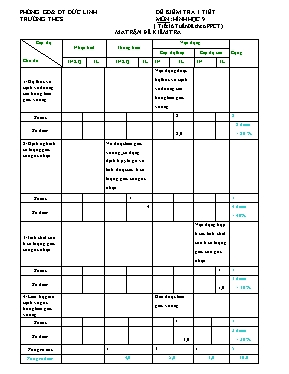
PHÒNG GD& ĐT ĐỨC LINH	ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THCS 	MÔN: HÌNH HỌC 9
 ( Tiết 16 Tuần 08 theo PPCT)
MA TRẬN ĐỀ KIỂM TRA 
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TN
TL
TN
TL
1/ Hệ thức về cạnh và đường cao trong tam giác vuông
Vận dụngđược hệ thức về cạnh và đường cao trong tam giác vuông
Số câu
2
2
Số điểm
 2,0
2 điểm
 = 20 %
2/ Định nghiã tỉ số lượng giác của góc nhọn
Vẽ được tam giác vuông,, sử dụng định lí py ta go và tính được các tỉ số lượng giác của góc nhọn
Số câu
1
1
Số điểm
4
4 điểm
= 40%
3/Tính chất của tỉ số lượng giác của góc nhọn
Vận dụng hợp lí các tính chất của tỉ số lượng giác của góc nhọn
Số câu
1
1
Số điểm
1,0
1 điểm
= 10 %
4/ Liên hệ giữa cạnh và góc trong tam giác vuông
Giải được tam giác vuông
Số câu
1
1
Số điểm
3,0
3 điểm
 = 30%
Tổng số câu
1
3
1
5
Tổng số điểm
4,0
5,0
1,0
10.0
PHÒNG GD & ĐT ĐỨC LINH	KIỂM TRA 1 TIẾT
TRƯỜNG THCS .	MÔN : HÌNH HỌC 9
 ĐỀ SỐ : 1 	 (Tiết 16 Tuần 8 Theo PPCT)
Họ và tên : 
Lớp : 9 .......
Điểm 
Lời phê của Thầy 
ĐỀ: 
Bài 1: (4 điểm). Cho tam giác ABC . Biết AB = 5cm, AC = 12cm, BC = 13cm.
 Tính các tỉ số lượng giác của góc B
Bài 2: (6 điểm).
Cho ABC vuông tại A Biết AB = 3cm, BC = 5cm. 	
1/ Giải tam giác vuông ABC.( số đo góc làm tròn đến độ)
2/ Từ B kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AC tại D . Tính độ dài các đoạn thẳng AD, BD
	3/ Gọi E,F lần lượt là hình chiếu của A trên BC và BD . Chứng minh : BF.BD = BE.BC
4/ Tính: Sin4B – cos4B + 2cos2B
BÀI LÀM
PHÒNG GD&ĐT ĐỨC LINH	HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THCS .	MÔN: HÌNH HỌC 9
 ĐỀ SỐ 1 ( Tiết 16 Tuần 8 theo PPCT)
Bài 
Nội dung
Điểm
1
(4 điểm)
ABC có : BC2 = 132 = 169, AB2 + AC2 = 52 + 122 = 169
Do đó: BC2 = AB2 + AC2 
Suy ra: ABC vuông tại A(định lí Py-ta-go đảo)
Theo định nghĩa tỉ số lượng giác trong tam giác vuông, ta có:
;
(1 điểm)
(0,5 điểm)
(0,5 điểm)
(Mỗi tỉ số đúng 0,5 điểm)
2
(5,5 điểm)
 1/ Giải tam giác vuông ABC.
ABC vuông tại A, theo định lý Py-ta-go ta có : 
BC2 = AB2 + AC2 
Ta lại có: 
Nên : 
2/ Tính độ dài các đoạn thẳng AD, BD
BCD vuông tại B, đường cao BA theo hệ thức về cạnh và đường cao trong tam giác vuông ta có :
AB2 = ADAC 
BD2 = ADDC = AD(AD+AC) = 2,25.6,25= 14,0625
BD= = 3,75 cm
3/ Chứng minh : BF.BD = BE.BC
BAD vuông tại A, đường cao AF
Nên AB2 = BF.BD (hệ thức cạnh và đường cao)
ABC vuông tại A, đường cao AE
Nên AB2 = BE.BC (hệ thức cạnh và đường cao)
Vậy BF.BD = BE.BC
4/ Sin4B – cos4B + 2cos2B
Vẽ hình đúng đến câu a cho 0,5 điểm)
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
Chú ý: Học sinh giải theo cách khác đúng vẫn cho điểm tối đa.
PHÒNG GD & ĐT ĐỨC LINH	KIỂM TRA 1 TIẾT
TRƯỜNG THCS ..	MÔN : HÌNH HỌC 9
 ĐỀ SỐ : 2 	 (Tiết 16 Tuần 8 Theo PPCT)
Họ và tên : 
Lớp : 9 .......
Điểm 
Lời phê của Thầy 
ĐỀ: 
Bài 1: (4 điểm). Cho tam giác ABC vuông tại A. Biết AB = 6cm, AC = 4,5 cm.
 Tính các tỉ số lượng giác của góc B
Bài 2: (6 điểm).
Cho ABC vuông tại A Biết AC = 3cm, BC = 5cm. 	
1/ Giải tam giác vuông ABC. ( số đo góc làm tròn đến độ)
2/ Từ C kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AB tại D . Tính độ dài các đoạn thẳng AD, CD
	3/ Gọi E,F lần lượt là hình chiếu của A trên BC và CD . Chứng minh : CF.CD = CE.BC
4/ Tính: cos6B + sin6B + 3sin2cos2B
BÀI LÀM
PHÒNG GD&ĐT ĐỨC LINH	HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THCS .	MÔN: HÌNH HỌC 9
 ĐỀ SỐ 2 ( Tiết 16 Tuần 8 theo PPCT)
Bài 
Nội dung
Điểm
1
(4 điểm)
ABC vuông tại A theo định lí Py-ta-go ta có :
 BC2 = AB2 + AC2 
Suy ra: 
Theo định nghĩa tỉ số lượng giác trong tam giác vuông, ta có:
;
(1 điểm)
(0,5 điểm)
(0,5 điểm)
(Mỗi tỉ số đúng 0,5 điểm)
2
(5,5 điểm)
 1/ Giải tam giác vuông ABC.
ABC vuông tại A, theo định lý Py-ta-go ta có : 
BC2 = AB2 + AC2 
Ta lại có: 
Nên : 
2/ Tính độ dài các đoạn thẳng AD, CD
BCD vuông tại C, đường cao CA theo hệ thức về cạnh và đường cao trong tam giác vuông ta có :
AC2 = ABAD 
CD2 = ADDB = AD(AD+AB) = 2,25.6,25= 14,0625
BD= = 3,75 cm
3/ Chứng minh : CF.CD = CE.BC
ADC vuông tại A, đường cao AF
Nên AC2 = CF.CD (hệ thức cạnh và đường cao)
ABC vuông tại A, đường cao AE
Nên AC2 = CE.BC (hệ thức cạnh và đường cao)
Vậy BF.BD = BE.BC
4/ cos6B + sin6B + 3sin2cos2B
Vẽ hình đúng đến câu a cho 0,5 điểm)
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
Chú ý: Học sinh giải theo cách khác đúng vẫn cho điểm tối đa.