Đề kiểm tra 1 tiết môn Hình học 10

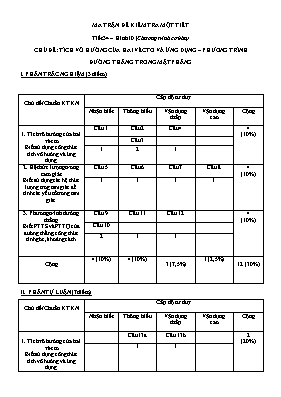
MA TRẬN ĐỀ KIỂM TRA MỘT TIẾT
Tiết 34 – Hình 10 (Chương trình cơ bản)
CHỦ ĐỀ: TÍCH VÔ HƯỚNG CỦA HAI VÉCTƠ VÀ ỨNG DỤNG – PHƯƠNG TRÌNH
ĐƯỜNG THẲNG TRONG MẶT PHẲNG
I. PHẦN TRẮC NGHIỆM (3 điểm)
Chủ đề/Chuẩn KTKN
Cấp độ tư duy
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Cộng
1. Tích vô hướng của hai véctơ
Biết sử dụng công thức tích vô hướng và ứng dụng
Câu 1
Câu 2
Câu 4
4
(10%)
Câu 3
1
2
1
2. Hệ thức lượng trong tam giác
Biết sử dụng các hệ thức lượng trog tam giác để tính các yếu tố trong tam giác
Câu 5
Câu 6
Câu 7
Câu 8
4
(10%)
1
1
1
1
3. Phương trình đường thẳng
Biết PTTS và PTTQ của đường thẳng, công thức tính góc, khoảng cách
Câu 9
Câu 11
Câu 12
4
(10%)
Câu 10
2
1
1
Cộng
4 (10%)
4 (10%)
3 (7,5%)
1 (2,5%)
12 (30%)
II. PHẦN TỰ LUẬN (7điểm)
Chủ đề/Chuẩn KTKN
Cấp độ tư duy
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Cộng
1. Tích vô hướng của hai véctơ
Biết sử dụng công thức tích vô hướng và ứng dụng
Câu 13a
Câu 13b
2
(20%)
1
1
2. Hệ thức lượng trong tam giác
Biết sử dụng các hệ thức lượng trog tam giác để tính các yếu tố trong tam giác
Câu 14a
Câu 14b
2
(20%)
1
1
3. Phương trình đường thẳng
Biết PTTS và PTTQ của đường thẳng, công thức tính góc, khoảng cách
Câu 15a
Câu 15b
Câu 15c
3
(30%)
1
1
1
Cộng
1 (10%)
3 (30%)
2 (20%)
1 (10%)
7
(70%)
BẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎI ĐỀ KIỂM TRA
Tiết 34 – Hình 10 (Chương trình cơ bản)
CHỦ ĐỀ: TÍCH VÔ HƯỚNG CỦA HAI VÉCTƠ VÀ ỨNG DỤNG – PHƯƠNG TRÌNH
ĐƯỜNG THẲNG TRONG MẶT PHẲNG
I. PHẦN TRẮC NGHIỆM (3 điểm)
CHỦ ĐỀ
CÂU
MÔ TẢ
1. Tích vô hướng của hai véctơ
1
Nhận biết GTLG của góc đặc biệt
2
Thông hiểu tính tích vô hướng bằng định nghĩa
3
Thông hiểu tính góc giữa hai véctơ biết tọa độ của hai véctơ
4
Vận dụng tính tọa độ điểm thỏa mãn đẳng thức vectơ
2. Hệ thức lượng trong tam giác
5
Nhận biết: diện tích tam giác biết độ dài hai cạnh và góc xen giữa
6
Thông hiểu tính bán kính đường tròn ngoại tiếp tam giác bằng cách áp dụng định lý sin
7
Vận dụng tính bán kính đường tròn nội tiếp tam giác 
8
Vận dụng cao: bài toán thực tế về đo đạc
3. Phương trình đường thẳng
9
Nhận biết véctơ pháp tuyến của đường thẳng
10
Nhận biết phương trình tham số của đường thẳng
11
Thông hiểu tính khoảng cách từ một điểm đến một đường thẳng
12
Thông hiểu tính góc gữa hai đường thẳng 
II. PHẦN TỰ LUẬN (7điểm)
CHỦ ĐỀ
CÂU
MÔ TẢ
41. Tích vô hướng của hai véctơ
13a
Thông hiểu tính tích vô hướng của hai vectơ
13b
Vận dụng tính tọa độ trực tâm tam giác
2. Hệ thức lượng trong tam giác
14a
Thông hiểu tính cạnh hoặc góc trong tam giác 
14b
Vận dụng cao chứng minh hệ thức lượng giác
3. Phương trình đường thẳng
15a
Nhận biết viết phương trình đường thẳng
15b
Thông hiểu viết phương trình đường thẳng
15c
Vận dụng tìm tọa độ điểm thuộc đường thẳng 
Họ và tên:
Lớp:
ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 10-01
Thời gian làm bài: 45 phút
I. PHẦN TRẮC NGHIỆM (3 điểm)
Câu 1: Trong các đẳng thức sau ,đẳng thức nào đúng:
A. sin1200 = 	B. cot1200 = 	C. cos1200 = D. tan1200 = 
Câu 2: Cho tam giác ABC đều cạnh a, AH là đường cao của tam giác ABC. Khi đó :
A. 	B. 	C. 	D. 
Câu 3: Cho 2 véc tơ và . Tích vô hướng .là:
A.-16	B.37	C.40	D. 12
Câu 4: Cho ba điểm .Tọa độ điểm E thỏa mãn: là:
 A.E(2;12) B.E(-2;-12) C.E(--2;12) D.E(2;-12)
Câu 5: Cho tam giác ABC có b=7cm,a=10cm và . Diện tích S của tam giác ABC là:
 	 B. 
Câu 6: Cho tam giác có . Bán kính đường tròn ngoại tiếp tam giác là :
 A.5 B. 10 C. D
Câu 7: Cho tam giác ABC có ba cạnh là 6,8,10. Bán kính đường tròn nội tiếp tam giác ABC là : 
 A. B.4 C.2 D.1
Câu8: Cho tam giác ABC với AC=10m, . Cạnh AB gần kết quả nào nhất bằng:
 A .8,7 m B. 8,5 m C.11m D.9,0m
Câu 9: Cho đường thẳng d có phương trình tổng quát . :Vectơ pháp tuyến của d là:
 A. B. C. D. 
Câu 10: Cho đường thẳng qua A(0;5) và có véc tơ chỉ phương . Phương trình tham số của là: 
 A. 
B. 
C. 
D. Một đáp số khác. 
Câu 11:Khoảng cách từ điểm đến đường thẳng : là:
A.28
B. 
C. 
D. Một đáp án khác
Câu 12: Góc tạo bởi hai đường thẳng là:
A. 
B. 
C. 
D. 
II. PHẦN TỰ LUẬN (7điểm)
Câu 13 (2đ): Trong mpOxy cho tam giác ABC với A(6;5) B(2 ;3) và C(–2 ;–1) .
a) Tính b) Tìm trực tâm H giác ABC.
Câu 14(2đ): a) Cho tam giác ABC biết: c=14; a= 10, .Tính cạnh b;
 b) CMR:Với mọi tam giác ABC ta có: S=Rr(.sinA+sinB+sinC)
Câu 15(3đ): Cho 2 điểm A(1;4); B(3;2) và đường thẳng .
a)Viết phương trình đường thẳng AB.
b)Viết phương trình đường thẳng (d’) qua B và song song với (d).
c) Tìm trên (d) điểm C sao cho tam giác ABC cân tại C.
Họ và tên:
Lớp:
ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 10-02
Thời gian làm bài: 45 phút
I. PHẦN TRẮC NGHIỆM (3 điểm)
Câu 1: Trong các đẳng thức sau ,đẳng thức nào đúng:
A. sin1500 = 	B. cos1500 = 	C. cot1500 = D. tan1500 = 
Câu 2: Cho tam giác ABC đều cạnh a, AH là đường cao của tam giác ABC. Khi đó :
A. 	B. 	C. 	D. 
Câu 3: Cho 2 véc tơ và .Tích vô hướng .là:
A.25	B.31	C.17	D.21
Câu 4: Cho ba điểm .Tọa độ điểm E thỏa mãn: là:
A.E(-4;10) B.E(3;8) C.E(4;10) D.E(3;-8)
Câu 5: Cho tam giác ABC có b=7cm, a=10cm và . Diện tích S của tam giác ABC là:
	 C. 
Câu 6: Cho tam giác có . Bán kính đường tròn ngoại tiếp tam giác là :
A.12 B. 24 C. D
Câu 7: Cho tam giác ABC có ba cạnh là 6,8,10. Bán kính đường tròn nội tiếp tam giác ABC là : 
A. B.4 C.2 D.1
Câu8:Cho tam giác ABC với AB=12m, . Cạnh AC gần kết quả nào nhất bằng:
A.10,4 m B.10,7 m C.11m D.10,6m
Câu 9: Cho đường thẳng d có phương trình tổng quát . d có vectơ pháp tuyến là:
A. B. C. D. 
Câu 10: Cho đường thẳng qua A(6;7) và có véc tơ chỉ phương . Phương trình tham số của là: 
A. 
B. 
C. 
D. Một đáp số khác. 
 Câu 11:Khoảng cách từ điểm đến đường thẳng : là:
A.14
B. 
C. 
D. 
Câu 12: Góc tạo bởi hai đường thẳng là:
A. 
B. 
C. 
D. 
II. PHẦN TỰ LUẬN (7điểm)
Câu 13 (2đ): Trong mpOxy cho tam giác ABC với A(5 ;4) B(2 ;7) và C(–2 ;–1) .
a) Tính b) Tìm trực tâm H giác ABC.
Câu 14(2đ): a) Cho tam giác biết: c=12; b=8,. Tính cạnh a;
 b) CMR:Với mọi tam giác ABC ta có: S=2R2.sinA.sinB.sinC
Câu 15(3đ): Cho 2 điểm A(0;5); B(4;1) và đường thẳng .
a)Viết phương trình đường thẳng AB.
b)Viết phương trình đường thẳng (d’) qua B và song song với (d).
c) Tìm trên (d) điểm C sao cho tam giác ABC cân tại C.