Đề kiểm tra 1 tiết Hình 12 – Chương I

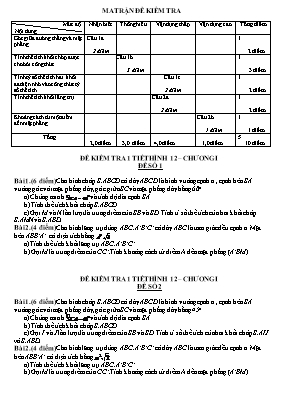
MA TRẬN ĐỀ KIỂM TRA
 Mức độ
 Nội dung
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Tổng điểm
Góc giữa đường thẳng và mặt phẳng
Câu 1a 
 2 điểm 
1
 2 điểm
Tính thể tích khối chóp được cho bởi công thức
Câu 1b 
 3 điểm
1
 3 điểm
Tính tỷ số thể tích hai khối đa diện nhờ vào công thức tỷ số thể tích 
Câu 1c
2 điểm
1
 2 điểm
Tính thể tích khối lăng trụ
Câu 2a 
 2 điểm
1
 2 điểm
Khoảng cách từ một điểm đến mặt phẳng
Câu 2b 
 1 điểm
1
 1 điểm
 Tổng
 2,0 điểm
3,0 điểm
 4,0 điểm
 1,0 điểm
5
 10 điểm
ĐỀ KIỂM TRA 1 TIẾT HÌNH 12 – CHƯƠNG I 
 ĐỀ SỐ 1
Bài 1. (6 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SC và mặt phẳng đáy bằng 600.
 a) Chứng minh và tính độ dài cạnh SA.
 b) Tính thể tích khối chóp S.ABCD.
 c) Gọi M và N lần lượt là trung điểm của SB và SD. Tính tỉ số thể tích của hai khối chóp S.AMN và S.ABD.
Bài 2. (4 điểm) Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Mặt bên ABB’A’ có diện tích bằng .
 a) Tính thể tích khối lăng trụ ABC.A’B’C’. 
 b) Gọi M là trung điểm của CC’.Tính khoảng cách từ điểm A đến mặt phẳng (A’BM)
ĐỀ KIỂM TRA 1 TIẾT HÌNH 12 – CHƯƠNG I 
ĐỀ SỐ 2
Bài 1. (6 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SC và mặt phẳng đáy bằng 450.
 a) Chứng minh và tính độ dài cạnh SA.
 b) Tính thể tích khối chóp S.ABCD.
 c) Gọi I và J lần lượt là trung điểm của SB và SD. Tính tỉ số thể tích của hai khối chóp S.AIJ và S.ABD.
Bài 2. (4 điểm) Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Mặt bên ABB’A’ có diện tích bằng .
 a) Tính thể tích khối lăng trụ ABC.A’B’C’. 
 b) Gọi M là trung điểm của CC’.Tính khoảng cách từ điểm A đến mặt phẳng (A’BM)
ĐÁP ÁN VÀ THANG ĐIỂM– ĐỀ 1 
Câu
Đáp án
Điểm
Câu
Đáp án
Điểm
1a
(2,0đ)
SA ^ (ABCD) Þ AC là hình chiếu của SC trên mp(ABCD).
Þ là góc giữa SC và mp(ABCD)
Þ 
 -----------------------------------------
Tam giác SAC vuông tại A 
0,50
0,25
0,25
------
0,25
0,25
0,25
0,25
2a
(3,0đ)
ABB’A’ là hình chữ nhật 
0,50
0,50
0,50
0,50
0,50
0,50
1b
(3,0đ)
1.00
1,00
0,50
0,50
2b
(1đ)
Gọi N, P lần lượt là trung điểm của A’B, AB Þ MNPC là hình chữ nhật Þ MN // CP 
Ta có CP ^ AB và CP ^ AA’
Þ CP ^ (A’AB) Þ MN ^ (A’AB)
Kẻ AH ^ A’B ( H Î A’B), ta có
MN ^ (A’AB) Þ AH ^ MN 
Þ AH ^ (A’BM)
Þ AH = d(A, (A’BM))
0,25
0,25
1c
(1,0đ)
M là trung điểm của SB Þ 
N là trung điểm của SD Þ 
0,25
0,25
0,25
0,25
Tam giác A’AB vuông tại A
0,25
0,25
Ghi chú : Nếu HS làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm từng phần.
ĐÁP ÁN VÀ THANG ĐIỂM – ĐỀ 2 
Câu
Đáp án
Điểm
Câu
Đáp án
Điểm
1a
(2,0đ)
SA ^ (ABCD) Þ AC là hình chiếu của SC trên mp(ABCD).
Þ là góc giữa SC và mp(ABCD)
Þ 
 -----------------------------------------
Þ Tam giác SAC vuông cân tại A 
0,50
0,25
0,25
------
0,50
0,25
0,25
2a
(3,0đ)
ABB’A’ là hình chữ nhật 
0,50
0,50
0,50
0,50
0,50
0,50
1b
(3,0đ)
1.00
1,00
0,50
0,50
2b
(1đ)
Gọi N, P lần lượt là trung điểm của A’B, AB Þ MNPC là hình chữ nhật Þ MN // CP 
Ta có CP ^ AB và CP ^ AA’
Þ CP ^ (A’AB) Þ MN ^ (A’AB)
Kẻ AH ^ A’B ( H Î A’B), ta có
MN ^ (A’AB) Þ AH ^ MN 
Þ AH ^ (A’BM)
Þ AH = d(A, (A’BM))
0,25
0,25
1c
(1,0đ)
I là trung điểm của SB Þ 
J là trung điểm của SD Þ 
0,25
0,25
0,25
0,25
Tam giác A’AB vuông tại A
0,25
0,25