Đề kiểm tra 1 tiết Giải tích 12 - Mã đề 109

SỞ GIÁO DỤC - ĐÀO TẠO KHÁNH HÒA
ĐỀ KIỂM TRA 1 TIẾT GIẢI TÍCH 12 
(M· ®Ò 109)
TRƯỜNG ISCHOOL NHA TRANG
Thời gian: 45 phút , không kể thời gian phát đề
C©u 1 : 
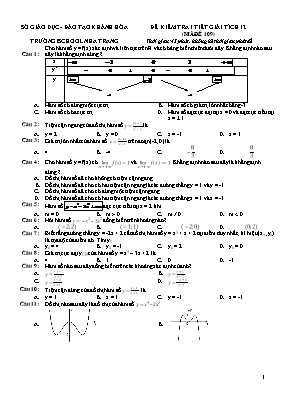
Cho hàm số y = f(x) xác định và liên tục trên R và có bảng biến thiên dưới đây. Khẳng định nào sau đây là khẳng định đúng ?
x
y’
y
-4
-4
A.
Hàm số có đúng một cực trị.
B.
Hàm số có giá trị lớn nhất bằng -3
C.
Hàm số có ba cực trị.
D.
Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = ± 1.
C©u 2 : 
Tiệm cận ngang của đồ thị hàm số y=2x+1x2-1 là
A.
y = 2.
B.
y = 0.
C.
x = -1.
D.
x = 1.
C©u 3 : 
Giá trị lớn nhất của hàm số y=4-2xx-1 trên đoạn [-2;0] là
A.
4
B.
-4
C.
-83
D.
83
C©u 4 : 
Cho hàm số y = f(x) có limx→+∞fx=1 và limx→+∞fx=-1. Khẳng định nào sau đây là khẳng định đúng ?
A.
Đồ thị hàm số đã cho không có tiệm cận ngang.
B.
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1 và y = -1.
C.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D.
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 1 và x = -1.
C©u 5 : 
Hàm số đạt cực tiểu tại x = 2 khi
A.
m = 0
B.
m > 0
C.
m ≠ 0
D.
m < 0
C©u 6 : 
Hỏi hàm số y=-x3-3x2 đồng biến trên khoảng nào?
A.
(-2;2)
B.
(-1;1)
C.
(-2;0)
D.
(0;2)
C©u 7 : 
Biết rằng đường thẳng y = -2x + 2 cắt đồ thị hàm số y = x3 + x + 2 tại điểm duy nhất ; kí hiệu (x0 ;y0) là tọa độ của điểm đó. Tìm y0.
A.
y0 = 4.
B.
y0 = -1.
C.
y0 = 2.
D.
y0 = 0.
C©u 8 : 
Giá trị cực đại yCĐ của hàm số y = x3 – 3x + 2 là
A.
4.
B.
1.
C.
0.
D.
-1.
C©u 9 : 
Hàm số nào sau đây đồng biến trên các khoảng xác định của nó?
A.
y=-x-1x+2 .
B.
y=x+1x-2 .
C.
y=x-2x+1 .
D.
y=-x+2x-1 .
C©u 10 : 
Tiệm cận đứng của đồ thị hàm số y=x-1x+1 là
A.
y = 1.
B.
x = 1.
C.
y = -1.
D.
x = -1.
C©u 11 : 
Đồ thị nào sau đây là đồ thị của hàm số y=x4-2x2
A.
B.
C.
D.
C©u 12 : 
Hỏi hàm số y=14x4-2x2 nghịch biến trên các khoảng nào ?
A.
(-∞;-2) và (2;+∞)
B.
(-∞;-2) và (0;2)
C.
(0;2) và (2;+∞)
D.
(-2;0) và (2;+∞)
C©u 13 : 
Giá trị cực tiểu yCT của hàm số y=-12x4+14x2 bằng
A.
132
B.
0
C.
-12
D.
12
C©u 14 : 
Đồ thị nào sau đây là đồ thị của hàm số =x3+3x2 ?
A.
B.
C.
D.
C©u 15 : 
Tìm giá trị nhỏ nhất của hàm số y=x2+3x-1 trên đoạn [2 ;4].
A.
min[2;4]y=193
B.
min[2;4]y=-3
C.
min[2;4]y=6
D.
min[2;4]y=-2
C©u 16 : 
Hình dưới đây là đồ thị của hàm số y=x3-6x2+9x. Dựa vào đồ thị đã cho, hãy tìm m sao cho phương trình x3-6x2+9x-m=0 có 1 nghiệm duy nhất
A.
-4<m<0
B.
m4	
C.
m0
D.
0<m<4
C©u 17 : 
Cho các hàm số (1): y=x3+x; (2): y=x4+x2; (3): y=x+1x-1; (4): y=x2+1x-1. Trong các hàm số trên, những hàm số nào không có cực trị?
A.
(1) và (3)
B.
(1) và (2)
C.
(2) và (4)
D.
(3) và (4)
C©u 18 : 
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm giao điểm của đồ thị hàm số với trục tung bằng:
A.
2
B.
-2
C.
-1
D.
1
C©u 19 : 
Phương trình tiếp tuyến của đồ thị hàm số y = x3 – 3x2 + 1 tại điểm có hoành độ bằng 2 là :
A.
y = -2
B.
y = 2
C.
y = 3
D.
y = -3
C©u 20 : 
Giá trị nhỏ nhất của hàm số y=x4+3x2-5 là
A.
0
B.
5
C.
-1
D.
-5
phiÕu soi - ®¸p ¸n (Dµnh cho gi¸m kh¶o)
M«n : KIEM TRA 1 TIET GIAI TICH CHUONG I
M· ®Ò : 109
01
{ | } )
D
02
{ ) } ~
B
03
{ | ) ~
C
04
{ ) } ~
B
05
) | } ~
A
06
{ | ) ~
C
07
{ | ) ~
C
08
) | } ~
A
09
{ | ) ~
C
10
{ | } )
D
11
{ | } )
D
12
{ ) } ~
B
13
{ ) } ~
B
14
) | } ~
A
15
{ | ) ~
C
16
{ ) } ~
B
17
) | } ~
A
18
) | } ~
A
19
{ | } )
D
20
{ | } )
D