Đề kiểm tra 1 tiết chương chương 3 Hình học 9

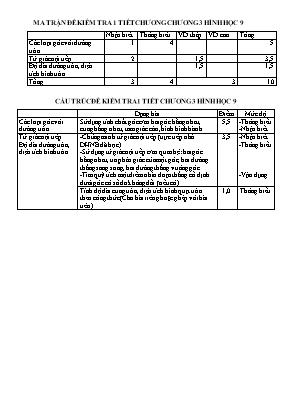
MA TRẬN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG CHƯƠNG 3 HÌNH HỌC 9
Nhận biết
Thông hiểu
VD thấp
VD cao
Tổng
Các loại góc với đường tròn
1
4
5
Tứ giác nội tiếp
2
1,5
3,5
Độ dài đường tròn, diện tích hình tròn
1,5
1,5
Tổng
3
4
3
10
CẤU TRÚC ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3 HÌNH HỌC 9
Dạng bài
Điểm
Mức độ
Các loại góc với đường tròn
Sử dụng tính chất góc c/m hai góc bằng nhau, cung bẳng nhau, tam giác cân, hình bình hành....
5,5
-Thông hiểu
-Nhận biết
Tứ giác nội tiếp
Độ dài đường tròn, diện tích hình tròn
-Chứng minh tứ giác nội tiếp (trực tiếp nhờ DHNB đã học).
-Sử dụng tứ giác nội tiếp c/m quan hệ: hai góc bằng nhau, tia phân giác của một góc, hai đường thẳng song song, hai đường thẳng vuông góc.....
-Tìm quỹ tích một điểm nhìn đoạn thẳng cố định dưới góc có số đo không đổi (nếu có)
3,5
-Nhận biết
-Thông hiểu
-Vận dụng
Tính độ dài cung tròn, diện tích hình quạt tròn theo công thức (Cho bài riêng hoặc ghép với bài trên)
1,0
Thông hiểu
UBND QUẬN LÊ CHÂN
TRƯỜNG THCS VÕ THỊ SÁU
ĐỀ CHÍNH THỨC 
ĐỀ KIỂM TRA CHƯƠNG III
MÔN: HÌNH HỌC 9
(Thời gian làm bài: 45 phút) 
Ngày 16/3/2017
Bài 1: (5, 5 điểm)
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm D và vẽ đường tròn tâm O đường kính CD, BC cắt đường tròn tại E, BD cắt đường tròn tại F.
a/ Chứng minh tứ giác ABED nội tiếp.
b/ Chứng minh .
c/ Chứng minh AC là tia phân giác của góc EAF.
d/ Biết , CD = 4cm. Tính diện tích hình quạt tròn DOE. (ứng với cung nhỏ DE của đường tròn (O))
Bài 2 (4, 5 điểm).
Cho DMNP nhọn nội tiếp đường tròn tâm O, hai đường cao hạ từ hai đỉnh M và N cắt nhau tại H và cắt đường tròn lần lượt tại D và E.
a/ Chứng minh PD = PE.
b/ Chứng minh DDNH cân.
c/ Gọi I là trung điểm PN. So sánh độ dài OI và MH.
-------------------Hết-------------------
ĐÁP ÁN VÀ CHO ĐIỂM
Bài
Đáp án
Điểm
Bài 1
0,5
a/ Ta có (góc nội tiếp chắn nửa đường tròn) Þ(kề bù với góc )
Tứ giác ABED có 
0,25
0,5
0,25
0,5
b/ Tứ giác ABED nội tiếp Þ(cùng bù với )
(đpcm)
1,0
c/ Tứ giác ABCF có 2 đỉnh A và F cùng nhìn cạnh BC dưới góc 900 nên ABCF nội tiếp Þ (2 góc nội tiếp cùng chắn cung FC).
Lại có (2 góc nội tiếp cùng chắn cung DE).
Suy ra . Vậy AC là tia phân giác của góc EAF.
0,5
0,25
0,75
 d/ Þsđ , bán kính R của đường tròn (O) là 2cm.
Áp dụng công thức tính diện tích hình quạt tròn, ta có
SquạtDOE = (cm2)
0,25
0,75
Bài 2
0,5
a/ Có và mà (đối đỉnh) Þ 
Xét đường tròn (O) có (cmt) Þ (đpcm)
0,75
0,75
b/ Vì 
Xét DNHD có NP là đường cao đồng thời là đường phân giác nên DNHD cân tại N (đpcm)
0,5
1,0
c/ Kẻ đường kính MM’.
HS c/m được tứ giác PHNM’ là hình bình hành
Suy ra I là trung điểm của HM’
Xét DMHM’ có OI là đường trung bình của tam giác nên .
0,25
0,25
0,5
UBND QUẬN LÊ CHÂN
TRƯỜNG THCS VÕ THỊ SÁU
ĐỀ CHÍNH THỨC 
ĐỀ KIỂM TRA CHƯƠNG III
MÔN: HÌNH HỌC 9
(Thời gian làm bài: 45 phút) 
Ngày 20/3/2017
Bài 1 (4, 0 điểm). 
Cho đường tròn tâm O bán kính R = 2cm, cung AmB có số đo bẳng 600.
a/ Tính sđ .
b/ Tính độ dài cung AmB.
c/ Tính diện tích hình quạt tròn OAmB.
d/ Tính diện tích hình viên phân giới hạn bởi dây AB và cung AmB.
Bài 2 (6, 0 điểm).
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm D (D khác A và C), kẻ DE vuông góc với BC.
a/ Chứng minh tứ giác ABED nội tiếp.
b/ Chứng minh .
c/ Đường thẳng BD cắt đường tròn đường kính DC tại F. Chứng minh 4 điểm A, B, C, F cùng nằm trên một đường tròn.
d/ Chứng minh D là tâm đường tròn nội tiếp tam giác AEF.
--------------Hết--------------
ĐÁP ÁN VÀ CHO ĐIỂM
Bài
Đáp án
Điểm
Bài 1
(4đ)
a/ số đo cung AmB = 
Þ số đo cung AnB = 3600 – 600 = 3000
b/ Độ dài cung AmB = 
c/ Diện tích hình quạt tròn OAmB = 
0,5
0,5
1, 0
1, 0
d/ -Tam giác AOB đều (OA = OB và ) cạnh 2cm nên có diện tích bằng 
-Diện tích hình viên phân = diện tích hình quạt tròn OAmB – diện tích tam giác AOB = .
0,25
0,75
Bài 2
(6đ)
0,5
a/ Tứ giác ABED có , (đề bài cho)
Þ, mà 2 góc này đối nhau 
Þ Tứ giác ABED nội tiếp (DHNB) (đpcm).
0,5
0,75
0,25
b/ Tứ giác ABED nội tiếp Þ mà (2 góc kề bù) Þ(đpcm).
1, 0
0,5
c/ Vì điểm E thuộc đường tròn đường kính DC nên 
Như vậy 2 điểm A và F cùng nhìn cạnh BC dưới một góc bằng 900 suy ra 4 điểm A, B, C, F thuộc đường tròn đường kính BC (đpcm). 
0,5
1,0
d/ Tứ giác ABCF nội tiếp Þ(2 góc nội tiếp cùng chắn cung CF).
+Tứ giác ABED nội tiếp Þ(2 góc nội tiếp cùng chắn cung DE). Do đó ÞAC là phân giác của góc EAF.
+Chứng minh tương tự, ta cũng có ED là phân giác của góc AEF Vậy D là tâm đường tròn nội tiếp DAEF(đpcm)
0,5
0,25
0,25