Đề kiểm tra 1 tiết chương 1 hình 8 năm học 2015 - 2016 thời gian làm bài 45 phút

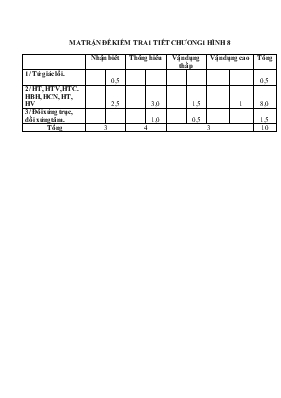
MA TRẬN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1 HÌNH 8
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Tổng
1/ Tứ giác lồi.
0,5
0,5
2/ HT, HTV, HTC. HBH, HCN, HT, HV
2,5
3,0
1,5
1
8,0
3/ Đối xứng trục, đối xứng tâm.
1,0
0,5
1,5
Tổng
3
4
3
10
UBND QUẬN LÊ CHÂN
TRƯỜNG THCS VÕ THỊ SÁU
ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1 HÌNH 8
NĂM HỌC 2015 - 2016
Thời gian làm bài 45 phút
(không tính thời gian giao đề)
Bài 1(3, 0 điểm): 
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA.
a/ Chứng minh tứ giác EFGH là hình bình hành.
b/ Tìm điều kiện của tứ giác ABCD để EFGH là hình chữ nhật
Bài 2 (1,5 điểm) : 
 Tìm số đo các góc của tứ giác ABCD trong hình vẽ dưới đây (x là số đo góc).
Bài 3 (5, 5 điểm): 
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, E là điểm đối xứng với H qua AC.
a/ Chứng minh rằng A là trung điểm của DE.
b/ Tam giác DHE là tam giác gì ? Vì sao ?
c/ Chứng minh tứ giác BCDE là hình thang và tính diện tích của tứ giác BDEC khi BC = 5cm, AH = 2cm.
-----------------------Hết----------------------
ĐÁP ÁN VÀ CHO ĐIỂM
Bài
Đáp án
Điểm
Bài 1
(3, 0 điểm): 
a/ Theo đề bài ta có HE là đường trung bình của DABD ÞHE // BD và 
GF là đường trung bình của DCBD ÞHE // BD và .
Do đó HE // GF và HE = GF nên tứ giác EFGH là hình bình hành.
0,5
0,5
0,5
0,5
b/ EFGH là hình chữ nhật Þ HE ^EF, mà HE// BD và HF // AC suy ra AC ^BD.
Vậy ABCD có AC ^BD thì EFGH là hình chữ nhật
0,5
0,5
Bài 2 
(1,5 điểm) : 
Ta có x + 2x + 3x + 4x = 3600 (Tổng các góc của 1 tứ giác) 
Þ10x = 3600 Þx = 360
Vậy 
0,5
0,5
0,5
Bài 3 
(5, 5 điểm): 
vẽ hình đúng cho câu a/
0,5
 a/ Vì D đối xứng với H qua AB, E đối xứng với H qua AC nên , 
mà 
do đó D, A, E thẳng hàng (1)
Cũng vì D đối xứng với H qua AB, E đối xứng với H qua AC nên AD = AH và AE = AH ÞAD = AE (2) 
Từ (1) và (2) suy ra A là trung điểm của DE 
0,5
0,5
0,5
0,5
b/ Tam giác DHE có HA = AD = AE = nên vuông tại H.
1, 5
c/ Có DADB = DAHB (AB chung ; AD = AH; ) ÞBD = BH. 
DAEC = DAHC (AC chung ; AE = AH; ) ÞCE = CH .
Vậy BC = BH + CH = BD + CE (đpcm)
0,5
0,5
0,5